Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделі некооперованої олігополіїСодержание книги
Поиск на нашем сайте Розглянемо моделі некооперованої олігополії ґрунтуючись на моделях кількісної олігополії Курно і Штакельберга. Як відомо, історично першим змоделював взаємовідносини двох фірм за умов олігополії ще в 30-х роках ХІХ ст. французький економіст Антуан Курно. Він вважається фундатором теорії олігополії. Модель Курно пояснює як здійснюють вибір обсягу виробництва два олігополісти, що мають приблизно однакові економічні можливості і виробляють однорідну продукцію. Приймаючи рішення щодо обсягу виробництва кожне підприємство враховує реакцію свого конкурента. Вважається, що обидва олігополісти приймають рішення одночасно і самостійно за умови відомого ринкового попиту. Суть моделі Курно полягає в тому, що кожен виробник розглядає рівень виробництва конкурента як фіксований, а потім вирішує, скільки ж виробляти самому, аби максимізувати прибуток. Проведемо аналітичне доведення рівноваги Курно. При функції ринкового попиту:
де Q – обсяг ринкового попиту. При
де Q1 – обсяг виробництва І виробника; Q2 – обсяг виробництва ІІ виробника.
Прибуток першого виробника можна визначити як різницю між його доходом і витратами, тобто:
де С – витрати на одиницю продукції. Підставивши в праву частину рівняння (11.11) значення Р, отримаємо:
Прибуток буде досягати максимуму, коли перша похідна функції дорівнює нулю:
Звідки витікає, що для отримання максимального прибутку перше підприємство має виробляти обсяг продукції Q 1:
Рівняння (11.14) є характеристикою реакції першого виробника на обсяг виробництва його конкурента і називається рівнянням реакції першого виробника на дії другого. За лінійних функцій попиту і витрат обсяг пропозиції дуополіста менший від обсягу пропозицій монополії, яка максимізує свій прибуток, на половину обсягу пропозиції його конкурента. Аналогічні дії дають можливість одержати рівняння реакції другого виробника на дії першого:
Побудовані лінії реакції
Рис. 11.5. Рівновага дуополії Курно
Q1p i Q2p – обсяги індивідуальної пропозиції виробників, у зміні яких не зацікавлений жоден із конкурентів. Аналітично обсяг Q1p одержимо, якщо в рівняння (11.14) підставимо рівняння (11.15):
Аналогічно рівноважний обсяг пропозиції другого виробника:
Ринкова пропозиція:
Підставивши значення Q 1 i Q 2 у функцію галузевого попиту знайдемо ціну рівноваги:
Таким чином, за умов рівноваги кожен з дуополістів максимізує свій прибуток, забезпечуючи своєю продукцією третину ринкового попиту за єдиною ціною. Рівноважні обсяги дуополістів Q 1p і Q 2p є координатами точки рівноваги обсягів Курно-Неша. Рівновага за Нешем репрезентується ситуацією, коли кожен виробник у взаємодії з рештою учасників обирає оптимальний варіант поведінки за умов, що решта учасників ринку дотримується певної стратегії. Рівновага Курно є окремим випадком рівноваги Неша. Тут стратегія олігополіста спрямована на вибір оптимального обсягу виробництва, а не ціни. Незважаючи на простоту і легкість побудови, модель Курно не позбавлена недоліків. Зокрема, малоймовірним є обрання незмінного обсягу випуску продукції впродовж тривалого періоду та ще й за умов неповного задоволення ринкового попиту. Однак олігополія в моделі Курно є більш ефективною, аніж рівновага за умов таємної змови, хоча і в свою чергу є гіршою, ніж рівновага конкурентного ринку. Розвиток моделі кількісної дуополії Курно призвів до моделі асиметричної дуополії, яку у 1934 році запропонував Г. фон Штакельберг. Асиметрія дуополії Штакельберга полягає в тому, що дуополісти схильні дотримуватись різних типів поведінки. Вони або прагнуть бути лідерами, або залишатися аутсайдерами. Модель Штакельберга описує поведінку конкурентів, які мають неоднакову економічну силу і сильніший прагне скористатися роллю лідера ринку. Олігополіст за моделлю Штакельберга дотримується припущення Курно, діє відповідно до своєї кривої реагування і приймає рішення про випуск продукції, що максимізує його прибуток, вважаючи обсяг виробництва конкурента заданим. Лідер, знаючи функцію, що описує криву реагування послідовника – аутсайдера, вводить її в свою функцію прибутку, що дає йому змогу отримувати максимальний прибуток. Якщо бізнесова поведінка обох виробників не змінюється, один – лідер, другий – аутсайдер, то на ринку не виникає конфлікту і результат їх взаємодії стабільний, передбачуваний. Якщо ж обидва дуополісти намагаються стати лідерами, то це стане передумовою розв’язання цінової війни. Вона триватиме до тих пір, поки хоча б один з дуополістів не відмовиться від намагання стати лідером або обидва вдадуться до змови. За Штакельбергом – останній спосіб розв’язання ситуації найбільш ймовірний. Проте стратегія олігополіста може полягати і у виборі іншого параметра, наприклад, ціни. Поведінку дуополіста при стратегічній змінній ціні описує модель цінової олігополії. Її можна аналізувати ґрунтуючись на моделі цінової олігополії Бертрана. В моделі Курно ми припускали, що фірми обирають обсяги виробництва, а ринок визначає ціну. Модель французького економіста Жозефа Бертрана, розроблена в 1883 році передбачає, що олігополіст визначає ціну на свою продукцію за прийнятих умов щодо цін, які оберуть інші виробники. Кожний учасник ринку обирає такі ціни, які дають йому можливість отримати максимальний прибуток за даної ціни конкурента. Якщо фірми продають ідентичну продукцію, то умова рівноваги у моделі Бертрана буде збігатися з умовою конкурентної рівноваги (Р = МС). Адже, якщо ціна буде перевищувати граничні витрати (P > MC), конкуренти матимуть потужні стимули зниження своєї ціни, аби не втратити своєї ринкової квоти. Врешті-решт, за рівних граничних витрат конкурентів рівновага на ринку настане, коли граничні витрати виробників зрівняються з ринковою ціною і зникне потреба подальшого зниження ціни. Отож, за будь-якої ціни, що є вищою за граничні витрати, ринкової рівноваги існувати не може. Спрощений варіант моделі Бертрана подано на рис. 11.6.
Рис. 11.6. Модель Бертрана. Рівновага в олігополії
Кожен з рівних за економічною силою олігополістів характеризується власною функцією реагування, яка відображає всі зниження ціни, які за очікуваної ціни його конкурента забезпечать отримання максимального прибутку (Р 1=ƒ(Р 2); Р 2=ƒ(Р 1). Зазначимо, що обидві криві реагування є висхідними. Це означає, що ціни дуополістів Бертрана мають чітко виражену тенденцію до наближення. Якщо перший олігополіст встановить ціну, яка відповідає його намаганням одержати максимальний прибуток, другий відреагує на це встановленням своєї ціни. Це викличе реакцію пристосування першого олігополіста. Процес взаємного пристосування триватиме до тих пір, поки не встановиться рівновага, наприклад, у точці Е (Р1P; Р2P). Така рівноважність є стійкою тому, що обидві фірми зійдуться на однаковій ціні (Р1P = Р2P). Якщо враховувати витрати виробництва, то стійка рівновага досягатиметься якраз у стані конкурентної рівноваги, а саму модель можна розглядати як формалізований сценарій певної цінової війни. Рівновага Бертрана, як і рівновага Курно є різновидами більш загального поняття теорії ігор-рівноваги Неша. За рівноваги Бертрана-Неша, кожен олігополіст повністю реалізує свій потенціал, приймаючи ціну конкурента як задану.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.01 с.) |

 (11.9)
(11.9) , отримаємо:
, отримаємо: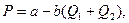 (11.10)
(11.10) (11.11)
(11.11)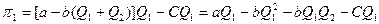 (11.12)
(11.12)

 (11.13)
(11.13) (11.14)
(11.14) (11.15)
(11.15) і
і  (рис. 11.5) дуополістів визначають ринкову рівновагу (т.Е).
(рис. 11.5) дуополістів визначають ринкову рівновагу (т.Е).

 ;
;  ;
;  (11.16)
(11.16) (11.17)
(11.17) (11.18)
(11.18)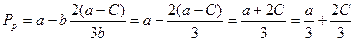 (11.19)
(11.19)