
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление массива значений функцииСодержание книги
Поиск на нашем сайте Весьма распространенной задачей является создание массива значений некоторой заданной функции f(x) на заданном отрезке изменения аргумента xн < x < xк (от x–начального до x–конечного) с заданным шагом D x = h. Такая задача возникает в случаях приближенного вычисления интегралов, поиска локальных экстремумов функции, ее наибольших и наименьших значений, численного решения уравнений и т.п. Иногда одновременно с массивом значений функции необходимо иметь и массив соответствующих значений аргумента. Рассмотрим программную реализацию данной задачи на конкретном примере, который без труда может быть обобщен на любые другие уравнения функций, величин отрезков и шагов. Пример 3.1 Пусть необходимо создать массивы значений аргумента x и функции y для функции
на отрезке 0 Отметим прежде всего, что количество элементов массива в таком случае вычисляется по формуле
где хн и хк – начальное и конечное значения аргумента. В данном случае n= Последовательные значения аргумента X удобно вычислять по формуле Xi = Xн + h (i – 1). Фрагмент программы, реализующей поставленную задачу, может быть оформлен следующим образом: program Masfun; type mas= array [1..25] of real; var x,y:mas; i:integer; Begin for i:=1 to 25 do Begin x[i] = 0 + 0.25*(i–1); y[i] = 2*exp(1.5*x[i])*cos(x[i]/2–0.5); writeln('x=';x[i]:5:2;' y=';y[i]:6:3) end; end. СУММИРОВАНИЕ И ПЕРЕМНОЖЕНИЕ ЭЛЕМЕНТОВ МАССИВОВ Рассмотрим задачу нахождения суммы и произведения всех элементов некоторого одномерного массива X т.е. пусть дано X1,X2,... Xk,... Xn и требуется вычислить: S = X1 + X2 +... + Xk +...+ Xn; P = X1 * X2 *... * Xk *...* Xn. Из математической формулировки задачи вытекает и алгоритм вычисления суммы: присваиваем сумме значение первого слагаемого, а затем наращиваем эту величину последовательным прибавлением к ней каждого очередного слагаемого, начиная со второго и кончая последним. Делать это следует, разумеется, в цикле. Таким образом сумма может быть вычислена фрагментом из двух операторов: S:= X[1]; for k:= 2 to n do S:= S + x[k]; Аналогично вычисляется и произведение: P:= x[1]; for k:= 2 to n do P:= P * x[k]; Во многих случаях, однако, более удобно начинать вычисление суммы и произведения с присвоения им первоначально, соответственно нулевого и единичного значений, после чего наращивание суммы и произведения начинать с первого элемента массива, т.е. одновременное вычисление величин S и P может быть в данном случае выполнено и так: S:=0;P:=1; for k:=1 to n do Begin S:= S + x[k]; P:= P * x[k]; end; При суммировании и перемножении элементов двумерных массивов – матриц требуется перебирать все элементы по рядам: либо по строкам и в каждой строке по столбцам, либо по столбцам и в каждом столбце по строкам. Например вычислить сумму и произведение всех элементов матрицы A размером m * n (см. пример 2.9) можно с помощью следующих операторов: S:=0; P:=1; for i:=1 to m do Begin for j:=1 to n do Begin S:= S + a[i,j]; P:= P * a[i,j]; end; end; Результат не изменится, если в данном фрагменте операторы циклов по i и j поменять местами. Рассмотрим еще одну задачу, довольно часто встречающуюся в работе с массивами. Пусть дано два одинаковых по размеру массива X и Y (i=1,2,...n). Требуется вычислить величину SP = x1 y1 + x2 y2 +... + xi yi +... + xn yn. Отметим, что такая сумма – сумма попарных произведений одноименных элементов двух массивов (векторов) называется скалярным произведением этих массивов. Вычисление этого произведения может быть выполнено так: SP:= 0; for i:=1 to n do SP:= SP + x[i]*y[i]; ТИПОВЫЕ ЗАДАЧИ ОБРАБОТКИ МАССИВОВ Все виды задач обработки массивов сводятся к сочетаниям циклических и разветвляющихся вычислительных процессов и представляют собой разветвления в циклах или циклы в разветвлениях. Задачи выборок Задачи выборок могут ставиться по разному, но в общем случае сводятся к выбору из данного массива элементов с заданными свойствами или по заданному признаку. Пример 5.1. Дан массив mz месячных заработков сотрудников предприятия (i=1,2,...n). Пусть p – процентная ставка подоходного налога, который вычитается из суммы заработка: при mz < z1 p = p1; при z1 при mz Рассчитать сумму подоходного налога sn и сумму причитающейся получки sp каждого сотрудника. Задача, очевидно, сводится к просмотру всего массива заработков и выбору из него сумм, попадающих в пределы: < z1; от z1 до z2; > z2, после чего суммы налогов и получки вычисляются по формулам sn = mz * p/100 и sp = mz – sn. где p принимает значения p1, p2, p3 в зависимости от величины mz. Соответствующий фрагмент программы в предположении, что массив mz и константы n, z1, z2, z3, p1, p2, p3 введены, может иметь вид for i:=1 to n do Begin if mz[i]<z1 then p:=p1; if mz[i]>=z1 and mz[i]<z2 then p:=p2; if mz[i]>=z2 then p:=p3; sn:= mz[i]*p div 100; sp:=mz[i] – sn; write(i:2,' Заработок ',mz[i]:6,' Налог ',sn:6,' Получка ',sp:6); end; Аналогично выполняется и выборка элементов двумерных массивов. Пример 5.2. В двумерном массиве p размером 6? 8 выбрать все отрицательные числа, вывести их и подсчитать их общее количество. Если искомое количество отрицательных элементов обозначить k, то соответствующий фрагмент программы может иметь вид: k:=0; for i:=1 to 6 do Begin for j:=1 to 8 do Begin if p[i,j]<0 then Begin k:=k+1; write(p[i,j]); end; end; end; write(' Число отрицательных элементов k=',k); 5.2 Преобразование одних массивов в другие Задачи этого типа тесно связаны с задачами выборок и суть их легко понять из рассмотрения соответствующих примеров. Пример 5.3. Пусть rsbi – рейтинговая сумма балов i–го студента за 1–й этап обучения (i=1..n). Студенты, набравшие сумму балов, не менее некоторой контрольной ks, образуют элитную группу и могут быть переведены на 2–й этап обучения. Допустим требуется проанализировать средние показатели успеваемости элитной и остальной групп по отдельности. Это означает, что общий массив rsb необходимо разделить на 2 массива rse и rso, отобрав в первый из них суммы балов program Rejting; Const n=150; ks=4800; Type mas= array [1..n] of integer; Var rsb,rse,rso:mas;i,j,k:integer; Begin { ввод массива rsb } j:=0; k:=0; for i:=1 to n do Begin if rsb[i]>=ks then Begin j:=j+1; rse[j]:=rsb[i]; End Else Begin k:=k+1; rso[k]:=rsb[i]; end; end; writeln(' Элитный массив '); for i:=1 to j do write(rse[i]:8); writeln; writeln(' Остальной массив'); for i:=1 to k do write(rso[i]:8); end. Рассмотрим аналогичный пример с двумерным массивом. Пример 5.4. В матрице А(10х10) выбрать числа больше 8 и меньше 2 и сформировать из них два одномерных массива – вектора B и C. Ниже приводится фрагмент программы в котором исходная пробная матрица формируется с помощью функции Random (см. раздел 2.2).Единственное, что требует пояснения в данном случае. это заказ количества элементов в описании формируемых массивов B и C. Оно, очевидно, должно указываться как и в предыдущем примере с "запасом", на случай, если все элементы матрицы попадут в один или другой массив B или C, т.е. должно быть равно 100. program MatrVec; Type vec= array [1..100] of real; Var a: array [1..10,1..10] of real; b,c:vec; i,j,k,l:integer; Begin writeln(' Исходная матрица '); for i:=1 to 10 do Begin for j:=1 to 10 do Begin a[i,j]:=9.999*Random; write(a[i,j]:5:2); end; writeln; end; k:=0; i:=0; for i:=1 to 10 do Begin for j:=1 to 10 do Begin if a[i,j]>8 then Begin k:=k+1; b[k]:=a[i,j]; End else if a[i,j]<2 then Begin l:=l+1; c[l]:=a[i,j]; end; end; end; writeln(' Вектор B '); for i:=1 to k do write(b[i]:5:2); writeln(' Вектор C'); for i:=1 to l do write(c[i]:5:2); end. К задачам преобразования массивов относятся и задачи слияния нескольких однородных массивов в один. Пример 5.5. Пусть, например, в эксперименте выполнено 3 серии измерений некоторой величины X. При этом в первой серии выполнено 25 измерений, во второй 30 и в третьей 15. Иными словами, получено 3 массива данных: X1 (i=1..25); X2 (i=1..30) и X3 (i=1..15). Требуется объединить три массива в один общий массив X, расположив в нем сначала элементы массива X1, затем X2, затем X3 и обеспечив общую сквозную нумерацию элементов массива X (i=1..70). В этом случае, очевидно, 25 первых элементов массива X совпадут с одноименными элементами массива X1, то есть перенумеровка элементов массива X1 в элементы массива X будет выполняться по формуле Xi = X1i (i=1..25). Затем первый элемент массива X2 должен стать 26–м элементом массива X и т.д. То есть каждый i–й элемент массива X2 должен переименоваться в 25+i –й элемент массива X. Иными словами, перенумеровка элементов массива X2 в элементы массива X должна выполняться по формуле X25+i= X2i (i=1..30). В конце этого цикла очевидно получим X55 = X230. Далее, первый элемент массива X3 должен стать 56–м элементом массива X и, рассуждая аналогично предыдущему, получим, что перенумеровка элементов массива X3 в элементы массива X должна выполняться по формуле X55+i = X3i (i=1..15). Соответствующий фрагмент программы слияния массивов, реализующий данный алгоритм представлен ниже. Отметим, что в данном случае описания всех четырех массивов целесообразно выполнить в разделе Type, заказав для каждого из них размер наибольшего, а именно массива X, включающего суммарное количество 70 элементов. program SliMas; Type vec= array [1..70] of real; Var X1,X2,X3,X:vec; i:integer; Begin Begin { ввод массивов X1,X2,X3 } end; Begin for i:=1 to 25 do X[i]:=X1[i]; for i:=1 to 30 do X[25+i]:=X2[i]; for i:=1 to 15 do X[55+i]:=X3[i]; end; { продолжение программы }
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

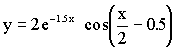
 x
x 
 + 1 = 25.
+ 1 = 25. z2 p = p3.
z2 p = p3. > ks, а во второй – остальные. Задача заключается в просмотре всех элементов исходного массива rsb и проверке каждого из них на условие rsbi > ks. Каждому элементу rsb, который удовлетворяет этому условию, присваивается очередной порядковый номер j и он переименовывается в элемент массива rse под этим номером. Каждому элементу, который этому условию не удовлетворяет, присваивается очередной номер k и он переименовывается в соответствующий элемент массива rso. Некоторую особенность в этой и аналогичных задачах представляет описание массивов. Объем исходного массива rsb в данном случае известен (n–элементов) а формируемых массивов rse и rso – нет, поэтому в описании всех трех массивов необходимо предусмотреть одинаковое максимально возможное число элементов n, которое обеспечивает нормальную работу программы в любом крайнем случае как в том, когда в элитную группу войдут все студенты, так и в том, когда в ней не окажется ни одного. Фрагмент программы, реализующий поставленную задачу (для конкретных условий n=150 и ks=4800), в котором ввод исходного массива rsb обозначен лишь условно может иметь вид:
> ks, а во второй – остальные. Задача заключается в просмотре всех элементов исходного массива rsb и проверке каждого из них на условие rsbi > ks. Каждому элементу rsb, который удовлетворяет этому условию, присваивается очередной порядковый номер j и он переименовывается в элемент массива rse под этим номером. Каждому элементу, который этому условию не удовлетворяет, присваивается очередной номер k и он переименовывается в соответствующий элемент массива rso. Некоторую особенность в этой и аналогичных задачах представляет описание массивов. Объем исходного массива rsb в данном случае известен (n–элементов) а формируемых массивов rse и rso – нет, поэтому в описании всех трех массивов необходимо предусмотреть одинаковое максимально возможное число элементов n, которое обеспечивает нормальную работу программы в любом крайнем случае как в том, когда в элитную группу войдут все студенты, так и в том, когда в ней не окажется ни одного. Фрагмент программы, реализующий поставленную задачу (для конкретных условий n=150 и ks=4800), в котором ввод исходного массива rsb обозначен лишь условно может иметь вид:


