
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Создание пробных, отладочных массивовСодержание книги
Поиск на нашем сайте
Массивы Цель данного пособия – краткое описание с рассмотрением соответствующих примеров основных вопросов программирования встречающихся при машинной обработке массивов числовых данных. При этом используется версия TURBO PASCAL 7.0 алгоритмического языка PASCAL. Для самостоятельной работы с пособием необходимо знать основные элементы этого языка: типы величин, операторы присваивания, перехода и циклических вычислений, а также способы ввода и вывода числовых и символьных данных. Для полного и успешного усвоения излагаемого материала целесообразна проработка приведенных в пособии примеров непосредственно на ЭВМ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. РАЗМЕРНОСТЬ И ОПИСАНИЕ МАССИВОВ, ИНДЕКСИРОВАНИЕ ИХ ЭЛЕМЕНТОВ Упорядоченная совокупность каких–либо однородных данных называется массивом. Примерами таких данных могут быть результаты экспериментов, цифры статистической отчетности, табличные значения той или иной функции, список фамилий сотрудников учреждения, их должностных окладов и т.п. Элементы каждого массива пронумерованы, хранятся в памяти ЭВМ под соответствующими номерами (индексами) и могут быть в любой момент вызваны по одному в программу для необходимых действий над ними. Работа с массивами имеет наибольший удельный вес и особое значение в практическом применении ЭВМ. Массивы могут быть числовыми и символьными, а также одно– и многомерными. Одномерный массив можно представить в виде строки или столбца соответствующих элементов, значение каждого из которых определяется его порядковым номером (индексом). В практике программирования одномерный массив часто называется вектором. Двумерный массив –это таблица, состоящая из нескольких строк и столбцов. Такие массивы принято называть матрицами. Значение каждого элемента матрицы определяется номерами (индексами) строки и столбца, которым принадлежит этот элемент. Трехмерный массив – это стопка матриц одного размера. Значение каждого элемента такого массива определяется номерами (индексами) страницы в стопке, а также строки и столбца на этой странице. Необходимо иметь в виду, что в языке PASCAL индексы могут выражаться константами, переменными и арифметическими выражениями. Таким образом размерность массива выражается количеством индексов, которое необходимо указать для определения каждого элемента этого массива:
для одномерного массива один индекс, например: X5, Y2, Zk, T2n–1 и т.п.; для двумерного два индекса, например: a3,4, bi,j, r2i,k+1 и т.п.; для трехмерного три индекса, например: U3,4,8, P2k,j+1,3m и т.п. Аналогично определяются массивы и большей размерности, которая в языке PASCAL практически не ограничена. Все элементы массивов в программах используются со своими индексами, которые записываются после имени массива в квадратных скобках и (если их несколько) разделяются запятыми: a[37]; v[k]; w[2*i+1]; x[3,5]; y[i,j]; z[k–1,2*m+1]; r[2,4,6]; s[k,l,m]; t[i+2,j–1,3*k+n]. При программировании работы с массивами прежде всего необходимо помнить, что каждый из них в программе должен быть описан. Это требование обязательно как для массивов, которые вводятся в качестве исходных данных, так и для тех, которые формируются в самой программе в результате каких–либо вычислений. Цель описания массива состоит в том, чтобы предупредить вычислительную систему об ожидаемом количестве элементов массива, под которые система резервирует необходимое число ячеек оперативной памяти, а также о порядке расположения элементов массива в этих ячейках, числе и типе индексов каждого элемента. Описание может осуществляться двумя способами: как в разделе типов (Type), так и в разделе переменных (Var). Например, массив Х, состоящий из 20 вещественных чисел с индексами от 1 до 20; может быть описан так: 1–й способ: Type X= array [1..20] of real; Var X: real; или 2–й способ: Var X: array [1..20] of real; Общий вид описания в разделе var: A: array [T1,Т2,...,Tк] of тип; где А– имя массива; Т1,Т2,...,Тk – типы индексов; тип – это тип элементов массива. Служебные слова array..... of real можно перевести как “массив из вещественных чисел”. Аналогично определяются массивы из других чисел, символов и т.п. Например, массив фамилий студентов академгруппы из 25 человек может быть описан так: Var Fam: array [1..25] of string[20]; В этом описании запись string[20]; означает, что массив состоит из строковых данных, длинной не более 20 символов (букв) каждое. Рассмотрим еще один пример: пусть в программе необходимо работать с матрицей М из целых чисел:
В данном случае элементы массива имеют тип integer. Массив двумерный; первый индекс–номер строки изменяется в пределах от 1 до 3; второй индекс–номер столбца изменяется от 1 до 4. Описание этого массива выглядит так:
м: array [1..3,1..4] of integer; Задав конкретные значения индексов, можно выбрать определенный элемент этого массива. Например, оператор n:=m[2,3] присвоит величине n значение, стоящее на пересечении 2–й строки и 3–го столбца, т.е. число 42. Аналогично, оператор к:=m[1,1] + m[3,3]; выполнит сложение чисел 10+19. Отметим здесь, что описание массивов в разделе Type более экономно в случаях использования в программе нескольких одинаковых по размерности и составу массивов, в то время как описание в разделе Var удобнее, когда в программе используются массивы разной размерности и состава. Например, фрагмент программы: Type mas= array [1..100] of real; Var x,y,z: mas; Описывает три одномерных массива вещественных чисел с количеством элементов до 100 шт. в каждом с именами х, y, z. Описание же этих массивов в разделе Var потребуют три строки: Var x: array [1..100] of real; y: array [1..100] of real; z: array [1..100] of real; Наконец, необходимо иметь в виду, что в описаниях массивов диапазон изменения индексов может быть большим, чем тот, что реально будет использоваться в программе. Так каждый из описанных выше массивов х, y, z в программе может состоять из любого числа элементов от 1 до 100, но не один не может иметь более 100 элементов. Далее в данном пособии рассматриваются задачи, связанные с обработкой одно– и двумерных числовых массивов. ВВОД И ВЫВОД МАССИВОВ Отметим прежде всего, что действия с массивами, как правило, предполагают многократное повторение тех или иных операций, поэтому основными операторами в этих действиях являются операторы циклические. Эта особенность в полной мере относится и к операциям ввода и вывода. Ввод массивов Если число элементов массива невелико, скажем порядка 10–15, то ввод его может быть выполнен обычным способом с помощью оператора read, включенного в простой (для одномерного массива) или сложный (для многомерного) цикл. Заметим также что, если массив вводится в качестве исходных данных, то для проверки правильности ввода целесообразно предусматривать и вывод вводимых величин. Рассмотрим соответствующие примеры: Пример 1.2. Ввести массив целых чисел l (к=1,2,...10) с одновременным выводом их для проверки. program Vvod 1; Var l: array [1..10] of integer; k: integer; Begin writeln ('Массив исходных данных') for k:=1 to 10 do Begin read (l[k]); write (l[k]); end; (продолжение программы) Пример 2.2. Ввести матрицу R(3,4)
Обозначим i – номер строки матрицы, j – номер столбца. Тогда общий элемент матрицы обозначится ri,j. При вводе элементов матрицы с клавиатуры по строкам необходимо после прочтения последнего элемента строки переходить к новой строке. Для этого удобно использовать комбинацию операторов read и readln. program Vvod 2; Var r: array [1..3,1..4] of real; i,j: integer; Begin for i=1 to 3 do Begin for j=1 to 3 do read(r[i,j]); readln(r[i,4]); end; (продолжение программы) Совершенно так же может быть осуществлен ввод этой матрицы по столбцам. В этом случае операторы циклов по индексам i и j следует поменять местами, а числа при вводе набирать в последовательности их расположения по столбцам. Соответствующий фрагмент программы применительно к данному примеру будет иметь вид: Begin for j:=1 to 4 do Begin for i=1 to 2 do read(r(i,j)); readln(r(3,j)); end; (продолжение программы) Отметим, что ввод массивов с помощью операторов read имеет одно существенное неудобство. Как известно, первоначальный вариант программы практически никогда не бывает без ошибок, которые могут обнаруживаться как на стадии компиляции программы, так и на стадии ее выполнения. В последнем случае выявление и исправление ошибок связано с многократными пробными запусками программы. При каждом таком запуске элементы массива приходится набирать на клавиатуре заново. Это весьма неудобно даже для массивов из 10–15 элементов, не говоря уже о больших.
Более удобным в таком случае является ввод с использованием констант типа массив, который при работе программы осуществляется автоматически. Пример 2.3. Ввести одномерный массив Vec: 8.2 4.9 9.7 6.3 3.1, а также матрицу Маt
В данном случае ввод может быть выполнен в разделе описания констант: program Vvod 3; {константы типа массив} Const Vec: array [1...5] of real=(8.2,4.9,9.7,6.3,3.1); Mat: array [1..3,1..4] of integеr=((10,20,30,40), (50,60,70,80),(25,35,45,55)); i,j: integer; Begin (продолжение программы) В дальнейшем в программе обращения к элементам описанных массивов будут обычными: Vес[i], Mat[i,j] и т.п. Общее правило использования констант типа массив таково: после описания массива и знака = числовые значения его элементов записываются в скобках через запятую, для двумерных массивов элементы каждой строки записываются в отдельных скобках. Однако и описанный способ ввода не слишком удобен, когда число элементов массива выражается десятками, не говоря уже о сотнях и более. В таком случае выходом из положения является предварительная запись массива в файл, хранящийся в памяти отдельно от программы. При каждом запуске программы чтение элементов массива из этого файла и передача их в программу будет осуществляться уже автоматически. Не излагая всех вопросов, относящихся к понятию файлов и к операциям с ними, проиллюстрируем этот способ на примерах записи файлов на диск. Эти примеры всегда могут быть использованы в качестве образцов, где следует оставить неизменным все стандартные части, изменив лишь имена и параметры в соответствии с конкретными условиями решаемой задачи. При записи массива в виде файла следует различать имя массива, програмное имя файла, а также его имя, под которым он записывается в соответствующий каталог на диск. Последние два имени могут быть как разными, так и одинаковыми. Пример 2.4. Записать в текущий каталог, в файл с именем fd (файл данных) массив y состоящий из 50 вещественных чисел: program Vvod4; Var fd: file of real; y: array [1..50] of real; k: integer; Begin assign(fd,'fd'); rewrite(fd); for k:=1 to 50 do writeln(fd,y[k]);
close(fd); End. По этой программе при наборе на клавиатуре каждого очередного числа y оно будет записываться под соответствующим номером в файл с именем fd. В этом фрагменте переменными(зависящими от выбора программиста) являются: имя файла – fd, имя массива – y; число элементов в нем –50, обозначение индекса – к, и место нахождения формируемого файла – запись 'fd' в операторе аssign. Все остальные записи являются стандартными. Поясним кратко смысл основных из них. Запись fd: file оf real; объявляет переменную fd файлом, состоящим из вещественных чисел. Оператор assign связывает файл, программное имя которого fd,с местом его расположение и именем, под которым он записывается на этом месте. В приведенном примере assign(fd,'fd') означает, что файл с именем fd записывается под тем же именем в текущий каталог. Оператор assign в данном случае мог бы выглядеть и так, например: assign (fd,'masdat') Это означало бы, что имя файла в программе fd, а его имя в текущем каталоге masdat. Если же, мы хотим записать этот файл в корневой каталог диска а: под именем, скажем, fajl.dat, то оператор assign следует представить в виде: assign (fd,'a:\fajl.dat') Иными словами в апострофах оператора assign записывается путь к месту нахождения формируемого файла и его имя на этом месте. Оператор rewrite (fd); открывает файл для записи, оператор close (fd) закрывает его. При необходимости вызова в программу массива, записанного в виде файла, выполняется аналогичная по смыслу группа операторов. Пример 2.5. Ввести массив а из 150 целых чисел, записанный файлом в каталоге DANNYE на диске A:, под именем mas.dat. program Vvod_5; Var f: file of integer; a: array [1..150] of integer; n: integer; Begin assign (f,'a:\DANNYE\mas.dat'); reset(f); for n:=1 to 150 do read (f,a[n]); close(f); (Продолжение программы) Здесь f – программное имя файла (разумеется произвольное); оператор Reset(f) открывает этот файл для чтения, все остальные операторы рассмотрены выше. По этому фрагменту 150 целых чисел, записанных на дискете, будут переданы в программу под именами а1,а2,...,а150 и могут обрабатываться в ней в соответствии с необходимостью. Begin for j:=1 to 6 do m[i,j]=round(10*sin(i+j)); end; Наиболее простым и удобным способом создания пробных массивов является использование специальной функции Random – датчика случайных чисел. Эта функция записывается в виде: Random или Random(N), где аргумент N представляет собой число или выражение целого типа. Если этот аргумент задан, функция генерирует случайные целые числа в интервале от 0 до N, если не задан, то вещественные числа в интервале 0–1. Например, включенный в цикл оператор Random (10), генерирует случайные целые числа в интервале от 0 до 10, а оператор Random–вещественные числа в интервале от 0 до 1. Если необходим вещественный массив, то целые числа, выдаваемые функцией Random, переводится в вещественные умножением (или делением) на любой вещественный множитель, а если необходимы положительные и отрицательные элементы массива, то они получаются вычитанием из результатов функции Random соответствующим образом подобранной константы. Рассмотрим, например оператор: a[i]:=Random(100)*0.521–26.0; Функция Random (100) при каждом i генерирует случайные целые числа в пределах от 0 до 100; множитель 0.521 преобразует эти числа в вещественные в пределах от 0 до 52.1. Т.к. примерно половина этих чисел будет меньше 52.1/2, то вычитаемое 26.0 преобразует их в отрицательные. В результате весь этот оператор при изменении индекса i от 1 до n, сформирует n случайных вещественных чисел в пределах –26 до +26.0. Примерно половина этих чисел будет положительными, остальные отрицательные.
Пример 2.7. Пусть необходимо создать пробный одномерный массив a из 20 целых чисел в пределах от 0 до 100, а также матрицу b размером 10x10 с вещественными элементами в пределах от –100 до 100. Поставленная задача может быть решена с помощью следующего программного фрагмента: program Massiv; Var a: array [1..20] of integer; b: array [1..10,1..10] of real; i,j,k: integer; Begin for k:=1 to 20 do a[k]:=Random(100); for i:=1 to 10 do Begin for j:=1 to 10 do b[i,j]=199.9*Random–100 end; (продолжение программы) В данном примере функция Random(100) генерирует случайные целые числа в пределах от 0 до 1, а функция Random–вещественные числа от 0 до 1. Множитель 199.9 преобразует их в вещественные в пределах от 0 до 199.9, а константа–100 переводит те из них, которые >100, в положительные числа, а те, которые <100, в отрицательные. Вывод одномерных массивов Так как элементы числового массива представляют собой числа одного происхождения и, как правило, одного порядка, то выводить их целесообразно во–первых в формате, а во–вторых в формате, едином для всего массива. Если число элементов массива невелико и все они уместятся в 1–3 строках на экране или принтере, то вывод таких массивов не требует каких либо особенностей. Например, вывод массива X из 8 элементов в формате 6:3 выполняется одним оператором: for k:=1 to 8 do write(x[k]:6:3); Массивы с большим числом элементов целесообразно выводить в форме таблиц с одинаковым количеством чисел в строках, используя сочетания операторов write и writeln. Напомним, что при записи оператора вывода в виде, например, write(a), следующая выводимая информация будет выводиться в той же строке, что и число а, при записи же в виде writeln(a), после вывода числа а следующая информация будет выводится с новой строки. Пример 2.8. Пусть массив Xк из 40 вещественных чисел требуется вывести в виде таблицы по 8 чисел в строке, т.е. разместить выводимые числа по следующей схеме: Х1 Х2 Х3.....Х8 Х9 Х10 Х11...Х16 .............................. Хi Хi+1 Хi+2...Хi+7 ............................... Х32 Х33 Х34....Х40 Из этой схемы видно, что если обозначить индекс первого числа в каждой строке через i, то этот индекс изменяется от 1 до 32 с шагом 8. В каждой строке индекс первого элемента может быть выражен как i+0, второго i+1, третьего i+2,... восьмого i+7, т.е. этот индекс имеет общую формулу i+j, где j изменяется от 0 до 7 с шагом 1. Отсюда фрагмент программы, реализующей вывод массива по данной схеме в формате, например 6:2, выразится двойным циклом по i и j и может быть представлен в виде: i:=1 while (i<=32) do Begin for j:=0 to 7 do write (x[i,j]:6:2); writeln; i:=i+8; end; В данном случае в каждой очередной строке выводится по 8 чисел, после чего оператор пустой writeln, прерывает строку и обеспечивает вывод очередной восьмерки с новой строки. При любом другом количестве элементов массива и количества чисел в строке нетрудно написать соответствующий фрагмент программы, если предварительно набросать схему вывода, аналогичную выше приведенной. Отметим еще следующее. Если количество элементов массива не кратно количеству чисел в строке, то всегда останется неполной последняя строка. Вывод этой строки можно выполнить отдельным оператором. Так, если бы в данном случае число элементов массива составляло не 40, а, например, 45, то для вывода последних 5 элементов к приведенному фрагменту программы следовало бы дописать оператор for j:=41 to 45 do write (x[j]:6:2); Вывод матриц Вывод двумерных массивов как и ввод требует использования двойных циклов, в одном из которых параметром является номер строки, а во втором – номер столбца. При этом матрицы, очевидно, целесообразно выводить в их естественном виде, т.е. в виде таблиц. Пример 2.9. Составить программу вывода матрицы А из целочисленных элементов размером m*n, т.е. имеющей m строк и n–столбцов. Пусть i–номер строки, j–номер столбца, тогда общий элемент матрицы обозначится аi,j и схема индексирования ее элементов будет иметь вид:
Вывод этой матрицы m строками по n чисел в строке в заданном формате, например:4, с заголовком может быть выполнен следующем образом: writeln (' Матрица A'); for i:=1 to m do Begin writeln; for j:=1 to n do write (a[i,j]:4); end; В этом фрагменте оператор пустой writeln отделяет заголовок от первой строки матрицы, он же обеспечивает переход к следующей строке после завершения вывода предыдущей. Begin for i:=1 to 25 do Begin x[i] = 0 + 0.25*(i–1); y[i] = 2*exp(1.5*x[i])*cos(x[i]/2–0.5); writeln('x=';x[i]:5:2;' y=';y[i]:6:3) end; end. Begin S:= S + x[k]; P:= P * x[k]; end; При суммировании и перемножении элементов двумерных массивов – матриц требуется перебирать все элементы по рядам: либо по строкам и в каждой строке по столбцам, либо по столбцам и в каждом столбце по строкам. Например вычислить сумму и произведение всех элементов матрицы A размером m * n (см. пример 2.9) можно с помощью следующих операторов: S:=0; P:=1; for i:=1 to m do Begin for j:=1 to n do Begin S:= S + a[i,j]; P:= P * a[i,j]; end; end; Результат не изменится, если в данном фрагменте операторы циклов по i и j поменять местами. Рассмотрим еще одну задачу, довольно часто встречающуюся в работе с массивами. Пусть дано два одинаковых по размеру массива X и Y (i=1,2,...n). Требуется вычислить величину SP = x1 y1 + x2 y2 +... + xi yi +... + xn yn. Отметим, что такая сумма – сумма попарных произведений одноименных элементов двух массивов (векторов) называется скалярным произведением этих массивов. Вычисление этого произведения может быть выполнено так: SP:= 0; for i:=1 to n do SP:= SP + x[i]*y[i]; Задачи выборок Задачи выборок могут ставиться по разному, но в общем случае сводятся к выбору из данного массива элементов с заданными свойствами или по заданному признаку. Пример 5.1. Дан массив mz месячных заработков сотрудников предприятия (i=1,2,...n). Пусть p – процентная ставка подоходного налога, который вычитается из суммы заработка: при mz < z1 p = p1; при z1 при mz Рассчитать сумму подоходного налога sn и сумму причитающейся получки sp каждого сотрудника. Задача, очевидно, сводится к просмотру всего массива заработков и выбору из него сумм, попадающих в пределы: < z1; от z1 до z2; > z2, после чего суммы налогов и получки вычисляются по формулам sn = mz * p/100 и sp = mz – sn. где p принимает значения p1, p2, p3 в зависимости от величины mz. Соответствующий фрагмент программы в предположении, что массив mz и константы n, z1, z2, z3, p1, p2, p3 введены, может иметь вид for i:=1 to n do Begin if mz[i]<z1 then p:=p1; if mz[i]>=z1 and mz[i]<z2 then p:=p2; if mz[i]>=z2 then p:=p3; sn:= mz[i]*p div 100; sp:=mz[i] – sn; write(i:2,' Заработок ',mz[i]:6,' Налог ',sn:6,' Получка ',sp:6); end; Аналогично выполняется и выборка элементов двумерных массивов. Пример 5.2. В двумерном массиве p размером 6? 8 выбрать все отрицательные числа, вывести их и подсчитать их общее количество. Если искомое количество отрицательных элементов обозначить k, то соответствующий фрагмент программы может иметь вид: k:=0; for i:=1 to 6 do Begin for j:=1 to 8 do Begin if p[i,j]<0 then Begin k:=k+1; write(p[i,j]); end; end; end; write(' Число отрицательных элементов k=',k); 5.2 Преобразование одних массивов в другие Задачи этого типа тесно связаны с задачами выборок и суть их легко понять из рассмотрения соответствующих примеров. Пример 5.3. Пусть rsbi – рейтинговая сумма балов i–го студента за 1–й этап обучения (i=1..n). Студенты, набравшие сумму балов, не менее некоторой контрольной ks, образуют элитную группу и могут быть переведены на 2–й этап обучения. Допустим требуется проанализировать средние показатели успеваемости элитной и остальной групп по отдельности. Это означает, что общий массив rsb необходимо разделить на 2 массива rse и rso, отобрав в первый из них суммы балов program Rejting; Const n=150; ks=4800; Type mas= array [1..n] of integer; Var rsb,rse,rso:mas;i,j,k:integer; Begin { ввод массива rsb } j:=0; k:=0; for i:=1 to n do Begin if rsb[i]>=ks then Begin j:=j+1; rse[j]:=rsb[i]; End Else Begin k:=k+1; rso[k]:=rsb[i]; end; end; writeln(' Элитный массив '); for i:=1 to j do write(rse[i]:8); writeln; writeln(' Остальной массив'); for i:=1 to k do write(rso[i]:8); end. Рассмотрим аналогичный пример с двумерным массивом. Пример 5.4. В матрице А(10х10) выбрать числа больше 8 и меньше 2 и сформировать из них два одномерных массива – вектора B и C. Ниже приводится фрагмент программы в котором исходная пробная матрица формируется с помощью функции Random (см. раздел 2.2).Единственное, что требует пояснения в данном случае. это заказ количества элементов в описании формируемых массивов B и C. Оно, очевидно, должно указываться как и в предыдущем примере с "запасом", на случай, если все элементы матрицы попадут в один или другой массив B или C, т.е. должно быть равно 100. program MatrVec; Type vec= array [1..100] of real; Var a: array [1..10,1..10] of real; b,c:vec; i,j,k,l:integer; Begin writeln(' Исходная матрица '); for i:=1 to 10 do Begin for j:=1 to 10 do Begin a[i,j]:=9.999*Random; write(a[i,j]:5:2); end; writeln; end; k:=0; i:=0; for i:=1 to 10 do Begin for j:=1 to 10 do Begin if a[i,j]>8 then Begin k:=k+1; b[k]:=a[i,j]; End else if a[i,j]<2 then Begin l:=l+1; c[l]:=a[i,j]; end; end; end; writeln(' Вектор B '); for i:=1 to k do write(b[i]:5:2); writeln(' Вектор C'); for i:=1 to l do write(c[i]:5:2); end. К задачам преобразования массивов относятся и задачи слияния нескольких однородных массивов в один. Пример 5.5. Пусть, например, в эксперименте выполнено 3 серии измерений некоторой величины X. При этом в первой серии выполнено 25 измерений, во второй 30 и в третьей 15. Иными словами, получено 3 массива данных: X1 (i=1..25); X2 (i=1..30) и X3 (i=1..15). Требуется объединить три массива в один общий массив X, расположив в нем сначала элементы массива X1, затем X2, затем X3 и обеспечив общую сквозную нумерацию элементов массива X (i=1..70). В этом случае, очевидно, 25 первых элементов массива X совпадут с одноименными элементами массива X1, то есть перенумеровка элементов массива X1 в элементы массива X будет выполняться по формуле Xi = X1i (i=1..25). Затем первый элемент массива X2 должен стать 26–м элементом массива X и т.д. То есть каждый i–й элемент массива X2 должен переименоваться в 25+i –й элемент массива X. Иными словами, перенумеровка элементов массива X2 в элементы массива X должна выполняться по формуле X25+i= X2i (i=1..30). В конце этого цикла очевидно получим X55 = X230. Далее, первый элемент массива X3 должен стать 56–м элементом массива X и, рассуждая аналогично предыдущему, получим, что перенумеровка элементов массива X3 в элементы массива X должна выполняться по формуле X55+i = X3i (i=1..15). Соответствующий фрагмент программы слияния массивов, реализующий данный алгоритм представлен ниже. Отметим, что в данном случае описания всех четырех массивов целесообразно выполнить в разделе Type, заказав для каждого из них размер наибольшего, а именно массива X, включающего суммарное количество 70 элементов. program SliMas; Type vec= array [1..70] of real; Var X1,X2,X3,X:vec; i:integer; Begin Begin { ввод массивов X1,X2,X3 } end; Begin for i:=1 to 25 do X[i]:=X1[i]; for i:=1 to 30 do X[25+i]:=X2[i]; for i:=1 to 15 do X[55+i]:=X3[i]; end; { продолжение программы } Begin if t[i]<=min then Begin min:=t[i]; k:=i; end; end; writeln(min,k); { продолжение программы } Очевидно, если знак <= в операторе if заменить на >=, то получим фрагмент программы определяющей наибольший элемент массива. В этом случае, разумеется, логично заменить имя min на max. Если нас интересует лишь сама величина наименьшего или наибольшего элемента, а его место в массиве безразлично, то приведенный фрагмент упрощается удалением оператора k:=i. Возможно в одном цикле одновременно определять наименьший и наибольший элементы. Покажем это на примере двумерного массива. Пример 5.7. В матрице X(m? n) найти наименьший элемент min и наибольший max и определить индексы каждого из них. Если обозначить индексы наименьшего и наибольшего элементов матрицы соответственно k1,l1 и k2,l2, то задача может быть решена следующим фрагментом: k1:=1; l1:=1; k2:=1; l2:=1; min:=X[1,1]; max:=X[1,1]; for i:=1 to m do Begin for j:=1 to n do Begin if X[i,j]<min then Begin min:=X[i,j]; k1:=i; l1=j; End else if X[i,j]>max then Begin max:=X[i,j]; k2:=i; l2:=j; End end; end; writeln('min=',min,' i=',k1,' j=',l1); writeln('max=',max,' i=',k2,' j=',l2); Begin s1:=s1+x[i]; s2:=s2+s2+sqr(x[i]); end; xsr:=s1/n; dis:=(s2/n–sqr(xsr))*n/(n–1); sko:=sqrt(dis); writeln; write('xsr=',xsr,' dis=',dis,' sko=',sko); Кроме среднего арифметического иногда используются еще три вида средних величин, вычисляемых по формулам: среднее квадратическое (оно не равно среднеквадратическому отклонению)
среднее геометрическое
среднее гармоническое
Вычисление этих величин сводится в конечном итоге к вычислению соответствующих сумм и произведения и не представляет труда. Begin writeln('Исходная матрица'); for i:=1 to 10 do Begin for j:=1 to 8 do Begin a[i,j]:=19.9*Random; write(a[i,j]:6:2); end; writeln; end; writeln('Строчные суммы'); i:=2; while (i<=10) do Begin s[i]:=0; for j:=1 to 8 do s[i]:=s[i]+a[i,j]; write(s[i]:10:3); i:=i+2; end; writeln('Столбцовые произведения'); j:=1; while (j<=7) do Begin p[j]:=1; for i:=1 to 10 do p[j]:=p[j]*a[i,j]; writeln(p[j]:15:3); j:=j+2; end; end. Пример 6.2. В некоторых задачах математики приходится вычислять сумму элементов квадратной матрицы, стоящих на ее главной диагонали. Главной называется диагональ, идущая из левого верхнего в правый нижний угол. Такая сумма носит название следа матрицы. Пусть заданная матрица А является квадратной с размером 8? 8. Тогда если обозначить искомую сумму Sled и обратить внимание на то, что у элементов главной диагонали оба индекса одинаковы, т.е. i=j, задача вычисления указанной суммы решится двумя строками: writeln('След матрицы'); sled:=0; for i:=1 to 8 do Sled:=Sled+a[i,i]; writeln('Sled=',Sled); Пример 6.3. В матрице А произвольного размера m? n найти и вывести (строкой) строку с наибольшим произведением, а также (вывести столбцом) столбец с наименьшей суммой всех своих элементов. Обозначим строковые произведения pi (i=1..m), наибольшее из них Pmax, а его порядковый номер k. Аналогично: столбцовые суммы sj (j=1..n), наименьшая из них Smin, а ее индекс l. Задача, очевидно, сводится к вычислению элементов массивов p и s, нахождению в первом из них наибольшего элемента, а во втором наименьшего с одновременными определениями их индексов k и l, после чего k–я строка должна быть выведена в строку, а l–й столбец столбцом. Эта задача в предположении, что массивы A, P, S надлежащим образом описаны и первый из них введен, а два других сформированы (как это делается, см. пример 6.1), может быть реализована следующим фрагментом (при m=8, n=10): k:=1; Pmax:=p[k]; for i:=1 to 8 do Begin if p[i]>=Pmax then Begin Pmax:=p[i]; k:=i; end; end; writeln('Строка с Pmax'); for j:=1 to 10 do write(a[k,j]); writeln; l:=1; Smin:=s[l]; writeln('Столбец с Smin'); for j:=1 to 10 do Begin if s[j]<=Smin then Begin Smin:=s[j]; l:=j; end; end; for i:=1 to 8 do writeln(a[i,l]); Пример 6.4. Дана матрица А(m? n). Составить вектор B из наибольших элементов каждой строки и вектор С из наименьших элементов каждого столбца. Алгоритм решения данной задачи состоит, очевидно, в том, чтобы в каждой i–й строке (i=1..m) найти ее наибольший элемент и присвоить его значение элементу bi вектора B. Аналогично, в каждом j–м столбце (j=1..n) требуется найти его наименьший элемент и присвоить его значение элементу cj вектора С. Соответствующий фрагмент программы (при m=8, n=10) с выводом полученных векторов: for i:=1 to 8 do Begin max:=a[i,1]; for j:=1 to 10 do Begin if a[i,j]>max then max:=a[i,j]; end; b[i]:=max; end; for j:=1 to 10 do Begin min:=a[1,j]; for i:=1 to 8 do Begin if a[i,j]<min then min:=a[i,j]; end; c[j]:=min; end; writeln('Вектор В'); for i:=1 to 8 do write(b[i]:6:2); writeln; writeln('Вектор C'); for j:=1 to 10 do write(c[j]:6:2); Задачи, аналогичные рассмотренным выше, в разных комбинациях могут встречаться и в других более сложных случаях работы с матрицами. В таких ситуациях соответствующие программы с точностью до обозначений могут комбинироваться из фрагментов разобранных в данном разделе. КОНТРОЛЬНЫЕ ВОПРОСЫ И УПРАЖНЕНИЯ 1. Дайте определение массива. Приведите примеры. 2. Что такое одн
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.168.40 (0.016 с.) |


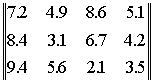


 mz < z2 p = p2;
mz < z2 p = p2; z2 p = p3.
z2 p = p3. > ks, а во второй – остальные. Задача заключается в просмотре всех элементов исходного массива rsb и проверке каждого из них на условие rsbi > ks. Каждому элементу rsb, который удовлетворяет этому условию, присваивается очередной порядковый номер j и он переименовывается в элемент массива rse под этим номером. Каждому элементу, который этому условию не удовлетворяет, присваивается очередной номер k и он переименовывается в соответствующий элемент массива rso. Некоторую особенность в этой и аналогичных задачах представляет описание массивов. Объем исходного массива rsb в данном случае известен (n–элементов) а формируемых массивов rse и rso – нет, поэтому в описании всех трех массивов необходимо предусмотреть одинаковое максимально возможное число элементов n, которое обеспечивает нормальную работу программы в любом крайнем случае как в том, когда в элитную группу войдут все студенты, так и в том, когда в ней не окажется ни одного. Фрагмент программы, реализующий поставленную задачу (для конкретных условий n=150 и ks=4800), в котором ввод исходного массива rsb обозначен лишь условно может иметь вид:
> ks, а во второй – остальные. Задача заключается в просмотре всех элементов исходного массива rsb и проверке каждого из них на условие rsbi > ks. Каждому элементу rsb, который удовлетворяет этому условию, присваивается очередной порядковый номер j и он переименовывается в элемент массива rse под этим номером. Каждому элементу, который этому условию не удовлетворяет, присваивается очередной номер k и он переименовывается в соответствующий элемент массива rso. Некоторую особенность в этой и аналогичных задачах представляет описание массивов. Объем исходного массива rsb в данном случае известен (n–элементов) а формируемых массивов rse и rso – нет, поэтому в описании всех трех массивов необходимо предусмотреть одинаковое максимально возможное число элементов n, которое обеспечивает нормальную работу программы в любом крайнем случае как в том, когда в элитную группу войдут все студенты, так и в том, когда в ней не окажется ни одного. Фрагмент программы, реализующий поставленную задачу (для конкретных условий n=150 и ks=4800), в котором ввод исходного массива rsb обозначен лишь условно может иметь вид: ;
; ;
; .
.


