
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Лагранжа,теорема КошиСодержание книги Поиск на нашем сайте
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция непрерывна на отрезке[a,b] и дифференцируема в интервале(a,b), то найдётся такая точка c э (a,b), что Доказательство Для функции одной переменной:
Введем функцию
что и требовалось доказать. Теорема Коши 1)Пусть f(x),g(x) определены на [a,b] 2)сущ-ют производные f’(x),g’(x) на интервале(a,b) 3)g’(x) не равно 0,любое Х э [a,b],тогда Существует С, a<c<b, f’(c)/g’(c)=f(b)-f(a)/g(b)-g(a) Док-во g(b) не равно g(a) составим вспомогательную фун-ию F(x)=f(x)-f(a)-f(b)-f(a)/g(b)-g(a)*(g(x)+g(a)) непрерывна F’(x)=f’(x)- f(b)-f(a)/g(b)-g(a)*g’(x) F(a)=f(a)-f(a)-(f(b)-f(a)/g(b)-g(a))*(g(a)-g(a))=0 F(b)=f(b)-f(a)-(f(b)-f(a)/g(b)-g(a))*(g(b)-g(a))=0 Сущ-ет С F’(c)=0 отсюда следует f’(c)-(f(b)-f(a)/g(b)/g(a))*g’(c)=0 F’(c) /g’(c)=f(b)-f(a)/g(b)-g(a) Дифференциалы высших порядков. Формула Лейбница Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференци-ал этой функции. Дифференциал от дифференциала есть второй дифференциал. Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответ-ствующей степени дифференциала независимой пере-менной. Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее диф-ференциала соответствующего порядка к соответству-ющей степени дифференциала независимой перемен-ной.
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
Если функция дифференцируема в, то производная первого порядка определяется соотношением
Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда
Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
Формула Лейбница Y^(n)=(U*V)^n=Сумма (от n до k=0) U^(n-k)*V^(k) Вторая производная для функции, заданной параметрически (f’(x))’-производная второго порядка F’’(x); Y’’=d^2y/dx^2 29. Правило Лопиталя: Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида и. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных. Условия 1. 2.f(x)и g(x) дифференцируемы в проколотой окрестности 3. 4. существует Пределы также могут быть односторонними. Теорема. Пусть f(x),g(x) непрерывны и дифференцируемы в окрестности т.а и равны нулю в этой точке. Пусть g’(a)не равно нулю,тогда если сущ-ет limf’(x)/g’(x)=l,то lim f(x)/g(x)= lim f’(x)/g’(x)=l Замечание 1. Теорема верна в том случае,если ф-и f(x) и g(x) не определены в точке а,но сущ-ет limf(x)=0,lim g(x)=0 Замечание 2. Т.верна в том случае,если х принадлежит Замечание 3 Если lim f’(x)/g’(x)=0/0 дифференцирование можно повторить еще раз Экстремумы функции. Необходимое и достаточное условие экстремума. Z=f(x,y) (x,y)э Д (Xo,Yo)наз-ся точкой максимума, если сущ-ет дельта-окрестность Xo-Q<X<Xo+Q Yo-Q<Y<Yo+Q, в которой f(x,y)<f(Xo,Yo) Точка минимума f(x,y)>(Xo,Yo) Необходимое условие экстремума Y=f(x)=df/dx=0 Z=f(x,y)= df/dx=0 и df/dy=0 Точки, удовлетворяющие этой системе-критические точки Достаточное условие экстремума Пусть(Xo,Yo)-критические точки А11=d^2f/dx^2 A12=d^2/dxdy A22=d^2/dy^2 Дельта>0(Xo,Yo)-экстремум (А11<0-макс) (А11>0-минимум) Дельта<0-экстремум нет Дельта =0 – нет ни мин ни макс
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.3.204 (0.009 с.) |

 Геометрически это можно переформулировать так: на отрезке[a,b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Геометрически это можно переформулировать так: на отрезке[a,b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка. . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка, в которой производная функции F равна нулю:
. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка, в которой производная функции F равна нулю:




 или
или 
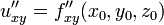 или
или 
 или
или 

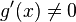 в проколотой окрестности
в проколотой окрестности 





