
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически определимые фермыСодержание книги Поиск на нашем сайте
2.1 Классификация ферм Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирными. При этом нагрузка к ферме прилагается в узлах, а в стержнях возникают только продольные усилия N. Ферма, как правило, состоит из нескольких однотипных элементов ¾ панелей, при этом стержни фермы имеют свои названия (рис. 2.1):
Фермы классифицируются по следующим признакам:
1.1. По типу решетки:
1.2. По очертанию:
1.3. По типу опирания: балочные, консольные, консольно-балочные; 1.4. По назначению: стропильные, башенные, крановые, мостовые с ездой понизу и поверху, и др.
Расчет простейших ферм на неподвижную нагрузку Фермы, образованные из шарнирных треугольников последовательным присоединением узлов, называются простейшими. Они статически определимы и геометрически неизменяемы. В задачах расчета статически определимых ферм в полной мере приходится использовать уравнения равновесия как сходящейся системы сил (при рассмотрении равновесия узла), так и произвольной системы сил. Необходимо отметить, что все методы определения усилий в стержнях фермы реализуют основной метод механики деформируемого твердого тела - метод сечений. Принято различать три основных способа определения усилий в стержнях ферм: 1) метод моментной точки используется, когда в поперечном сечении оказывается не более трех неизвестных усилий в стержнях; при этом два из них пересекаются в точке, положение которой легко определить. В сумму моментов всех сил, приложенных к рассматриваемой части фермы относительно этой точки, которая называется моментной, войдет только одно неизвестное, которое из этого уравнения и будет найдено; 2) метод проекций. В этом случае записывают сумму проекций всех сил, приложенных к рассматриваемой части фермы на ось х или у или другую произвольно ориентированную ось. Ось проекции выбирается так, чтобы в уравнение равновесия входило одно неизвестное усилие; 3) метод вырезания узлов применяется для определения усилий, когда в узле сходится не более двух стержней с неизвестными усилиями.
Пример 2. 1. Определить нулевые стержни заданной консольной фермы (рис. 2.2). Вырежем узел 9 и рассмотрим его равновесие (рис. 2.3). Узел не нагружен, и в нем сходятся два стержня. Из уравнения равновесия S y = 0 получим: N 97sina = 0, откуда N 97 = 0. Запишем второе уравнение равновесия: S x = 0, - N 97cosa - N 98 = 0, тогда N 98 = 0. Таким образом, оба усилия, сходящиеся в двухстержневом ненагруженном узле, нулевые.
Рассмотрим равновесие 8-го узла (рис. 2.4). Это так называемый трехстержневой узел с единственно выходящим стержнем. Им является стержень 8–7. Записав сумму проекций S y = 0, нетрудно убедиться, что стержень 8–7 — нулевой, а из уравнения S х = 0 следует, что N 98 = N 86. Мысленно вырежем узел 7. С учетом того, что стержень 7–8 нулевой, 7-й узел можно рассматривать как трехстержневой с единственно выходящим стержнем 7–6, который тоже будет нулевым. Остальные узлы либо нагружены, либо не могут рассматриваться как трехстержневые, и в остальных стержнях решетки будут возникать продольные усилия. Пример 2. 2 Вычислить усилия в отмеченных стержнях фермы (рис. 2.5). Наметим путь решения задачи. Усилие в стержне 3–4 удобно искать, рассмотрев равновесие узла 3; усилие в стержне 5–6 проще найти методом вырезания узла 6, а усилие в раскосе 4–5 удобнее находить, используя метод проекций. Для этого необходимо найти реакции опор и провести сечение I–I. S m 1 = 0. P∙ 6– R пр ∙ 12 = 0, R пр = R л = Р /2. Для определения усилия в стержне 3–5 можно воспользоваться методом моментной точки, которая находится в месте пересечения двух других усилий, оказавшихся в сечении I–I. Моментной точкой для N 35 служит узел 4 (рис. 2.5, б).
Дальнейшее решение задачи предлагается провести студентам самостоятельно. Вырезав узел 3, получим N 34 = 0; вырезав узел 6, нетрудно убедиться, что стойка 5–6 сжата усилием P (N 56 = - Р), а спроектировав все силы, приложенные к левой или правой частям фермы на вертикальную ось, получим усилие в раскосе N 54 = R л/cosa = 0,5 P /0,8 = = 0,625 P. Записав уравнение моментов для левой части фермы относительно узла 4, найдем N 35 = R л3/4 = 0,375 Р. Пример 2. 3. Определить усилия в стержнях третьей панели заданной фермы (рис. 2.6, а). При расчетах принять: d = 3,6 м, h = 3 м, h 1 = 0,4 h = 1,2 м и Р = 80 кН.
Итак, нам необходимо определить усилия в пяти стержнях фермы: в стержнях верхнего и нижнего пояса 5–7 и 4–6, в раскосе 4–7, в левой 4–5 и правой 6–7 стойках третьей панели. Предварительно вычислим ряд геометрических параметров заданной фермы, обозначив размер h - h 1 = h 2.
cosa = d / l 57 = 3,6/3,71 = 0,97, sina = (h 2/2)/ l 57 = 0,9/3,71 = 0,242; tga = 0,9/3,6 = 0,25; с = h 1/tga = 1,2/0,25 = 4,8 м; cosb = d / l 47 = 3,6/4,17 = 0,863; sinb = (h 1 + h 2/2)/ l 47 = 2,1/4,17 = 0,504.
1. Определяем опорные реакции. S mA = 0. - P∙d - P∙ 2 d - P∙ 3 d - P∙ 4 d + RВ∙ 4 d = 0; RВ = 200 кН. В силу симметрии RА = RВ = 200 кН.
2. Для определения усилий в стержнях 4-6, 4-7 и 5-7 разрежем третью панель сечением I-I и рассмотрим равновесие одной из частей фермы под действием внешних и внутренних сил (рис. 2.6, б). Рассматривая правую часть фермы, видим, что для определения N 46 удобно записать уравнение моментов относительно моментной точки 7 (узла 7), в которой пересекаются два других неизвестных усилия N 47 и N 57. S m 7=0. - P∙d + Rb∙d - N 46(h 1+ h 2/2) = 0. N 46 = (- 80×3,6 + 200×3,6)/2,1 = 206 кН. Усилие N 46 направлено на чертеже от узла и получилось положительным, следовательно, стержень 4-6 растянут. Для определения усилия N 57 также удобно использовать метод моментной точки (узел 4). Рассмотрим равновесие левой части фермы. S m 4 = 0. – Rа∙ 2 d + P∙ 2 d + P∙d - (N 57cosa) h = 0. N 57 = (- 200 ∙ 7,2 + 80 ∙ 7,2 + 80 ∙ 3,6)/(0,97×3) = - 198 кН.
Знак «-» у усилия N 57 говорит, что стержень 5-7 сжат. Усилие N 47 можно найти либо методом проекций на ось у всех сил, приложенных к одной из частей фермы, либо методом моментной точки. В данном случае это будет точка m, лежащая справа от опоры В (рис. 2.6). Воспользуемся методом проекций, рассмотрев равновесие левой части фермы (рис. 2.6, б). S y = 0. RА - P - P - P - N 57sina + N 47sinb = 0. N 47 = [- 200 + 80 + 80 + 80 + (- 198) ∙ 0,242]/0,504 = - 15,7 кН (стержень сжат).
Для вычисления усилия в стержне 6-7 проведем сечение II-II (рис. 3.32, а) и рассмотрим равновесие правой части фермы (рис. 2.7). Воспользуемся методом моментной точки: для усилия N 67 моментной точкой будет точка m, в которой пересекаются два других усилия N 46 и N 78. S mm = 0, - N 67(d + c) + Pc - Rbc = 0. N 67 = (80 ∙ 4,8 - 200 ∙ 4,8)/8,4 = - 69 кН, (стержень 6-7 сжат).
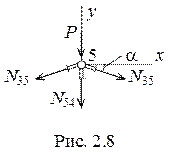
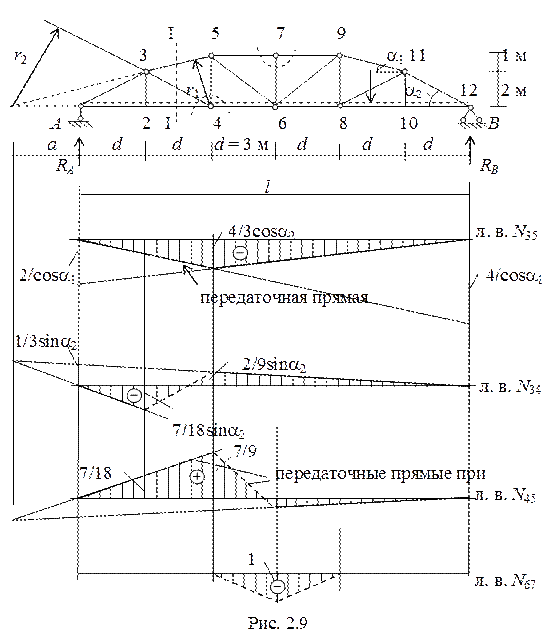
В стойке 5-6 усилие будем определять методом вырезания узлов, вырезав узел 5 (рис. 2.8). Спроецируем все усилия, сходящиеся в узле, на ось у. В силу симметрии фермы и внешней нагрузки усилие в стержне 3-5 примем равным усилию в стержне 5-7. S y = 0. - P - N 45 - N 57sina - N 35sina = 0; N 45 = - 80 -2(-198) ∙ 0,242 = 15,8 кН, cтойка 4 - 5 растянута. Для проверки полученных усилий можно записать уравнение проекций всех сил, приложенных к левой или правой частям фермы (рис. 2.6, б) на ось х. S x = 0. N 57cosa + N 47cosb + N 46 = 0; (- 198) ∙ 0,97 + (-15,7) ∙ 0,863 + 206 = - 205,6 + 206 = 0. Погрешность d, полученная в результате проверки, равна: d = (206 - 205,6) ∙ 100%/205,6 = 0,2%, при допустимой (разрешенной) для данного типа задач 3-5%. 2.3 Расчет ферм на подвижную нагрузку Расчет ферм на подвижную нагрузку сводится к построению линий влияния при действии на ферму подвижной единичной силы, перемещающейся по одному из поясов. Порядок построения линий влияния в фермах рассмотрим на примере. Рассмотрим построение линий влияния усилий N 35, N 34, N 45, и N 67 для фермы, показанной на рис. 2. 9.
Для построения линии влияния (а это график) усилия в стержне 3-5 необходимо получить выражение для этого усилия в зависимости от положения единичной силы. В свою очередь, единичная сила Р = 1 перемещается по нижнему поясу – это отмечено пунктирной линией. Для определения усилия N 35 разрежем вторую панель сечением I-I и воспользуемся методом моментной точки. Моментной точкой является узел 4. Пусть единичная сила перемещается справа от разрезанной панели между 4 и 12 узлами. Рассмотрим равновесие левой части фермы. S m 4= 0, RА ∙2 d + N 35∙ r 1= 0. (r 1 = h cosa1)
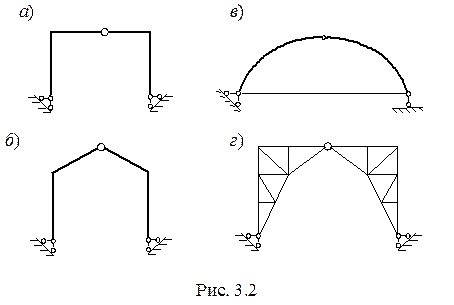
л. в. N 35 = Для построения правой ветви линии влияния N 35 отложим на левой опорной вертикали ординату 1∙2/cosa1. Поскольку линия влияния имеет знак минус, указанную ординату откладываем вниз. Правая ветвь будет проходить от 12 до 4 узла. Р =1 находится слева от разрезанной панели между 1 и 2 узлами. Рассмотрим равновесие правой части фермы. S m 4= 0, RВ ∙4 d + N 35∙ r 1= 0. По аналогии л. в. N 35 = Откладывая на правой опорной вертикали ординату 1∙4/cosa2, строим левую ветвь линии влияния N 35 от 1 до 2 узла. Движение единичной силы между 2 и 4 узлами можно осуществить по настилу. В этом случае будет иметь место узловая передача нагрузки, а линия влияния будет очерчена передаточной прямой (пунктирной линией), соединяющей левую и правую ветви. Отметим, что левая и правая ветви пересекаются под моментной точкой. Это свойство линий влияния можно использовать для проверки. Построим, используя приведенную выше методику, линию влияния усилия N 34. Моментная точка для этого усилия находится в точке «к», в точке пересечения продолжения стержней 2-4 и 3-5. Из подобия треугольников находим, что а = d = 3 м, плечо у усилия N 34 относительно моментной точки составит r 2 = 3 d∙ sina2. Р = 1 справа от разрезанной панели. S m к= 0, RА ∙ а - N 34∙ r 2= 0. л. в. N 34 = Строим правую ветвь, отложив на левой опорной вертикали 1/3sina2. Ординату под 4 узлом (2/9sina2) находим из подобия треугольников. Р = 1 слева от разрезанной панели. S m к= 0, RВ ∙7 d + N 34∙ r 2= 0. л. в. N 34 = Строим левую ветвь, отложив вниз на правой опорной вертикали 7/3sina2. В районе второго узла ордината составит 1/6 от 7/3sina2. Передаточной прямой соединяем левую и правую ветви. Не трудно убедиться, что они пересекаются под моментной точкой. Для определения усилия N 45 и построения его линии влияния можно так же воспользоваться методом моментной точки (точка «к») или методом вырезания узлов. Действительно, вырезав узел 4 (рис. 2.10) можно увидеть что в уравнение S у = 0 входит одно неизвестное N 45. Линия влияния усилия N 34 нами получена.
Рассмотрим равновесие 4 узла. S у = 0. N 34sina2 + N 45 = 0. N 45 = - N 34sina2, или л. в. N 45 = - (л. в. N 34)∙sina2 Вырезая узел 4, нам пришлось разрезать вторую и четвертую панели, т. е. левая ветвь линии влияния проходит от1 до 2 узла, а правая от 6 до 12 узла. Строим эти ветви. В качестве промежуточного будет положение единичной силы в 4 узле (рис. 2.11). В этом случае S у = 0. N 34sina2 + N 45 – Р = 0. N 45 = - N 34sina2 + 1 = - Откладываем в районе 4 узла 7/9 и проводим две передаточные прямые. Получили линию влияния N 45. Необходимо обратить внимание где пересекаются левая и правая ветви линии влияния N 45. При езде понизу усилие в стержне 6-7 равно нулю – стержень 6-7 нулевой. В то же время, при езде поверху при движении единичной силы между 5 и 9 узлами в стойке 6-7 будет возникать нагрузка. При движении по остальной части верхнего пояса стержень 6-7 остается нулевым, следовательно левая (от 1 до 5 узла) и правая (от 9 до 12 узла) ветви линии влияния усилия N 67 тоже нулевые. Воспользуемся методом вырезания узлов, когда сила Р = 1 находится в 7 узле (рис. 2. 12). S у = 0. – N 67 – Р = 0.. N 67 = – 1. Откладываем ординату (– 1) от проекции 7 узла, проводим передаточные прямые и получаем линию влияния N 67. 3. Трехшарнирные арки Арочными называются системы криволинейного или ломаного очертания, в опорах которых от вертикальной нагрузки возникают наклонные реакции, направленные, как правило, внутрь пролета. Горизонтальная составляющая такой наклонной реакции называется распором. Арочные системы в сравнении с балочными оказываются экономически более выгодными за счет меньших, чем в балках, изгибающих моментов.
Двухшарнирные и безшарнирные арки являются статически неопределимыми и будут рассматриваться в соответствующем разделе. Трехшарнирная арка является системой геометрически неизменяемой и статически определимой. Принятые обозначения в арках показаны на рис. 3.1. В практике встречаются различные по форме и виду арки. В том случае, когда каждая половина трехшарнирной арки представляет собой сплошной брус криволинейного очертания, ее называют аркой со сплошной стенкой (рис. 3.1). При ломаном очертании оси сооружение обычно называют трехшарнирной рамой (рис. 3.2, а, б). Система, изображенная на рис. 3.2, в, носит название трехшарнирной арки с затяжкой.
В практике встречаются арки, образованные из двух ферм, соединенных между собой общим шарниром (рис. 3.2, г). Такие системы называются трехшарнирными фермами. 3.1 Аналитический расчет трехшарнирной арки Определение опорных реакций
При действии внешней нагрузки на трехшарнирную арку (рис. 3.3) в каждой ее опоре возникает по две реакции. Всего, таким образом, имеется четыре неизвестные реакции – две вертикальные RA, RB и две горизонтальные НA и НB. Для расчета трехшарнирной арки кроме трех уравнений равновесия, которые дает статика для системы сил, расположенной в одной плоскости, можно составить четвертое уравнение, основанное на том, что сумма моментов всех сил, приложенных по одну сторону от ключевого шарнира С, равна нулю. Действительно, это уравнение для изгибающего момента в поперечном сечении, а в шарнире момент отсутствует. Для трехшарнирной арки (рис. 3.3) при определении реакций будут записаны следующие уравнения: S mB = 0, - RAl + P 1(l – a 1) + P 2 a 2 = 0, (а) RA = [ P 1(l – a 1) + P 2 a 2]/ l. S mA = 0, RBl – P 1 a 1 – P 2(l – a 2) = 0, (б) RB = [ P 1 a 1 + P 2(l – a 2)]/ l. Уравнения (а) и (б) для вычисления вертикальных реакций имеют тот же вид, что и уравнения в балочной системе. Для вычисления распора запишем следующие уравнения: S x = 0, HA – HB = 0, HA = HB = H. S mC пр = 0, RBl 2 – P 2(l 2 – a 2) – HBf = 0, (в) HB = H = [ RBl 2 – P 2(l 2 – a 2)]/ f, или:
В выражении (3.1) МС бал представляет собой изгибающий момент в сечении С в балке, перекрывающей тот же пролет и воспринимающей заданную на трехшарнирную арку вертикальную нагрузку (рис. 3.3). Из формулы (3.1) следует, что величина распора Н обратно пропорциональна стреле подъема арки f.
Определение внутренних усилий в арке от вертикальной нагрузки При действии на арку только вертикальных нагрузок (рис. 3.4, а) изгибающий момент в сечении с абсциссой х равен: Mx = RAx – P 1(x - a 1) – P 2(x - a 2) – Hy, или: Мx = Mx бал - H ∙ y, (3.2) где Мх бал — изгибающий момент в балке (рис. 3.4, б) от той же нагрузки в сечении с абсциссой х (так называемый балочный момент). Формулой (3.2) удобно пользоваться при построении эпюры моментов в арке. Значения Мх бал непосредственно берут из эпюры моментов, построенной для балки. Величину распора находят по формуле (3.1). Полученная формула для Мх наглядно показывает уменьшение изгибающего момента в арке по сравнению с балкой, что подтверждает экономичность арочной конструкции по сравнению с балочной. Это видно из построений на рис. 3.4, г, где показано совмещение балочной эпюры моментов и кривой, соответствующей слагаемому Н∙у в формуле (3.1). На рис. 3.4, д показан вид эпюры моментов Мх в арке.
Аналогичные формулы можно получить для поперечной Qx и продольной Nx сил. Для этого спроецируем все приложенные слева от сечения n – n силы (рис. 3. 4, в) сначала на нормаль к оси арки в сечении с абсциссой х, а затем на касательную к ней:
Qx = (RA – P 1 – P 2)cosj x – H sinj x, Nx = + (RA – P 1 – P 2)sinj x + H cosj x. Нетрудно убедиться, что величина, стоящая в круглых скобках в записанных выше выражениях, представляет собой величину поперечной силы в балке в сечении с той же абсциссой х; тогда эти формулы примут вид: Qx = Qx бал cosj x - Н sinj x, (3.3) Nx = Qx бал sinj x + H cosj x. (3.4) Отметим, что в арке принято считать N > 0 при сжатии. Рациональная ось арки Из формулы (3.2) следует, что в том случае, когда очертание оси арки совпадает с очертаниями балочной эпюры моментов М бал, называемой кривой давления, т. е. если
то в такой арке изгибающий момент Мх = 0.
Уравнение (3.5) называют уравнением рациональной оси арки. На рис. 3. 5, в приведены очертания арок с рациональной осью для различных случаев нагружения. Пример 3.1 Для заданной трехшарнирной арки с размерами, показанными на рис. 3. 6, вычислить значения внутренних усилий в сечениях m и n. Построить эпюры внутренних усилий. Уравнение оси арки – квадратная парабола с началом координат в точке А:
1. Определяем опорные реакции: S mA = q 6×3 + P∙ 9 – RB 12 = 0. RB = 6 кН. S mB = q 6×9 + P∙ 3 – RA 12 = 0. RA = 10 кН. H = MC бал/ f = (RB 6 – P∙ 3)/4 = 6 кН. 2. Строим эпюры Qх бал и Мх бал. 3. По формуле (3.2) вычисляем значения Мх, получив предварительно ординаты заданных сечений m и n:
4. Вычисляем Qm и Qn, используя формулу (3.3) Qm=Qm балcosj m - H sinj m Для вычисления тригонометрических функций воспользуемся следующими математическими соотношениями:
тогда
Аналогично: sinj n = - 0,555, cosj n = 0,832. Подсчитаем значения Q в заданных сечениях: Qm = Qm балcosj m - H sinj m = 4×0,832 – 6×0,555 = 0. В сечении n эпюра Q бал имеет разрыв, аналогично будет разрыв и в эпюре поперечных сил арки. Поэтому необходимо подсчитать поперечную силу слева и справа от сечения:
Одновременно найдем поперечные силы в опорных сечениях А и В.
QA = 10×0,6 – 6×0,8 = 1,2 кН; QB = -6×0,6–6(-0,8) = 1,2 кН. QC = - 2×1 = - 2 кН.
5. Вычисляем продольные усилия по формуле (3.4): Nm = Qm балsinj m + H cosj m = 4×0,555 + 6×0,832 = 7,218 кН, Nn л = (-2)×(- 0,555) + 6×0,832 = 6,108 кН, Nn пр = (- 6)×(- 0,555) + 6×0,832 = 8,328кН, В опорных сечениях: NA = 10×0,8 + 6×0,6 = 11,6 кН, NВ = (-6)×(-0,8) + 6×0,6 = 8,4 кН. 6. Сводим полученные значения в таблицу и строим эпюры внутренних усилий в арке (рис. 3. 6).
Пример 3.2 Для заданной трехшарнирной рамы с размерами и нагрузкой, показанными на рис. 3. 7, а, построить эпюры внутренних усилий. 1. Определяем опорные реакции: S mA = - q 12×18 - P∙ 3 + RB 24 = 0. RВ = 10,25 кН. S mB = q 12×6 + P∙ 21 – RA 24 = 0. RА = 11,75 кН. H = MC бал/ f = (RА ∙12 – P∙ 9)/6 = 8.5 кН. 2. Строим эпюры Qх бал и Мх бал (рис. 3. 7, б).
3. По формулам (3.2), (3.3), (3.4) вычисляем значения внутренних усилий, используя табличную форму.
Qk=Qk балcosj k - H sinj k (3.3) Nk = Qk балsinj k + H cosj k (3.4)
В таблицу заносим опорные точки, точки приложения сосредоточенных сил, начала и конца распределенной нагрузки и узлы рамы. В точках приложения сосредоточенных сил в узлах необходимо находить по два усилия (слева и справа от сечения).
Используя данные 8, 12 и 15 столбцов строим эпюры внутренних усилий в трехшарнирной раме (рис. 3.8)
3.2 Расчет арок на подвижную нагрузку
Линии влияния опорных реакций
Для определения вида линии влияния реакции RА составим следующее уравнение равновесия S mB = 0, RА∙l – P (l – x) = 0. Тогда линия влияния левой реакции л. в. RА = Выражение для линии влияния реакцию RВ определим из уравнения S mA = 0, RВ∙l – P∙ x = 0. В результате: л. в. RВ = Линии влияния реакций RА и RВ показаны на рис. 3.8. Отметим, что линии влияния вертикальных реакций в арке те же, что и в однопролетной балке и в ферме. Поскольку выражение горизонтальной реакции (распора) связано со значением балочного изгибающего момента в точке С Сила Р = 1 справа от точки С. Рассмотрим равновесие левой части арки.
Получили уравнение правой ветви линии влияния H. Аналогично получим уравнение левой ветви - сила Р = 1 слева от точки С.
Линия влияния Н показана на рис. (3.8).
Построение линии влияния изгибающего момента Воспользуемся выражением для изгибающего момента в арке Mк = Mкб – Н∙ук. Очевидно, что справедливо следующее утверждение л.в. Mк = л.в. Mкб – (л.в.Н)ук, то есть линию влияния момента в арке можно построить методом наложения двух линий влияния - Mкб и Н∙ук. Поступаем следующим образом. 1. Вверх от оси строим линию влияния Mкб (на рис. 3.9 показана сплошной линией). 2. На той же оси откладываем ординаты линии влияния Н, умноженные на координату точки «к» ук (пунктирная линия). Для этого достаточно построить левую ветвь л.в. Н, умножив ее ординаты на ук, Правая ветвь будет представлена прямой, соединяющей конец левой ветви (проекция т. С) с нулевой точкой на правой опорной вертикали (проекция т. В). 3. В результате получаем разность ординат линий влияния Mкб и Нук (заштрихованная область на рис. 3.9 и представляет собой линию влияния Mк). Точка F′ – нулевая точка линии влияния Mк. Положение нулевой точки F′ можно найти графическим построением на чертеже арки (графически). Нулевое значение Mк получается при положении единичной силы в интервале между сечением к и ключевым шарниром С. Так как единичная сила приложена к левому диску арка, линия действия правой реакции В должна проходить через центр ключевого шарнира, поскольку
Поскольку единичная сила правее сечения «к», то для выполнения условия, что Mк = 0, реакция А должна действовать по линии Ак. Проводим линии Ак и ВС, под точкой пересечения которых и находится нулевая точка F′. Для построения линии влияния Mк способом нулевой точки откладываем на левой опорной вертикали ординату 1∙ ак, далее соединяем ее с нулевой точкой F′ - получаем 1-ю правую ветвь. Проводя вертикаль через шарнир С получаем границу 1-й и 2-й правых ветвей (то есть правая ветвь представляет собой ломаную линию). Левую ветвь находим по 1-й правой ветви, соединяя ее начало с левой опорной точкой. Ординату нулевой точки можно определить аналитически. Она равна (без вывода)
Построение линии влияния поперечной силы. Воспользуемся выражением для поперечной силы в арке Qк = Qкб cos j к– Н sin j к. (3.3) Поскольку для заданного сечения величины cos j к и sin j к постоянны, справедливо следующее утверждение л.в. Qк = (л.в. Qкб) cos j к – (л.в.Н) sin j к. То есть для построения линию влияния поперечной силы в арке можно воспользоваться методом наложения линий влияния Qкб и Н, умноженных на значения соответствующих тригонометрических функций. Поступаем следующим образом (рис. 3.10). 1. Строим линию влияния Qкбcos j к для сечения «к». 2. Вверх от оси откладываем ординаты линии влияния Н sin j к, которые получаем по левой ветви, ордината которой на правой опоре равна (l 2/ f) sin j к. 3. Отмечаем (штрихуем) ординаты, соответствующие выражению (3.3).
Отметим, что в пересечении левой ветви л. в. Н sin j к с правой ветвью л. в. Qкбcos j к находится нулевая точка F 1′, положение которой можно установить графически по чертежу арки. Действительно, если сила Р = 1 находится между точками к и С, то слева от точки «к» будет действовать только реакция А и для того, чтобы в сечении «к» выполнялось условие В то же время, линия действия реакции В будет направлена вдоль прямой ВС. На пересечении этих прямых находится нулевая точка F 1. Для построения линии влияния поперечной силы в арке методом нулевой точки достаточно в сечении «к» провести касательную к оси арки направить реакцию А по этой касательной до пересечения с прямой, соединяющей шарниры С и В и получить положение нулевой точки. Далее, отложить на левой опорной вертикали ординату cos j к и провести 1-ю правую ветвь через точку F 1′. Проводя вертикаль через шарнир С получаем границу 1-й и 2-й правых ветвей. Затем проводим левую ветвь, которая параллельна 1-й правой ветви (рис. 3.10). Положение нулевой точки F 1 можно определить аналитически
Построение линии влияния продольной силы.
По аналогии с построением линии влияния поперечной силы, для построения линии влияния продольной силы можно применить метод наложения и метод нулевой точки. Для метода наложения необходимо воспользоваться выражением для продольной силы в арке Nк = – Qкб sin j к – Н cos j к, (3.4) тогда: л.в. Nк = (л.в. Qкб) sin j к + (л.в.Н) cos j к. Здесь мы учли, что сжимающая сила в арке считается положительной. Воспользуемся методом наложения (рис. 3.11). 1. Строим линию влияния Qкб sin j к. 2. От оси вниз строим линию влияния Н cos j к по левой ветви (пунктирная линия). 3. Складываем ординаты построенных линий влияния. Если продолжить правую ветвь (л.в.Н) cos j к < |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

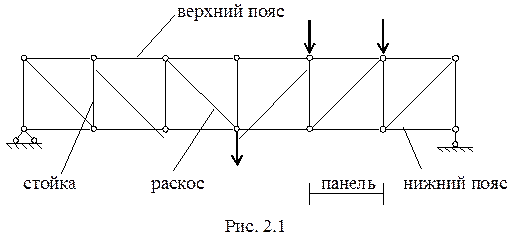
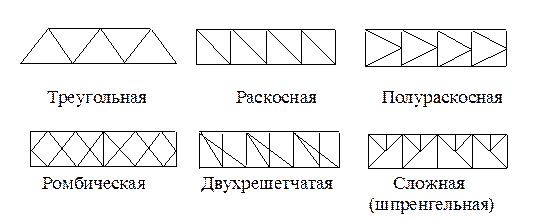



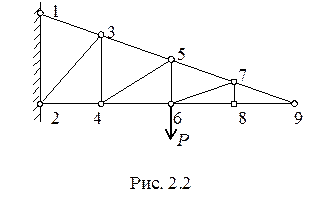



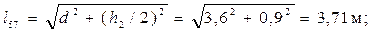


 тогда уравнение правой ветви примет вид линии влияния реакции Ra, умноженной на множитель 2 d / r 1:
тогда уравнение правой ветви примет вид линии влияния реакции Ra, умноженной на множитель 2 d / r 1: (л. в. RА) =
(л. в. RА) =  (л. в. RА) = -
(л. в. RА) = - 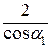 (л. в. RА).
(л. в. RА). (л. в. RВ) =
(л. в. RВ) =  (л. в. RА) =
(л. в. RА) = 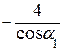 (л. в. RА).
(л. в. RА). (л. в. RА) =
(л. в. RА) =  (л. в. RА) =
(л. в. RА) =  (л. в. RА).
(л. в. RА). (л. в. RВ) =
(л. в. RВ) =  (л. в. RВ).
(л. в. RВ).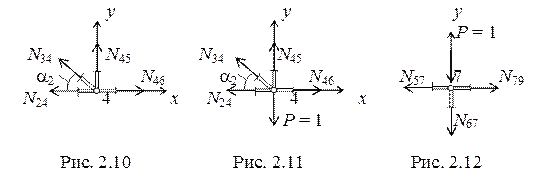
 sina2 + 1 =
sina2 + 1 =  .
.

 (3.1)
(3.1)
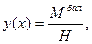 (3.5)
(3.5)
 , где l = 12 м, f = 4 м.
, где l = 12 м, f = 4 м.


 ;
;
 ,
,
 ,
, 
 ,
, ,
, 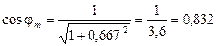 .
.




 (3.2)
(3.2)

 . (3.6)
. (3.6) . (3.7)
. (3.7) , его линия влияния будет иметь две ветви.
, его линия влияния будет иметь две ветви. , RА∙l 1 – H∙f = 0. Откуда
, RА∙l 1 – H∙f = 0. Откуда . (3.8)
. (3.8) , RВ∙l 2 - H∙f = 0. Тогда
, RВ∙l 2 - H∙f = 0. Тогда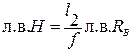 . (3.8)′
. (3.8)′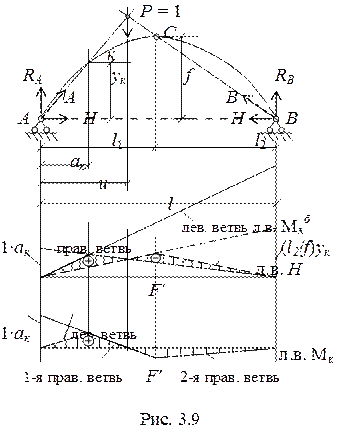
 (3.9)
(3.9)
 , реакция должна быть параллельна касательной к оси арки в сечении «к».
, реакция должна быть параллельна касательной к оси арки в сечении «к».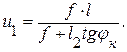 (3.10)
(3.10)


