
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическая цепь с емкостьюСодержание книги
Поиск на нашем сайте
Элементом электрической цепи, обладающей значительной емкостью, является конденсатор. Конструктивно конденсатор представляет собой две пластины с большой (по сравнению с зазором между пластинами) поверхностью, разделенные между собой диэлектриком. Емкость С конденсатора определяет тот электрический заряд, который накапливается на пластинах при разности потенциала между ними в 1В. Размерность емкости С – (Ф, фарад). 1мкФ=10-6Ф (микрофарада) 1пФ=10-12Ф (пикафарада) 1нФ=10-9Ф (нанафарада). Зазор в конденсаторе не является препятствием для прохождения переменного тока, так как синусоидальное напряжение периодически меняется по направлению, следовательно, так же непрерывно меняется заряд на обкладках конденсатора (конденсатор перезаряжается). Реально емкостью обладают любые два проводника, расположенные недалеко друг от друга, но при малой поверхности (по сравнению с зазором) их емкость не велика и ею пренебрегают.
Пусть к цепи с конденсатором, емкость которого С, приложено синусоидальное напряжение u = Umsinωt. Под действием этого напряжения в цепи создается синусоидальный ток i и на каждой пластине скапливается заряд Q=Cuc, где uc – падение напряжения на конденсаторе. Рис.15 Выбираем условные положительные направления тока, напряжения и ЭДС. По второму закону Кирхгофа u=uc, тогда заряд на конденсаторе Q=Cuc=СUm sinω t. Ток в цепи представляет собой изменение заряда во времени: i=dQ/dt=ωCUmcos ωt=ωCUmsin(ωt+π/2), i=Imsin(ωt+π/2), Im=Um /(1/ωC). Таким образом, ток в цепи с конденсатором так же изменяется по синусоидальному закону и опережает напряжение на угол π/2 (рис.16). Знаменатель 1/ ω C имеет размерность сопротивления – это емкостное сопротивление хс:
Следовательно получаем Im = Um/xс –для амплитудного значение тока; I = U/xс –для действующего значения тока. В комплексной форме: U =Uej 0 = U, I =Ie jπ/2=jI. Индуктивное сопротивление в комплексной форме
На векторной диаграмме вектор напряжения отстает от вектора тока на угол π/2 (рис.17).
Рис.17
Электрическая цепь при последовательном соединение r, L и С элементов
Рис.18
К электроцепи (рис.18) подводится напряжение u, под действием которого по цепи течет ток i = Imsinωt. По второму закону Кирхгофа запишется уравнение:
где В показательной форме где
Рис.19
Мгновенное значение напряжения u=Umsin(ωt+φ). Вывод: напряжение опережает ток на фазный угол φ. В зависимости от соотношения сопротивлений ХL и XC цепь имеет характер: а) индуктивный, если ХL > XC, при этом φ >0; б) емкостный, если ХL < XC,при этом φ<0 в) резонанс, если ХL = XC, при этом φ=0. На рис. 20 приведены векторные диаграммы напряжений и синусоиды напряжений и токов, соответствующие трем выше изложенным режимам.
Рис.20
Резонансные явления
Под резонансом понимают явление резкого возрастания амплитуды колебания, когда частота внешнего возмущения и силы совпадает с частотой собственных колебаний системы. Имеем цепь, которая кроме активного сопротивления содержит и реактивные составляющие. Несмотря на это цепь, имеет активный характер, то есть ток и напряжение совпадают по фазе. Тогда в этой цепи наблюдается резонанс.
Условия резонанса:
i=Im sinω t, u=Um sin(ω t+ φ), I =I, U =Uejφ, Z =Zejφ=R+j(xL-xC)=R+jx. При резонансе: xL=xC, ωL=1/ωC, xL-xC= 0, x=0, φ=0 При резонансе полное комплексное сопротивление является вещественным числом Z=R. Для проводимости: Y =Ye-jφ=g-j(bL-bC)=g-jb, где bL=bC, b= 0, φ=0, Y=g.
Резонанс напряжений.
Резонанс напряжений возможен в цепях с последовательно соединенными катушкой индуктивности и конденсатором. Если xL=xC, то есть ω0 L= 1 / ω0 C, где ω0 – резонансная частота или собственная частота цепи.
Q – определяет качество конура. Q=200-500 для радиотехнических контуров. Так как сопротивление и напряжение находятся в прямо пропорциональной зависимости, то UL=UC, отсюда название – резонанс напряжений. Напряжение на конденсаторе и катушке индуктивности взаимно компенсируют друг друга при резонансе, причем эти два напряжения при резонансе больше чем напряжение источника.
Для действующих значений: UL=xLI, UC=xCI, UR=RI При резонансе UL=ρI, UC=ρI, U= rI,
Добротность Q определяет качество контура. Для радиотехнических контуров Q =200~500. Добротность Q определяет во сколько раз напряжение на каждом реактивном элементе больше чем напряжение, подведенное к цепи. Ток при резонансе имеет максимальное значение. Так как сопротивление цепи определяется только активной составляющее, следовательно, минимально, а как известно сопротивление и ток находятся в обратно пропорциональной зависимости. I=U/R При резонансе происходит взаимный обмен энергией между катушкой и конденсатором. Поэтому реактивная составляющая мощности равна нулю. Коэффициент мощности при резонансе имеет максимальное значение. Резонанс токов.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 936; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.71 (0.007 с.) |

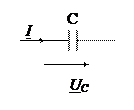 В простейшем случае рассматривают идеальный конденсатор с емкостью С =const, его сопротивление R= 0, индуктивность L= 0.
В простейшем случае рассматривают идеальный конденсатор с емкостью С =const, его сопротивление R= 0, индуктивность L= 0.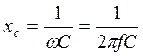 .
.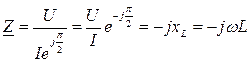 – отрицательное мнимое число.
– отрицательное мнимое число.


 ,
,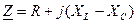 ;
; 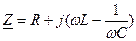 .
. ,
,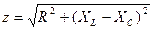 и
и  определяются из треугольника сопротивлений (рис.19).
определяются из треугольника сопротивлений (рис.19).
 , так как ψi =0.
, так как ψi =0. , U=zI
, U=zI
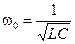 ,
,  - волновое сопротивление.
- волновое сопротивление.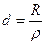 - характеризует насколько резко выражено явление резонанса в цепи.
- характеризует насколько резко выражено явление резонанса в цепи. - добротность определяет во сколько раз напряжение на каждом реактивном из реактивных элементов больше, чем подведенное к цепи напряжение.
- добротность определяет во сколько раз напряжение на каждом реактивном из реактивных элементов больше, чем подведенное к цепи напряжение.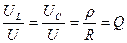 , если ρ ›› R, то UL и UC ›› U
, если ρ ›› R, то UL и UC ›› U


