
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что такое элемент сообщения и чем он характеризуется?Содержание книги
Поиск на нашем сайте
Информационный элемент – квант (неделимая часть информации). Что такое «бит» и какому сообщению соответствует 1 бит? Бит – это неделимый элемент, получаемый двоичными единицами. Чему равно количество информации по Хартли? I = log2 Q = Nlog2 h (бит) 1.5 Какое количество информации I содержат сообщения: а) 10010101, б) 1101, в) 1234567890, 1.6 Задана информационная емкость системы в виде десятичного числа Q=1000 а) Определите потенциальное количество информации I в такой системе. б) Закодируйте заданное число по двоичной системе (h=2). Найдите необходимое число разрядов N. в) Сделайте выводы. а) I=N log2 1000=10 б) 1111101000, N=10 Опишите сообщение, для которого количество информации определяется энтропией. Cообщение из N элементов, каждый из которых может принимать любое из m состояний х1,...хк,...хm с вероятностью р1,.. рк,..рm. Опишите свойства энтропии. Энтропия характеризуется следующими свойствами: 1. Энтропия всегда неотрицательна. 2. Энтропия равна 0, когда одно событие имеет вероятность 1, остальные – 0, т.е. этот опыт не несет новой информации. 3. Энтропия имеет наибольшее значение при р1= р2 =.. рm= 1/m, при этом Нmax= - log21/m = log 2m. 1.9 Что означает условие m=h? Очевидно, если m=h, то удельная информативность по Хартли и энтропия Шеннона совпадают. Это совпадение будет означать о полном использовании информационной емкости системы. В случае неравных вероятностей количество информации по Шеннону меньше информационной емкости системы. 1.10 Чему равна энтропия двух неравновероятных состояний одного элемента (h=2) H= Чему будет равна энтропия по пункту 1.10 при равной вероятности состояний? m=h если p1=p2 Icр=-(0.5 log2 0.5+0.5 log20.5)=1 бит. 1.12 Чему будет равна энтропия по пункту 1.10, если
1.13 Чему будет равна энтропия по пункту 1.10, если
1 .14 Нарисуйте график H(p) для случая п.1.10.
Ответы к лекции №2 2.1 Какие сигналы называются детерминированными? Нарисуйте примеры. Детерминированный сигнал – это сигнал, линейного значения которого в любой момент времени известны.
2.2 Какие сигналы называют случайными? Нарисуйте примеры. Случайные сигналы – это сигналы мгновенного значения которых не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. 2.3 Какие сигналы называют непрерывными.(аналоговыми)? Нарисуйте примеры с учетом п.п.2.1 и 2.2. Непрерывный сигнал – это сигнал, который может принимать лишь конечное число значений.Непрерывные сигналы описываются непрерывными функциями х(t) Переход от аналогового представления к цифровому дает значительные преимущества при передаче, хранении и обработке информации и связан с квантованием (дискретизацией) сигнала х(t) по времени и уровню.
Рис.3 Непрерывная функция непрерывного аргумента 2.4 Какие сигналы являются дискретными? Нарисуйте примеры Дискретный сигнал – это сигнал, который может принимать лишь конечное число значений.Рис.4 Дискретная функция дискретного аргумента
Как осуществляется квантование по уровню? Квантование сигнала х(t) по уровню состоит в преобразовании непрерывных значений х(ti) в моменты отсчета ti в дискретные хk (рис.5). В результате непрерывное множество значений х(ti) в диапазоне от хmin до хmax превращается в дискретное множество хk уровней квантования, где k=1,... m.
Рис.5 2.6 Как выглядит квантованный по времени сигнал? Нарисуйте примеры.
Какие задачи возникают при дискретизации непрерывных сообщений? При дискретизации решается проблема, каков должен быть шаг дискретизации Оптимальным является шаг, который обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве выборок. Избыточные отсчеты не увеличивают точность восстановления, загружают тракт передачи информации, уменьшают производительность обработки данных в ЭВМ и т.д. Сокращение избыточных данных - актуальная задача и может решаться в процессе дискретизации. Какие принципиальные недостатки свойственны модели непрерывных сообщений с ограниченным спектром? Реальные сигналы имеют конечную длительность. Спектр таких сигналов не ограничен, поэтому применение теоремы Котельникова приводит к погрешностям восстановления и проблемам в выборе шага квантования.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.123.220 (0.009 с.) |

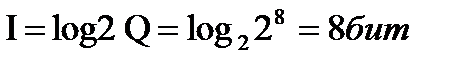

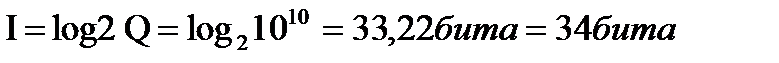
 999/
999/ = -(p1log2 p1+ p2log2 p2)
= -(p1log2 p1+ p2log2 p2) ?
?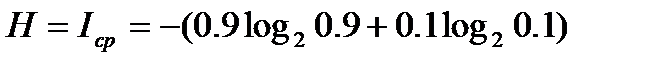 =0.47
=0.47 или
или  ?
?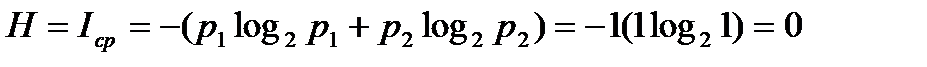







 .
.


