
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние высших пространственных гармоник на электромагнитный момент АД.Содержание книги
Поиск на нашем сайте
Высшие гармоники делят на временные и пространственные. Временные гармоники обусловлены несинусоидальным распределением магнитного поля по длине окружности статора. Обмотка статора обычно состоит из отдельных катушек, число которых ограниченно, поэтому форма магнитного поля представляет ступенчатую кривую, которая является функцией пространственной координаты. Эту сложную кривую раскладывают в ряд Фурье и помимо основной получается ряд высших пространственных гармоник которые являются функцией пространственной координаты: 1) Асинхронные 2) Синхронные 3) Вибрационные Асинхронные возникают вследствие взаимодействия магнитных полей высших гармоник с токами ротора высших гармоник. Высшие гармоники тока создают свои вращающиеся магнитные поля, которые пересекают проводники ротора и в них наводится ЭДС соответствующей частоты. Под ее действием протекают токи и взаимодействие этих токов с полем высших гармоник создает вращающие моменты высших гармоник. Полюсное деление для высшей гармоники в ν раз меньше, чем для основной гармоники.
Поле высших гармоник пересекая обмотку ротора наводят в них ЭДС, которая зависит от скольжения.
С такой же частотой протекают и токи от высших гармоник. Токи ротора тоже создают вращающееся магнитное поле, которое вращается относительно ротора со скоростью.
Сам ротор вращается со скоростью n=n0(1-s). Следовательно магнитное поле высших гармоник вращающееся со скоростью:
Магнитное поле ротора высших гармоник вращающееся в пространстве с той же скоростью, что и магнитное поле высших гармоник обмотки статора. При взаимодействии магнитных полей высших гармоник с токами высших гармоник того же порядка, возникают отличные от 0 моменты. При взаимодействии гармоник различных порядков возникают моменты среднее значение которых за период = 0. Если порядок гармоники выражается 6к+1, к=1,2.., то магнитное поле вращается в том же направлении, что и основное. Если порядок 6к-1, то магнитное поле гармоники вращается в противоположную сторону. Если порядок 6к гармоники отсутствуют. 1) 6а+1. Основное поле создает основной момент, который изображается:
Скольжение, которое соответствует синхронной скорости высшей гармоники относительно первой
Если ротор вращается со скоростью n0 т.е. со скоростью вращающего поля высшей гармоники. Если со s=1- Если ротор вращается со скоростью превышающей скорость вращения ν гармоники, то по отношению к этой гармонике машина работает в режиме генератора. Б) 6а-1. Эта гармоника создает вращающееся поле с противоположным направлением, т.е.
Если ротор вращается с этой скоростью и со:
то ротор находится в синхронизме с полем этой гармоники. Если убавить обороты ротора или увеличить скольжение, то ротор будет отставать от магнитного поля этой гармоники, т.е. машина будет работать в режиме двигателя и в режиме электромагнитного тормоза. При этом момент – положительный. Если ротор вращается в сторону поля с большой скоростью, то по отношению к этой гармонике машина будет работать в режиме генератора. Наличие высших гармоник приводит к тому, что в области s=1 наблюдается провал и если в момент пуска Мсопр>Мвр двигатель затормаживается и будет работать с низкой скоростью при высоких s, что ведет к перегреву.
Рассмотренные высшие гармоники появляются в следствии конечного числа катушек в обмотке статора. Помимо этих гармоник на работу машины оказывают влияние зубцовые гармоники, которые объясняются наличием зубцов. Наличие зубцов приводит к тому, что в кривой индукции появляются провалы, которые эквивалентны появлению высшей гармоники со знаком «-» Порядок зубцовой гармоники зависит от z1.
Особеностью гармоник зубцового порядка является то, что обмоточный коэффициент гармоник по величине равен Коб для 1 гармоники, поэтому он не может быть уменьшен за счет укорочения и распределения обмотки.
y- шаг обмотки – расстояние между сторонами катушки, измеряется величиной зубцов (пазов), а каждому зубцу соответствует зубцовое деление
- в шаге целое число зубцовых делений. Т.к. в выражение Куз входит выражение
Для зубцовых гармоник Коб равен Коб для 1 гармоники 2) Синхр. моменты возникают в том случае, если поле зубцовых гармоник статора вращающихся в пространстве с той же скоростью, что и магнитное поле зубцовых гармоник ротора т.е. в машине возникает 2 магнитных поля вращаются с одной и той же скоростью. Взаимодействие этих полей создает электромагнитный момент, который может быть «+» и «-». Поскольку частота вращения зависит от порядка гармоники, то
Условие возникновение синхронного момента:
Машины с одинаковым z1 и z2 не изготавливаются т.к. в момент пуска, когда между ними возникает сила тяжения и ротор не может раскрутится. Если z1-z2= Так же обычно избегают нечетного числа зубцов хотя бы на статоре или роторе. 3) Эти моменты обусловлены зубчатостью статора или ротора. При вращении ротора его зубцы периодически совпадают с зубцами статора, при этом возникает сила магнитного тяжения между статором и ротором. Эта сила будет компенсироваться за счет подшипников. Т.к. число пазов статора и ротора различно, то сила тяжения перемещается по окружности статора со скоростью пропорциональной разнице z1 и z2. Описанные процессы приводят к возникновению шумов вибрациям, износу подшипников. Для борьбы с паразитными моментами используют методы: 1) Разумно определяют распределение и ускорение обмотки, с таким расчетом, чтобы обеспечить максимальную величину момента от 1 гармоники и минимальную величину от высших гармоник. Каждая катушечная группа состоит из q катушек. Число q обычно (2-6), при этом уменьшается амплитуда простых гармоник. В большинстве случаев обмотки выполняются двухслойными, что позволяет укорачивать шаг, что так же приводит к уменьшению амплитуды МДС высших гармоник. 2) Для подавления гармоник зубцового порядка обычно на роторе выполняется скос паза, причем 3) Для уменьшения вибрационных моментов число зубцов статора и ротора выбирается в определенных соотношениях
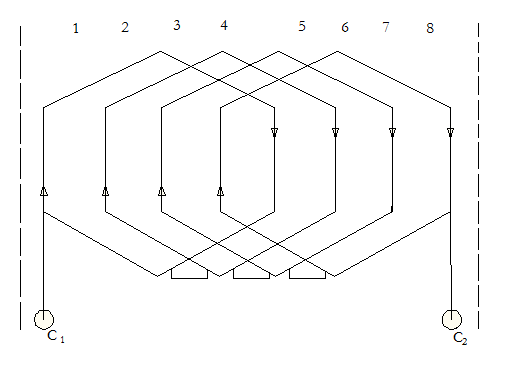
Двухфазная равносекционная однослойная
В этом случае получается очень низкий Коб1.
Обычно обмоткой заполняется
Двухфазная равносекционная однослойная
Обмотки разных фаз смещены на 90 эл.град
Двухслойные обмотки позволяют за счет укорочения уменьшить амплитуды высших гармоник.
К недостаткам двухслойных обмоток относится сложность технологического вычисления, т.к. приходится укладывать нижний слой под верхним. Поэтому в последнее время разработаны частично-двухслойные обмотки. Синусные обмотки. В ряде машин требуется очень малый процент пространственных гармоник. В этих случаях применяются синусные обмотки, в которых число витков в различных катушках различно, причем число витков распространяется по синусоидальному закону.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.66.57 (0.012 с.) |

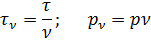
 Т.к. по обмотке статора протекает ток одной и той же частоты, то для всех простых гармоник частота тока получается одинаковая, следовательно частота вращения поля высших гармоник
Т.к. по обмотке статора протекает ток одной и той же частоты, то для всех простых гармоник частота тока получается одинаковая, следовательно частота вращения поля высших гармоник 



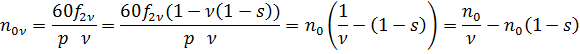

 Высшая гармоника создает вращающееся поле:
Высшая гармоника создает вращающееся поле: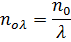
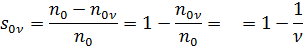
 , то ротор находится в синхронизме с полем высшей гармоники и момент в этом случае = 0. Если ротор вращается с меньшей скоростью, чем поле ν гармоники или при большем скольжении, то по отношению к ν гармоники машина работает сначала в режиме двигателя, а затем в режиме электромагнитного тормоза. В этих режимах момент «+».
, то ротор находится в синхронизме с полем высшей гармоники и момент в этом случае = 0. Если ротор вращается с меньшей скоростью, чем поле ν гармоники или при большем скольжении, то по отношению к ν гармоники машина работает сначала в режиме двигателя, а затем в режиме электромагнитного тормоза. В этих режимах момент «+».
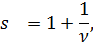
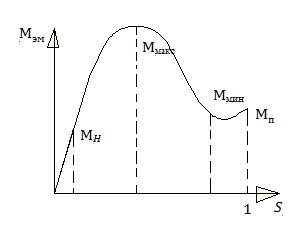 Помимо 5 и 7 в машине присутствуют и другие высшие гармоники действие которых аналогично. Все эти гармоники вызывают уменьшение момента в зоне скольжения 0,75 – 0,85. В результате реальная зависимость М=f(s) отличается от зависимости для первой гармоники.
Помимо 5 и 7 в машине присутствуют и другие высшие гармоники действие которых аналогично. Все эти гармоники вызывают уменьшение момента в зоне скольжения 0,75 – 0,85. В результате реальная зависимость М=f(s) отличается от зависимости для первой гармоники.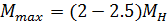


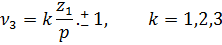

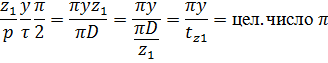
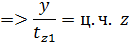
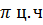 , то для зубцовых гармоник Ку будет отличатся от Ку для 1–ой гармоники только знаком.
, то для зубцовых гармоник Ку будет отличатся от Ку для 1–ой гармоники только знаком.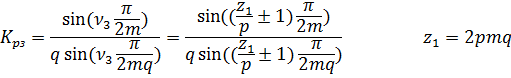
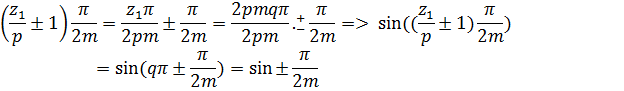
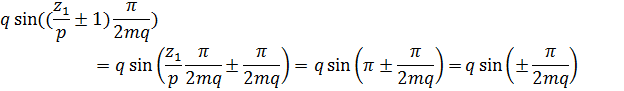
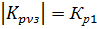
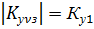
 .
.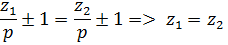
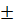 2p. То в машине возникают синхронные моменты поэтому такое соотношение также не допустимо.
2p. То в машине возникают синхронные моменты поэтому такое соотношение также не допустимо.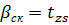 . При скосе паза ротора, один конец проводника находится в зоне действия магнитного поля одного знака, а противоположный конец в зоне действия другого. Суммарная ЭДС от гармоник зубцового порядка будет равна 0, следовательно, ток тоже будет близок к нулю.
. При скосе паза ротора, один конец проводника находится в зоне действия магнитного поля одного знака, а противоположный конец в зоне действия другого. Суммарная ЭДС от гармоник зубцового порядка будет равна 0, следовательно, ток тоже будет близок к нулю.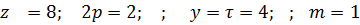

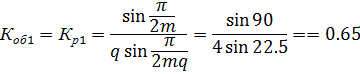
 , а
, а 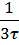 заполняется пусковой обмоткой
заполняется пусковой обмоткой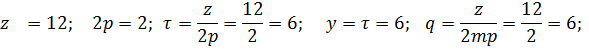
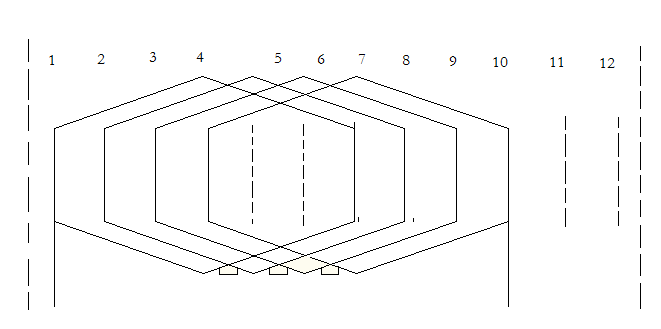

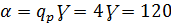
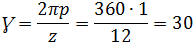
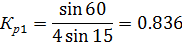
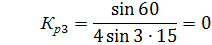
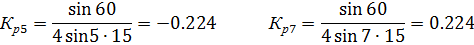
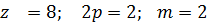
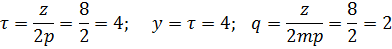
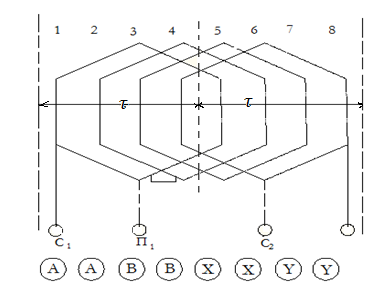


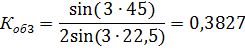


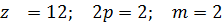
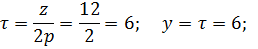
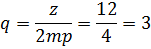
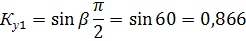

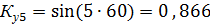
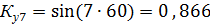
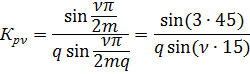
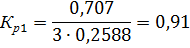
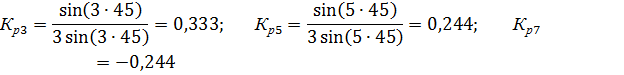
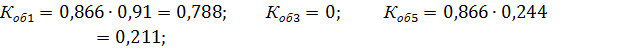
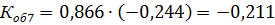 т.о. за счет укорочения шага обмотки удается удалить 3-ю и снизить 5 и 7-ю
т.о. за счет укорочения шага обмотки удается удалить 3-ю и снизить 5 и 7-ю


