
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные состояния поляризацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если для световой волны задано направление распространения, то в общем случае её можно представить как суперпозицию двух линейно поляризованных волн, для которых направления поляризации взаимно перпендикулярны. Для естественного света характерно хаотическое изменение амплитуд и фаз каждой из этих волн. Если же амплитуды обеих волн постоянны, а фазы изменяются по гармоническому закону, то в зависимости от разности фаз будут наблюдаться различные состояния поляризации волны. Рассмотрим подобную ситуацию более подробно. Пусть вдоль оси Z распространяются две монохроматические линейно поляризованные волны, для которых
где В зависимости от соотношения амплитуд Пусть начальные значения фаз равны друг другу:
y
-
- Рис.1а.
Из уравнений (1) и (2) следует, что 2) Разность фаз равна
y
-
-
Рис.1б. 3) Разность фаз равна В этом случае колебания в волне, поляризованной вдоль оси x, опережают колебания в волне, поляризованной вдоль оси y на
-
Рис.1в
В этом случае 4) Разность фаз равна Волна, поляризованная вдоль оси x, отстает на Результаты будут аналогичны результатам, полученным в п.3, только вектор
-
-
Рис.1г
y y
Рис.2в. Рис.2. Поляризация волны при произвольных значениях разности фаз
5) В общем случае, для произвольного соотношения начальных фаз Направление вращения результирующего вектора зависит только от знака разности фаз
Разобранные выше случаи позволяют сформулировать следующее правило (с учётом периодичности разность фаз а) б) 0 < в) Таким образом, в общем случае вдоль оси будет распространяться эллиптически поляризованная волна (линейная поляризация есть частный случай эллиптической поляризации, когда размер одной из полуосей эллипса равен нулю). Из приведённых соотношений следует, что волну с произвольной поляризацией можно всегда представить как сумму двух линейно поляризованных волн с взаимно перпендикулярными направлениями поляризации. В свою очередь, любую линейно поляризованную волну можно представить как сумму двух циклически поляризованных волн с левой и правой поляризациями. Обратим внимание на следующий факт: хотя значение разности фаз существенным образом влияет на структуру результирующем волны, интенсивность волны не зависит от Примечание. Под интенсивностью понимают среднее значение потока энергии (вектора Умова-Пойнтинга), пропорционального
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , а плоскости поляризации взаимно перпендикулярны. Тогда для компонент результирующего поля
, а плоскости поляризации взаимно перпендикулярны. Тогда для компонент результирующего поля  волны можно записать:
волны можно записать: , (1)
, (1) , (2)
, (2) - волновое число;
- волновое число; 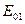 и
и  - амплитуды каждой из волн;
- амплитуды каждой из волн; 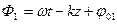 и
и 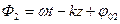 - фазы каждой из волн;
- фазы каждой из волн;  и
и  - начальные значения фаз каждой из волн.
- начальные значения фаз каждой из волн.



 . В этом случае результирующая волна оказывается линейно поляризованной с амплитудой равной
. В этом случае результирующая волна оказывается линейно поляризованной с амплитудой равной  . При этом её плоскость поляризации образует с направлением x угол, тангенс которого равен
. При этом её плоскость поляризации образует с направлением x угол, тангенс которого равен  (рисунок 1а).
(рисунок 1а).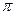 :
:  .
. В этом случае
В этом случае  и результирующая волна также будет линейно поляризованной. Её амплитуда равна
и результирующая волна также будет линейно поляризованной. Её амплитуда равна 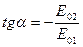 (рисунок 1б).
(рисунок 1б).
 :
:  .
. y
y
 . При этом вектор
. При этом вектор  результирующего поля в любой точке оси Z будет вращаться в плоскости Z=const против часовой стрелки (наблюдение ведётся навстречу волне), а конец вектора будет описывать эллипс с полуосями
результирующего поля в любой точке оси Z будет вращаться в плоскости Z=const против часовой стрелки (наблюдение ведётся навстречу волне), а конец вектора будет описывать эллипс с полуосями  , то длина вектора
, то длина вектора  . Такую волну называют поляризованной по кругу, или циркулярно (циклически) поляризованной (круговая или циклическая поляризация), причём в данном случае говорят о левой круговой поляризации волны.
. Такую волну называют поляризованной по кругу, или циркулярно (циклически) поляризованной (круговая или циклическая поляризация), причём в данном случае говорят о левой круговой поляризации волны. :
:  .
. y
y
 y
y 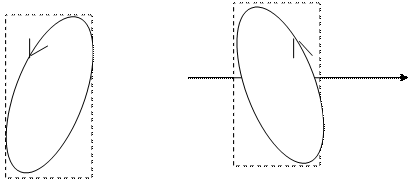


 Рис.2а. 0<
Рис.2а. 0<  <
<  Рис.2б.
Рис.2б.  <
< 
 и разностью фаз
и разностью фаз  .
. .
. :
: - линейно поляризованная волна,
- линейно поляризованная волна, ~
~  . Это связано с тем, что две волны со взаимно перпендикулярными направлениями поляризации не интерферируют друг с другом, т.е. интенсивность суммы таких волн равна сумме их интенсивностей.
. Это связано с тем, что две волны со взаимно перпендикулярными направлениями поляризации не интерферируют друг с другом, т.е. интенсивность суммы таких волн равна сумме их интенсивностей. . Поэтому, хотя амплитуда линейно поляризованной волны, равная
. Поэтому, хотя амплитуда линейно поляризованной волны, равная 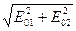 , больше амплитуды циклически поляризованной волны, у которой амплитуда постоянна и равна
, больше амплитуды циклически поляризованной волны, у которой амплитуда постоянна и равна  остаётся неизменным.
остаётся неизменным.


