
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В немагнитной среде с использованием законов АмпераСодержание книги
Поиск на нашем сайте И Био-Савара-Лапласа
Известно, что между проводниками, по которым протекают электрические токи, возникают механические силы, зависящие от величины этих токов и взаимного расположения проводников. Согласно современным физическим представлениям, эти силы обусловлены наличием в пространстве, окружающем токи, специфического силового поля, которое существует независимо от того, проявляется ли оно при воздействии на какие-либо другие токи или же в отсутствии таковых не проявляется ни в чем. Это поле сил называется магнитным полем тока, поскольку постоянные магниты создают такие же поля, как и электрические токи. Как показывают опыты, магнитное поле в любой точке пространства может быть охарактеризовано вектором индукции магнитного поля
где вектор
Многочисленные эксперименты по измерению сил, выраженных формулами (7) и (8) показали, что индукция
где магнитная постоянная μ0 =4∙10-7Гн/м; Формула (9) выражает закон Био-Савара-Лапласа. Если подставить в выражение (7) вместо индукции Индукция замкнутого витка с контуром l, по которому протекает ток I, определяется интегралом от выражения (9)
Если магнитное поле создается массивным проводником, по которому протекают постоянные токи с плотностью
Полная сила, действующая на массивный проводник, определяется интегралом по объему от выражения (11)
Когда индукция
Возможность такого обобщения обусловлена тем, что любой массивный проводник с током I можно разделить на совокупность отдельных тонких витков, сумма токов которых равна току I. При этом магнитное поле каждого составляющего тонкого витка может быть определено формулой (10), а сумма этих выражений при достаточно большем их количестве может быть преобразована к интегралу в формуле (13). Пусть теперь на тонкий виток с контуром l2 и током I2 действует магнитное поле витка с контуром l1 и током I1. Тогда сила
Подставляя сюда выражение (10) для
где Аналогичным образом можно получить выражение для силы, действующей со стороны витка 2 с током I2 на виток 1:
где R21=R12; вектор Для упрощения формул (14) и (15) и выяснения их физического смысла воспользуемся известной формулой векторного анализа
где Применяя эту формулу к двойному векторному произведению в (14), получим
Подставляя это соотношение в (14), представим силу
Внутренний интеграл во втором члене справа равен нулю, поскольку подынтегральное выражение является полным дифференциалом:
Поэтому выражение для силы
Тем же способом можно получить и выражение для силы
Поскольку
Такую же форму примет и выражение для силы s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Важно отметить, что принцип действия и противодействия соблюдается только для постоянных токов, которые в силу условия их непрерывности всегда являются замкнутыми. Чтобы это показать, рассмотрим взаимодействие замкнутого витка с контуром l1 и током I1 и незамкнутого элемента Силу
Силу
Первый член справа в (21) равен выражению (22) с противоположным знаком, и поэтому из-за второго члена в (21), в общем случае не равного нулю, принцип действия и противодействия не соблюдается. Он не будет соблюдаться и для двух взаимодействующих незамкнутых элементов, что иллюстрирует рис. 3. Элемент
Рис. 3. Взаимодействие незамкнутых элементов
Простые расчетные формулы для сил можно получить из приведенных выше формул общего вида только для отдельных частных случаев. В качестве простейшего примера приведем расчет сил взаимодействия между прямолинейными параллельными проводами, по которым протекают токи I1, I2 (рис. 4).
Рис. 4. Взаимодействие двух прямолинейных параллельных проводов
Будем считать провода бесконечно длинными. В этом случае индукция магнитного поля не зависит от координаты z, отсчитываемой вдоль проводов. Вектор индукции
Согласно рис. 4,
где d – расстояние между осями проводов. В результате
где Вектор индукции
Таким образом, если I1>0, I2>0, силы, действующие на провода, притягивают их друг к другу. Обычно для длинных проводов рассматриваются силы на единицу длины:
В двухпроводной линии электропередачи I1=I, I2=−I. Тогда
Из этих формул следует, что в двухпроводной линии электропередачи провода отталкиваются друг от друга. В общем случае при произвольных формах проводников расчет сил можно проводить на ЭВМ. При этом каждый контур разбивается на ряд отдельных малых элементов, после чего интегралы по замкнутым контурам заменяются конечными суммами. Расчет сил производится отдельно для каждой проекции вектора силы на оси координат. Аналогичным образом производится расчет сил, действующих на объемные (массивные) проводники. В этом случае объем каждого провода разбивается на совокупность отдельных малых элементов простой формы, в пределах которых плотность тока можно считать постоянной. После этого интегралы по объемам также заменяются конечными суммами. При этом следует отметить, что в случае массивных проводников может возникнуть необходимость предварительного расчета распределения плотности тока по объему проводника. Эта задача может быть решена с использованием теории постоянного электрического поля в проводящей среде путем решения краевой задачи для уравнения Лапласа относительно потенциала плотности тока.
|
|||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 с размерностью В×с/м2 (Т). В частном случае сила
с размерностью В×с/м2 (Т). В частном случае сила  , действующая на элемент dl тонкого провода, по которому протекает ток I, определяется формулой
, действующая на элемент dl тонкого провода, по которому протекает ток I, определяется формулой
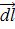 направлен вдоль тока I (т.е. вдоль тонкого провода),
направлен вдоль тока I (т.е. вдоль тонкого провода), 
 , создаваемая элементом тонкого провода dl, по которому протекает постоянный ток I, должна определяться по формуле
, создаваемая элементом тонкого провода dl, по которому протекает постоянный ток I, должна определяться по формуле
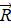 – вектор, направленный из точки расположения элемента dl в точку, где определяется индукция
– вектор, направленный из точки расположения элемента dl в точку, где определяется индукция 
 , меняющейся по объему проводника, то силу, действующую на элемент проводника dV, можно определить по формуле, аналогичной (8):
, меняющейся по объему проводника, то силу, действующую на элемент проводника dV, можно определить по формуле, аналогичной (8):


 , действующая со стороны витка 1 на виток 2, будет выражаться формулой
, действующая со стороны витка 1 на виток 2, будет выражаться формулой
 , получаем
, получаем
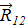 – вектор, направленный из произвольной точки на контуре l1 в любую точку на контуре l2; R12= [(x2−x1) 2+ (y2−y1) 2+ (z2−z1) 2 ] ½ – расстояние между точками на контуре 1 с координатами х1, у1, z1 и точками на контуре 2 с координатами х2, у2, z2.
– вектор, направленный из произвольной точки на контуре l1 в любую точку на контуре l2; R12= [(x2−x1) 2+ (y2−y1) 2+ (z2−z1) 2 ] ½ – расстояние между точками на контуре 1 с координатами х1, у1, z1 и точками на контуре 2 с координатами х2, у2, z2.
 , т.е. направлен из точки на контуре l2 в точку на контуре l1.
, т.е. направлен из точки на контуре l2 в точку на контуре l1.
 – произвольные векторы.
– произвольные векторы.
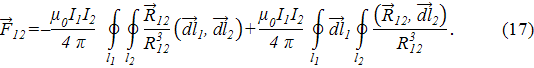



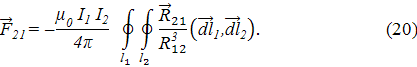
 , то
, то  . Это означает, что в системе двух контуров с постоянными токами соблюдается третий закон (принцип) Ньютона, т.е. действие равно противодействию. Этот же принцип будет соблюдаться и при взаимодействии двух массивных проводников, по которому протекают замкнутые токи, распределенные по объемам проводников V1 и V2 с плотностями
. Это означает, что в системе двух контуров с постоянными токами соблюдается третий закон (принцип) Ньютона, т.е. действие равно противодействию. Этот же принцип будет соблюдаться и при взаимодействии двух массивных проводников, по которому протекают замкнутые токи, распределенные по объемам проводников V1 и V2 с плотностями  . Формула (19) в этом случае принимает вид
. Формула (19) в этом случае принимает вид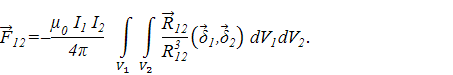
 с заменой
с заменой  .
. с током I2.
с током I2.
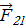 , действующую со стороны элемента
, действующую со стороны элемента 
 на своей оси поля не создает, т.е.
на своей оси поля не создает, т.е.  , и поэтому сила
, и поэтому сила  ; в то же время индукция
; в то же время индукция 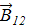 от элемента
от элемента 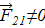 .
.

 .
.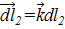 ,
,  ,
,  – орты осей у, z. Тогда
– орты осей у, z. Тогда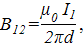

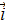 – орт-вектор оси х.
– орт-вектор оси х. , создаваемой вторым током I2 на оси первого, будет направлен по оси у в обратную сторону (рис. 4). С учетом этого выражение для силы
, создаваемой вторым током I2 на оси первого, будет направлен по оси у в обратную сторону (рис. 4). С учетом этого выражение для силы  , действующей со стороны второго провода на первый, примет вид
, действующей со стороны второго провода на первый, примет вид





