
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет механических сил с использованиемСодержание книги
Поиск на нашем сайте
Энергетического метода Методы расчета сил, основанные на применении законов Ампера и Био-Савара-Лапласа, позволяют определять силы, действующие как на каждый отдельный элемент проводника (частичные силы), так на проводник в целом (полные силы). Для расчета полных сил взаимодействия существует и другой метод, основанный на понятии энергии магнитного поля (энергетический метод). Чтобы выяснить физический смысл этого понятия и определить формулы для расчета энергии, рассмотрим систему уравнений, составленную по закону Киргофа для двух неподвижных магнитно–связанных витков:
где е1, е2 – переменные ЭДС, подключенные к каждому витку; r1, r2 – их активные сопротивления; Ψ1, Ψ2 – полные потокосцепления. Умножим уравнение (24) на i1dt, уравнение (25) – на i2dt и сложим их:
Выражение слева есть электрическая энергия dWэл, поступившая в витки от ЭДС за время dt. Первые два слагаемых справа дают потери активной мощности Рdt за то же время. Учитывая, что Ψ1=i1L11+i2L12, Ψ2=i2L22+i1L21, где L11, L22 – собственные, L12=L21 – взаимные индуктивности витков, второй член справа можно представить в виде i1∂Ψ1+i2∂Ψ2=dWм,
где
Индекс L означает, что дифференциал берется при постоянных индуктивностях. Выражение в скобках есть энергия магнитного поля двух магнитно-связанных витков:
В результате баланс энергии приобретает вид
Это соотношение справедливо и для любого числа витков N. В этом случае формула (28) обобщается следующим образом:
Вводя выражение для полного потокосцепления Ψk к -го витка
выражение (30) можно переписать:
Рассмотрим теперь процесс механического взаимодействия двух витков под действием сил магнитного поля. При этом будет использоваться принцип виртуальных перемещений, согласно которому при изменении положения взаимодействующих элементов системы должны меняться только их пространственные (геометрические) параметры. Поэтому токи витков в процессе их движения будем считать постоянными, обозначив их I1 и I2. Каждый элемент dl2 витка 2 испытывает под действием магнитного поля тока I1 витка 1 малое перемещение
Рис. 5. К определению силового действия магнитного поля на виток с током
где dФ12 – магнитный поток, проходящий через поверхность ΔS между контурами l2 и l'2. Если Ф12 – магнитный поток, проходящий через поверхность, опирающуюся на контур l2, Ф'12 – поток через поверхность, опирающуюся на контур l'2 и проходящую через контур l2, то dФ12= Ф'12 – Ф12. С другой стороны, Ф'12= L'12∙I1, Ф12= L12∙I1, где L12, L'12 – взаимные индуктивности между витком 1 и витками 2 и 2' с контурами l2 и l'2 соответственно. Тогда при достаточно малом расстоянии между контурами l2 и l'2 получаем, что dФ12= I1dL12, и в результате согласно (33) работа dA12 будет выражена формулой
где индекс “ I ” означает, что дифференциал берется при постоянных токах. Индуктивность L12 определяется по формуле
Полный дифференциал индуктивности dL12 можно раскрыть следующим образом:
где q1, q2,…,qn – обобщенные координаты (радиус круглого витка, расстояние между витками, угол поворота одного витка относительно другого и т.д.). Частные производные в (36) выражают так называемые обобщенные силы:
Каждая из θk может быть не только силой в обычном смысле, но и, например, моментом вращения, если соответствующая обобщенная координата – угол поворота. Очевидно, что магнитное поле витка действует не только на соседний виток, но и на самого себя. В результате этого воздействия происходит деформация витка, т.е. меняется его форма. Элементарная работа по перемещению
При постоянном токе изменение магнитного потока происходит за счет изменения формы витка, т.е. dФ11=I1dL11, где L11 – собственная индуктивность изменения магнитного потока, определяемая по формуле
Тогда
Очевидно, аналогичное выражение может быть записано и для работы dA22 тока I2 над витком 2:
где L22 – собственная индуктивность витка 2. В результате полное приращение работы магнитного поля в системе двух магнитно-связанных витков dA=dA11+dA12+dA22, или
Выражение (42) получено при условии, что токи при перемещении и деформации остаются постоянными. Однако в процессе движения витков в них согласно закону электромагнитной индукции должны наводиться ЭДС, что приведет к изменению токов. Поэтому, чтобы получить уравнение для энергии магнитного поля, перейдем от постоянных токов к переменным, используя при этом условие квазистационарности, при соблюдении которого взаимодействие между переменными токами в каждый момент времени будет происходить так же, как и между постоянными токами с теми же значениями. Рассмотрим снова систему уравнений для двух магнитно-связанных витков
В уравнениях (43), (44), в отличие от (24), (25), используются полные производные по времени, что подразумевает возникновение ЭДС индукции не только за счет изменения потокосцеплений во времени, но и при движении витков в пространстве. Умножим уравнение (43) на i1dt, а уравнение (44) – на i2dt и сложим их. В результате получим
Так же, как и в (26), выражение слева есть приращение dWэл электрической энергии, поступающей в витки за время dt; первые два члена справа дают потери активной мощности Рdt за то же время. Поскольку уравнения (43), (43) учитывают движение витков, при котором силами магнитного поля совершается определенная работа dA, выражаемая формулой (42), второй член справа следует представить в виде i1dΨ1+i2dΨ2=dWм+dA, откуда
Учитывая, что полные потокосцепления Ψ1=i1L11+i2L12, Ψ2=i2L22+i1L12 (L12=L21), а также формулу (42) для dA, получаем, что
Выражение, от которого берется полный дифференциал, есть мгновенное значение магнитной энергии двух магнитно-связанных контуров с токами, движущихся относительно друг друга:
В результате уравнение энергетического баланса (45) можно переписать в виде
Таким образом, энергия ЭДС тратится на активные потери, механическую работу и на изменение магнитной энергии. Учитывая, что полный дифференциал dWм= (dWм) L+ (dWм) I, согласно формулам (42) и (46) (dWм) I=dA приходим к выводу, что если электромагнитный процесс, описываемый системой (43), (44) на каком-то отрезке времени протекает при неизменных токах, то в таком режиме приращение магнитной энергии равно приращению механической работы (правило джоуль за джоуль). В этом случае для расчета силы взаимодействия двух контуров можно получить удобную расчетную формулу. Если считать витки абсолютно жесткими и перемещающимися по направлению вектора
где q – расстояние между витками (обобщенная координата). Если два абсолютно жестких витка закреплены на одной оси и один из них может вращаться, а другой неподвижен, то, используя в качестве обобщенной координаты угол поворота α, получим формулу для вращающего момента
Выражения (49), (50) справедливы для постоянных токов и остаются справедливыми для переменных токов промышленных частот, на которых соблюдается условие квазистационарности. Однако в этом случае они будут выражать мгновенные выражения сил и моментов, от которых следует перейти к средним за период. Пусть, например, i1=I1мsin (ωt+φ1), i2=I2мsin (ωt+φ2). Тогда после усреднения за период вместо (49), (50) получим выражения
где I1, I2 – действующие значения переменных токов; Отметим, что приведенные формулы справедливы для сил и моментов в системе двух катушек с токами I1, I2 (i1, i2) (рис. 6). При этом в формуле (35) для взаимной индуктивности L12 в качестве l1 и l2 следует использовать полные контуры обмоток катушек, т.е. контуры l1, l2 должны многократно проходить через витки каждой из катушек, образуя w1 и w2 витков соответственно.
Рис. 6. Система двух катушек с токами
В качестве обобщенной координаты q здесь нужно использовать расстояние между осями проводов d. Учитывая, что, согласно (47) магнитная энергия линии на единицу длины
получаем, что сила взаимодействия между проводами линии
Данные формулы согласуются с формулами (23) в разд. 1. Формулы (49) – (52) для расчета сил и моментов показывают, что основой энергетического метода является понятие индуктивности (или взаимоиндуктивности). Поскольку это понятие остается справедливым и для обмоток электрических машин и аппаратов с магнитопроводами из ферромагнитных материалов, энергетический метод можно применять не только для расчета сил в немагнитных средах, но и в неоднородных и, в принципе, даже в нелинейных средах, каковыми и являются по существу ферромагнетики. В качестве первого примера приведем расчет сил, действующих в зазоре модели электромагнита (см. рис. 2). В разд. 1 было показано, что при μ>>1 напряженность поля в зазоре
Тогда потокосцепление
где S – площадь зазора. Индуктивность катушки
Сила F, действующая на поверхность зазора, определяется по формуле
где F0 – сила, действующая на единицу площади зазора, что согласуется с формулой (2) разд. 1. Знак минус означает, что силы магнитного поля стремятся уменьшить зазор (полюсы электромагнита притягиваются друг к другу).
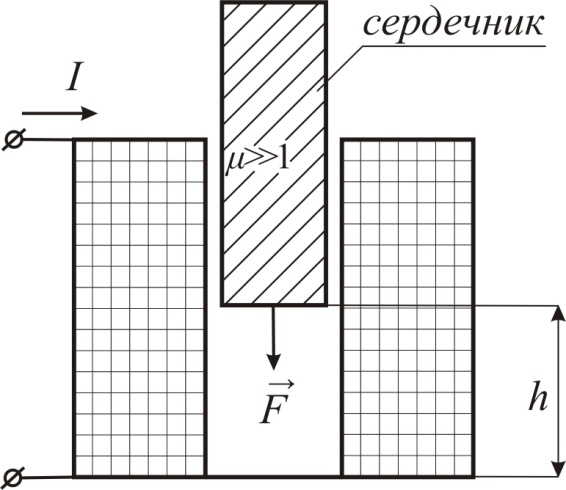
Рис. 7. Катушка с втягивающимся сердечником
устройство применяется в исполнительных механизмах электроавтоматики, реле, а в несколько модифицированном виде – в электроизмерительных приборах электромагнитной системы. Если зависимость индуктивности L катушки от глубины h известна (рассчитана на ЭВМ или получена экспериментально), то сила втягивания
В формулах (53) и (54) I – сила постоянного тока или действующее значение переменного. Необходимость предварительного расчета индуктивности при расчете силовых характеристик реальных электромагнитных устройств ограничивает возможность энергетического метода. Обычно проще оказывается рассчитать поле на ЭВМ, используя специальные численные методы (метод интегральных уравнений или конечных элементов), и затем по известному распределению поля вычислить силы. Кроме того, необходимость детального расчета поля возникает и в тех случаях, когда требуется определить не только полные, но и частичные силы, действующие на каждый элемент конструкции. Если речь идет о расчете распределения сил в немагнитных проводниках, что требуется, например, при проектировании обмоток трансформаторов большой мощности, то такую задачу можно решить с помощью закона Био-Савара-Лапласа (см. разд. 1). В частности, из выражения (5) для объемной плотности FО получается формула
Однако, как было указано в разд. 1, при расчете силовых характеристик электрических машин и трансформаторов основную роль играют силы, действующие на магнитопроводы. Общие расчетные формулы здесь получаются путем использования понятия объемной плотности магнитной энергии wм. Выражение для нее можно получить с помощью формулы (53). Поскольку, согласно этой формуле энергия магнитного поля в зазоре электромагнита
где V=Sh – объем зазора, а напряженность поля в зазоре Н=Iw/h, то объемная плотность энергии в зазоре
что совпадает с выражением (5) для силы, действующей на единицу площади магнетика в однородном поле. С учетом того, что в воздухе B=μ0Н, данное выражение может быть переписано в виде
Эта формула остается справедливой для любого распределения поля в пространстве (а не только для однородного) и для любой магнитной среды, т.е. при B=μ0μН, где μ>>1. Строгий вывод этой формулы производится с использованием уравнений Максвелла.
Понятие плотности энергии магнитного поля позволяет получить путем применения принципа виртуальных перемещений выражения для сил, действующих в объеме и на поверхности магнетиков. Формула для объемной плотности силы имеет вид
Из этой формулы следует, что в однородных магнетиках, т.е. при μ=const, объемные силы, создаваемые полем внешних (по отношению к объему магнетика) источников, отсутствуют. Однако при наличии внешнего поля будут существовать силы, действующие на поверхность магнетика. Если он граничит с воздухом, то поверхностные силы могут быть определены с использованием тензора Максвелла:
где Если проницаемость μ>>1,то
что подтверждает формулу (5). На границе S магнетиков с различными μ cила определяется по следующей формуле, справедливой при любой форме поверхности раздела S:
где Формула (59) получена с использованием тензора Максвелла, с помощью которого объемные силы, действующие на магнетик, сводятся к поверхностным. Как видно из этой формулы, на границе раздела магнитных сред с различными μ возникают силы, действующие как по нормали к поверхности S, так и по касательной. Если в среде 1 проницаемость μ1>>1, в среде 2 μ2=1 (воздух), то Н1=0, Если при конечных μ1, μ2 напряженность магнитного поля в некоторой точке направлена вдоль S, то формула (61) преобразуется к виду
поскольку на границе раздела магнитных сред с различными μ касательные составляющие напряженности равны.
Задание 4.1. Модель электродинамического прибора 4.1.1. При заданных преподавателем постоянных токах катушек I1, I2, числе витков обмоток w1 и w2 и размерах катушек рассчитать на ЭВМ распределение магнитного поля при a= 0, 45°, 90°.Найти области максимальных значений поля при различных a и объяснить полученные результаты. 4.1.2. Рассчитать на ЭВМ при значениях углов поворота подвижной катушки, указанных в пункте 1, величины сил и вращающих моментов. Объяснить полученные результаты. 4.1.3. Рассчитать на ЭВМ зависимости от 4.1.4. Рассчитать вручную зависимость Мвр ( 4.2. Модель электромагнита 4.2.1. При заданных преподавателем размерах и электрических параметрах электромагнита (сила тока I, число витков обмотки w, магнитная проницаемость сердечника и якоря) рассчитать на ЭВМ магнитное поле. Найти на картине поля области максимальных значений напряженности Н и исследовать влияние на эту область изменений магнитной проницаемости сердечника и якоря. Объяснить полученные результаты. 4.2.2. Определить на ЭВМ силу притяжения якоря при различной толщине зазора и различных магнитных проницаемостях сердечника и якоря (задаются преподавателем). 4.2.3. Рассчитать индуктивность в зазоре при тех же значениях толщины зазора, mс и mя по теории магнитных полей и определить соответствующие значения силы по приближенной формуле. Сравнить полученные результаты. 4.3. Катушка со втягивающимся ферромагнитным сердечником 4.3.1. При заданных преподавателем размерах катушки и сердечника, токе I в обмотке, числе витков w и проницаемости сердечника m рассчитать на ЭВМ магнитное поле катушки. Выявить области сгущения поля и определить участки поверхности сердечника, на которых создается основная часть силы, действующей на сердечник. 4.3.2. При заданных преподавателем значениях х1 (3-4 значения), определяющих положение сердечника, рассчитать на ЭВМ силу втягивания сердечника. Объяснить полученные результаты. 4.3.3. Рассчитать на ЭВМ зависимость индуктивности катушки L от величины х1 (8-10 значений). Построить график L (х1). 4.3.4. При тех же значениях х1 рассчитать силу втягивания на ЭВМ по приближенной формуле. Сравнить полученные результаты, объяснить различия.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.31.184 (0.01 с.) |





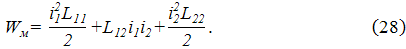




 , величина и направление которого зависят от положения элемента dl2 на контуре l2. В результате перемещения и деформации виток 2 займет положение витка 2 ' с контуром l'2 (рис. 5). Элементарная работа по перемещению каждого отдельного элемента dl2 под действием силы
, величина и направление которого зависят от положения элемента dl2 на контуре l2. В результате перемещения и деформации виток 2 займет положение витка 2 ' с контуром l'2 (рис. 5). Элементарная работа по перемещению каждого отдельного элемента dl2 под действием силы  равна
равна  , где
, где  – индукция, создаваемая током I1 в центре элемента dl2. При этом важно отметить, что данное выражение получено при условии, что виток l1, ток которого I1 создает индукцию
– индукция, создаваемая током I1 в центре элемента dl2. При этом важно отметить, что данное выражение получено при условии, что виток l1, ток которого I1 создает индукцию 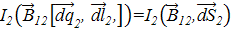 , где
, где  – векторный элемент площади ΔS полоски между контурами l1 и l2 (рис. 5). Суммируя эти величины для всех векторных элементов площади ΔS, для полной работы dA12 по перемещению контура l2 в близкое положение l'2 в пределе получим интеграл
– векторный элемент площади ΔS полоски между контурами l1 и l2 (рис. 5). Суммируя эти величины для всех векторных элементов площади ΔS, для полной работы dA12 по перемещению контура l2 в близкое положение l'2 в пределе получим интеграл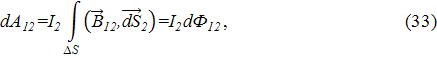


 . (35)
. (35)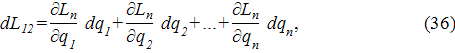

 элемента dl1 витка 1 под действием собственного магнитного поля равна
элемента dl1 витка 1 под действием собственного магнитного поля равна  , где
, где  – индукция, создаваемая током I1, в середине элемента dl1. Полная работа по деформации витка 1 может быть получена путем интегрирования этой элементарной работы по контуру l1. Однако при этом, в отличие от предыдущего варианта двух различных витков, взаимодействие каждой пары элементов
– индукция, создаваемая током I1, в середине элемента dl1. Полная работа по деформации витка 1 может быть получена путем интегрирования этой элементарной работы по контуру l1. Однако при этом, в отличие от предыдущего варианта двух различных витков, взаимодействие каждой пары элементов  и
и  одного и того же витка будет учитываться дважды. Иными словами, при подсчете работы по перемещению элемента
одного и того же витка будет учитываться дважды. Иными словами, при подсчете работы по перемещению элемента 
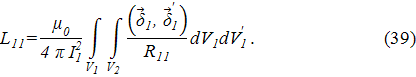









 , то согласно (37) и (47) сила взаимодействия между ними
, то согласно (37) и (47) сила взаимодействия между ними




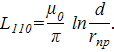


 , где h – толщина зазора.
, где h – толщина зазора.
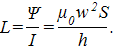


 . (55)
. (55)



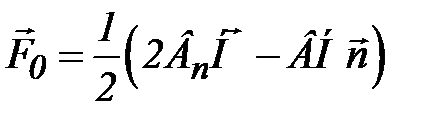 , (59)
, (59)
 – напряженность магнитного поля в воздухе на поверхности магнетика;
– напряженность магнитного поля в воздухе на поверхности магнетика; 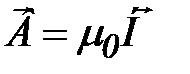 ;
;  , и тогда из (59) следует, что
, и тогда из (59) следует, что
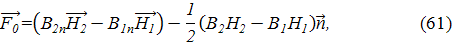
 , и тогда снова получаем формулу (59), т.е. выражение для силы на единицу площади плоской поверхности.
, и тогда снова получаем формулу (59), т.е. выражение для силы на единицу площади плоской поверхности.
 взаимной индуктивности М катушек и момента Мвр при изменении угла
взаимной индуктивности М катушек и момента Мвр при изменении угла 


