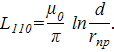Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет сил взаимодействия постоянных токовСодержание книги
Поиск на нашем сайте Основные понятия
Согласно современным физическим представлениям как электрическое, так и магнитное поля следует рассматривать как разновидность материи, которая существует в пространстве независимо от того, пытаемся ли мы ее измерить или нет. Считается, например, что вокруг неподвижного электрического заряда существует электростатическое поле, которое можно обнаружить, внеся в него другой пробный заряд. Наличие поля будет проявляться в движении пробного заряда, т.е. в действии на него некоторой механической силы, создаваемой электростатическим полем.
Аналогичным образом полагается, что вокруг проводника, несущего электрический ток, существует магнитное поле, которое можно обнаружить по движению в этом поле другого проводника с током, возникающего за счет механического взаимодействия этих токов. Таким образом, и электрическое, и магнитное поля являются на самом деле полями сил. Отсюда следует, что в принципе любое из этих полей можно использовать для создания электромеханических устройств. Однако хорошо известно, что в большинстве таких устройств – двигателях, подъемных механизмах, электроизмерительных приборах - чаще всего используется магнитное поле. Чтобы выяснить, почему это происходит, рассмотрим два простейших функционально аналогичных устройства с примерно одинаковым распределением электрического и магнитного полей и сравним их силовые характеристики. Первое из них – плоский воздушный конденсатор, к которому приложено напряжение U (рис. 1,а). Напряжен-
а) б) Рис. 1. Плоский воздушный конденсатор ность поля в плоском конденсаторе
На обкладке конденсатора распределены заряды с поверхностью плотностью σ=e0∙Е. Каждую из обкладок (например, левую) можно рассматривать как заряженную плоскую поверхность, создающую слева и справа от себя напряженность поля
поскольку плотность заряда σ на правой обкладке отрицательна. Такую же силу, но направленную противоположно, будет испытывать и левая обкладка. В результате, поскольку σ=ε0∙Е, для абсолютного значения силы, действующей на единицу площади обкладок, получаем выражение
Воздух пробивается при Е =3∙106 В/м. Поэтому максимально возможное значение силы электрического поля на единицу площади в данном устройстве оказывается не более40 Н/м2. Электрическое поле в плоском конденсаторе (если не учитывать краевых эффектов) можно считать однородным. Примерно такое же магнитное поле возникает и в зазоре ферромагнитного сердечника катушки индуктивности (модель электромагнита), представленной на рис. 2. Чтобы определить его величину, воспользуемся законом полного тока, из которого можно получить следующее соотношение между количеством ампервитков катушки Iw и напряженностями магнитного поля в сердечнике Нс и в зазоре Н (потоками рассеяния пренебрегаем):
где lc – длина средней силовой линии сердечника; d – толщина зазора.
Рис. 2. Ферромагнитный сердечник с воздушным зазором
В зазоре на границе раздела стали и воздуха Н=μНс. Тогда вместо (3) получим
В электротехнической стали сердечника μ>>1, и тогда в зазоре напряженность поля
где Uм – магнитное напряжение. Эта формула по виду совпадает с формулой (1) для напряженности электрического поля в плоском конденсаторе. При этом, поскольку
Справедливость этой формулы подтверждается экспериментально. Кроме того, ее можно получить и теоретическим путем, как частный случай так называемого тензора Максвелла (см. разд. 4). Чтобы сравнить силу электрического поля, действующую на поверхность проводника (обкладки) в конденсаторе (формула (2)), и силу магнитного поля, действующую на поверхность магнетика в зазоре электромагнита, преобразуем формулу (5) к виду
где B=μ0H – индукция магнитного поля. В ферромагнетике, которым является электротехническая сталь, величина индукции не может превышать 2Тn, поэтому максимально допустимая величина силы, действующей на единицу площади поверхности ферромагнетика, примерно равна 8∙105 Н/м2, что на много порядков превышает силу электрического поля (2), действующую на единицу поверхности проводника. Этим и объясняется тот факт, что для силовых электромеханических устройств в основном используется только магнитное поле. При этом, как следует из анализа модели электромагнита, основным элементом такого рода устройств должен быть магнитопровод из ферромагнетика с высокой магнитной проницаемостью и тонким зазором, в котором концентрируется основная часть энергии магнитного поля и возникают электромеханические силы, решающие основную функциональную задачу электромеханического устройства. Таким образом, основной задачей при проектировании силовых электромагнитных устройств является расчет электромагнитного поля при наличии ферромагнетиков. При этом обычно возникает необходимость расчета поля не только на поверхности магнитопроводов, но и в объеме, поскольку они должны работать (в целях достижения максимальных значений индукции) в режимах, близких к насыщению. Задача это довольно сложная и может успешно решаться только с применением численных методов расчета поля и методов конечных элементов и интегральных уравнений, ориентированных на ЭВМ. Однако значительные магнитные силы возникают не только при наличии ферромагнетиков. В обмотках мощных трансформаторов и реакторов, силовых кабелях, энергетических установках (электрооборудование подстанций) токи короткого замыкания могут достигать таких значений, при которых возможны опасные конструктивные деформации и повреждения изоляции. Расчет магнитного поля в этих случаях осложняется быстротой протекающих электромагнитных процессов, что затрудняет применение для расчета сил простых расчетных методик, основанных на законе Ампера. Поэтому расчет электромеханических сил, действующих на токонесущие проводники в режиме переходного процесса, является одной из наиболее актуальных задач современного проектирования электромеханических устройств. Она также должна решаться с применением ЭВМ и использованием современных численных методов. С другой стороны, в настоящее время сохраняют свою актуальность и приближенные инженерные методики расчета сил, развиваемых магнитным полем. Они разделяются на две группы. Первая группа основана на применении законов Био-Савара-Лапласа и Ампера. Она позволяет рассчитывать силы, действующие на токонесущие проводники в немагнитных средах. Эти методы могут применяться и при наличии ферромагнетиков, но при этом нужно каким-либо способом учесть их влияние, например путем введения поверхностных токов или зарядов. Другую группу составляют методы, использующие понятие энергии магнитного поля. Они основаны, как правило, на предварительном расчете индуктивности и взаимной индуктивности. При этом возможен и учет нелинейности ферромагнетиков, которая влияет на величину индуктивности. Вторая группа методов является более универсальной и широко используется при расчете двигателей, электромагнитов, электроизмерительных приборов. И Био-Савара-Лапласа
Известно, что между проводниками, по которым протекают электрические токи, возникают механические силы, зависящие от величины этих токов и взаимного расположения проводников. Согласно современным физическим представлениям, эти силы обусловлены наличием в пространстве, окружающем токи, специфического силового поля, которое существует независимо от того, проявляется ли оно при воздействии на какие-либо другие токи или же в отсутствии таковых не проявляется ни в чем. Это поле сил называется магнитным полем тока, поскольку постоянные магниты создают такие же поля, как и электрические токи. Как показывают опыты, магнитное поле в любой точке пространства может быть охарактеризовано вектором индукции магнитного поля
где вектор
Многочисленные эксперименты по измерению сил, выраженных формулами (7) и (8) показали, что индукция
где магнитная постоянная μ0 =4∙10-7Гн/м; Формула (9) выражает закон Био-Савара-Лапласа. Если подставить в выражение (7) вместо индукции Индукция замкнутого витка с контуром l, по которому протекает ток I, определяется интегралом от выражения (9)
Если магнитное поле создается массивным проводником, по которому протекают постоянные токи с плотностью
Полная сила, действующая на массивный проводник, определяется интегралом по объему от выражения (11)
Когда индукция
Возможность такого обобщения обусловлена тем, что любой массивный проводник с током I можно разделить на совокупность отдельных тонких витков, сумма токов которых равна току I. При этом магнитное поле каждого составляющего тонкого витка может быть определено формулой (10), а сумма этих выражений при достаточно большем их количестве может быть преобразована к интегралу в формуле (13). Пусть теперь на тонкий виток с контуром l2 и током I2 действует магнитное поле витка с контуром l1 и током I1. Тогда сила
Подставляя сюда выражение (10) для
где Аналогичным образом можно получить выражение для силы, действующей со стороны витка 2 с током I2 на виток 1:
где R21=R12; вектор Для упрощения формул (14) и (15) и выяснения их физического смысла воспользуемся известной формулой векторного анализа
где Применяя эту формулу к двойному векторному произведению в (14), получим
Подставляя это соотношение в (14), представим силу
Внутренний интеграл во втором члене справа равен нулю, поскольку подынтегральное выражение является полным дифференциалом:
Поэтому выражение для силы
Тем же способом можно получить и выражение для силы
Поскольку
Такую же форму примет и выражение для силы s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Важно отметить, что принцип действия и противодействия соблюдается только для постоянных токов, которые в силу условия их непрерывности всегда являются замкнутыми. Чтобы это показать, рассмотрим взаимодействие замкнутого витка с контуром l1 и током I1 и незамкнутого элемента Силу
Силу
Первый член справа в (21) равен выражению (22) с противоположным знаком, и поэтому из-за второго члена в (21), в общем случае не равного нулю, принцип действия и противодействия не соблюдается. Он не будет соблюдаться и для двух взаимодействующих незамкнутых элементов, что иллюстрирует рис. 3. Элемент
Рис. 3. Взаимодействие незамкнутых элементов
Простые расчетные формулы для сил можно получить из приведенных выше формул общего вида только для отдельных частных случаев. В качестве простейшего примера приведем расчет сил взаимодействия между прямолинейными параллельными проводами, по которым протекают токи I1, I2 (рис. 4).
Рис. 4. Взаимодействие двух прямолинейных параллельных проводов
Будем считать провода бесконечно длинными. В этом случае индукция магнитного поля не зависит от координаты z, отсчитываемой вдоль проводов. Вектор индукции
Согласно рис. 4,
где d – расстояние между осями проводов. В результате
где Вектор индукции
Таким образом, если I1>0, I2>0, силы, действующие на провода, притягивают их друг к другу. Обычно для длинных проводов рассматриваются силы на единицу длины:
В двухпроводной линии электропередачи I1=I, I2=−I. Тогда
Из этих формул следует, что в двухпроводной линии электропередачи провода отталкиваются друг от друга. В общем случае при произвольных формах проводников расчет сил можно проводить на ЭВМ. При этом каждый контур разбивается на ряд отдельных малых элементов, после чего интегралы по замкнутым контурам заменяются конечными суммами. Расчет сил производится отдельно для каждой проекции вектора силы на оси координат. Аналогичным образом производится расчет сил, действующих на объемные (массивные) проводники. В этом случае объем каждого провода разбивается на совокупность отдельных малых элементов простой формы, в пределах которых плотность тока можно считать постоянной. После этого интегралы по объемам также заменяются конечными суммами. При этом следует отметить, что в случае массивных проводников может возникнуть необходимость предварительного расчета распределения плотности тока по объему проводника. Эта задача может быть решена с использованием теории постоянного электрического поля в проводящей среде путем решения краевой задачи для уравнения Лапласа относительно потенциала плотности тока.
Энергетического метода Методы расчета сил, основанные на применении законов Ампера и Био-Савара-Лапласа, позволяют определять силы, действующие как на каждый отдельный элемент проводника (частичные силы), так на проводник в целом (полные силы). Для расчета полных сил взаимодействия существует и другой метод, основанный на понятии энергии магнитного поля (энергетический метод). Чтобы выяснить физический смысл этого понятия и определить формулы для расчета энергии, рассмотрим систему уравнений, составленную по закону Киргофа для двух неподвижных магнитно–связанных витков:
где е1, е2 – переменные ЭДС, подключенные к каждому витку; r1, r2 – их активные сопротивления; Ψ1, Ψ2 – полные потокосцепления. Умножим уравнение (24) на i1dt, уравнение (25) – на i2dt и сложим их:
Выражение слева есть электрическая энергия dWэл, поступившая в витки от ЭДС за время dt. Первые два слагаемых справа дают потери активной мощности Рdt за то же время. Учитывая, что Ψ1=i1L11+i2L12, Ψ2=i2L22+i1L21, где L11, L22 – собственные, L12=L21 – взаимные индуктивности витков, второй член справа можно представить в виде i1∂Ψ1+i2∂Ψ2=dWм,
где
Индекс L означает, что дифференциал берется при постоянных индуктивностях. Выражение в скобках есть энергия магнитного поля двух магнитно-связанных витков:
В результате баланс энергии приобретает вид
Это соотношение справедливо и для любого числа витков N. В этом случае формула (28) обобщается следующим образом:
Вводя выражение для полного потокосцепления Ψk к -го витка
выражение (30) можно переписать:
Рассмотрим теперь процесс механического взаимодействия двух витков под действием сил магнитного поля. При этом будет использоваться принцип виртуальных перемещений, согласно которому при изменении положения взаимодействующих элементов системы должны меняться только их пространственные (геометрические) параметры. Поэтому токи витков в процессе их движения будем считать постоянными, обозначив их I1 и I2. Каждый элемент dl2 витка 2 испытывает под действием магнитного поля тока I1 витка 1 малое перемещение
Рис. 5. К определению силового действия магнитного поля на виток с током
где dФ12 – магнитный поток, проходящий через поверхность ΔS между контурами l2 и l'2. Если Ф12 – магнитный поток, проходящий через поверхность, опирающуюся на контур l2, Ф'12 – поток через поверхность, опирающуюся на контур l'2 и проходящую через контур l2, то dФ12= Ф'12 – Ф12. С другой стороны, Ф'12= L'12∙I1, Ф12= L12∙I1, где L12, L'12 – взаимные индуктивности между витком 1 и витками 2 и 2' с контурами l2 и l'2 соответственно. Тогда при достаточно малом расстоянии между контурами l2 и l'2 получаем, что dФ12= I1dL12, и в результате согласно (33) работа dA12 будет выражена формулой
где индекс “ I ” означает, что дифференциал берется при постоянных токах. Индуктивность L12 определяется по формуле
Полный дифференциал индуктивности dL12 можно раскрыть следующим образом:
где q1, q2,…,qn – обобщенные координаты (радиус круглого витка, расстояние между витками, угол поворота одного витка относительно другого и т.д.). Частные производные в (36) выражают так называемые обобщенные силы:
Каждая из θk может быть не только силой в обычном смысле, но и, например, моментом вращения, если соответствующая обобщенная координата – угол поворота. Очевидно, что магнитное поле витка действует не только на соседний виток, но и на самого себя. В результате этого воздействия происходит деформация витка, т.е. меняется его форма. Элементарная работа по перемещению
При постоянном токе изменение магнитного потока происходит за счет изменения формы витка, т.е. dФ11=I1dL11, где L11 – собственная индуктивность изменения магнитного потока, определяемая по формуле
Тогда
Очевидно, аналогичное выражение может быть записано и для работы dA22 тока I2 над витком 2:
где L22 – собственная индуктивность витка 2. В результате полное приращение работы магнитного поля в системе двух магнитно-связанных витков dA=dA11+dA12+dA22, или
Выражение (42) получено при условии, что токи при перемещении и деформации остаются постоянными. Однако в процессе движения витков в них согласно закону электромагнитной индукции должны наводиться ЭДС, что приведет к изменению токов. Поэтому, чтобы получить уравнение для энергии магнитного поля, перейдем от постоянных токов к переменным, используя при этом условие квазистационарности, при соблюдении которого взаимодействие между переменными токами в каждый момент времени будет происходить так же, как и между постоянными токами с теми же значениями. Рассмотрим снова систему уравнений для двух магнитно-связанных витков
В уравнениях (43), (44), в отличие от (24), (25), используются полные производные по времени, что подразумевает возникновение ЭДС индукции не только за счет изменения потокосцеплений во времени, но и при движении витков в пространстве. Умножим уравнение (43) на i1dt, а уравнение (44) – на i2dt и сложим их. В результате получим
Так же, как и в (26), выражение слева есть приращение dWэл электрической энергии, поступающей в витки за время dt; первые два члена справа дают потери активной мощности Рdt за то же время. Поскольку уравнения (43), (43) учитывают движение витков, при котором силами магнитного поля совершается определенная работа dA, выражаемая формулой (42), второй член справа следует представить в виде i1dΨ1+i2dΨ2=dWм+dA, откуда
Учитывая, что полные потокосцепления Ψ1=i1L11+i2L12, Ψ2=i2L22+i1L12 (L12=L21), а также формулу (42) для dA, получаем, что
Выражение, от которого берется полный дифференциал, есть мгновенное значение магнитной энергии двух магнитно-связанных контуров с токами, движущихся относительно друг друга:
В результате уравнение энергетического баланса (45) можно переписать в виде
Таким образом, энергия ЭДС тратится на активные потери, механическую работу и на изменение магнитной энергии. Учитывая, что полный дифференциал dWм= (dWм) L+ (dWм) I, согласно формулам (42) и (46) (dWм) I=dA приходим к выводу, что если электромагнитный процесс, описываемый системой (43), (44) на каком-то отрезке времени протекает при неизменных токах, то в таком режиме приращение магнитной энергии равно приращению механической работы (правило джоуль за джоуль). В этом случае для расчета силы взаимодействия двух контуров можно получить удобную расчетную формулу. Если считать витки абсолютно жесткими и перемещающимися по направлению вектора
где q – расстояние между витками (обобщенная координата). Если два абсолютно жестких витка закреплены на одной оси и один из них может вращаться, а другой неподвижен, то, используя в качестве обобщенной координаты угол поворота α, получим формулу для вращающего момента
Выражения (49), (50) справедливы для постоянных токов и остаются справедливыми для переменных токов промышленных частот, на которых соблюдается условие квазистационарности. Однако в этом случае они будут выражать мгновенные выражения сил и моментов, от которых следует перейти к средним за период. Пусть, например, i1=I1мsin (ωt+φ1), i2=I2мsin (ωt+φ2). Тогда после усреднения за период вместо (49), (50) получим выражения
где I1, I2 – действующие значения переменных токов; Отметим, что приведенные формулы справедливы для сил и моментов в системе двух катушек с токами I1, I2 (i1, i2) (рис. 6). При этом в формуле (35) для взаимной индуктивности L12 в качестве l1 и l2 следует использовать полные контуры обмоток катушек, т.е. контуры l1, l2 должны многократно проходить через витки каждой из катушек, образуя w1 и w2 витков соответственно.
Рис. 6. Система двух катушек с токами
В качестве обобщенной координаты q здесь нужно использовать расстояние между осями проводов d. Учитывая, что, согласно (47) магнитная энергия линии на единицу длины
получаем, что сила взаимодействия между проводами линии
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |



 (рис. 1,б). Между двумя разноименно заряженными поверхностями (обкладками) создаваемые ими напряженности поля складываются, а вне обкладок – вычитаются, в результате чего внутри конденсатора напряженность поля
(рис. 1,б). Между двумя разноименно заряженными поверхностями (обкладками) создаваемые ими напряженности поля складываются, а вне обкладок – вычитаются, в результате чего внутри конденсатора напряженность поля 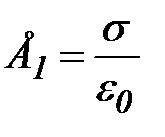 , а снаружи равна нулю. Правая обкладка, находящаяся в поле левой, будет испытывать на единицу площади силу
, а снаружи равна нулю. Правая обкладка, находящаяся в поле левой, будет испытывать на единицу площади силу ,
,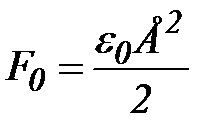 . (2)
. (2)



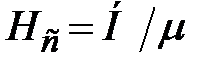 и μ>>1, можно приближенно считать, что в сердечнике напряженность поля равна нулю (идеальный магнетик) и все магнитное поле сосредоточено в зазоре, так же как в конденсаторе электрическое поле сосредоточено между обкладками. Полученная аналогия позволяет рассчитать силы, действующие на полюсы (противоположные плоские поверхности зазора) тем же способом, что и силы, действующие на обкладки конденсатора. Для этого можно условно считать, что на поверхности полюсов распределены магнитные «заряды» с плотностями σм=μ0Н, после чего следует использовать ту же методику, что и при выводе формулы (2). В результате для силы, действующей на единицу площади полюса, получим формулу
и μ>>1, можно приближенно считать, что в сердечнике напряженность поля равна нулю (идеальный магнетик) и все магнитное поле сосредоточено в зазоре, так же как в конденсаторе электрическое поле сосредоточено между обкладками. Полученная аналогия позволяет рассчитать силы, действующие на полюсы (противоположные плоские поверхности зазора) тем же способом, что и силы, действующие на обкладки конденсатора. Для этого можно условно считать, что на поверхности полюсов распределены магнитные «заряды» с плотностями σм=μ0Н, после чего следует использовать ту же методику, что и при выводе формулы (2). В результате для силы, действующей на единицу площади полюса, получим формулу . (5)
. (5)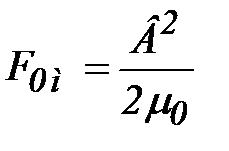 , (6)
, (6) с размерностью В×с/м2 (Т). В частном случае сила
с размерностью В×с/м2 (Т). В частном случае сила  , действующая на элемент dl тонкого провода, по которому протекает ток I, определяется формулой
, действующая на элемент dl тонкого провода, по которому протекает ток I, определяется формулой
 направлен вдоль тока I (т.е. вдоль тонкого провода),
направлен вдоль тока I (т.е. вдоль тонкого провода), 
 , создаваемая элементом тонкого провода dl, по которому протекает постоянный ток I, должна определяться по формуле
, создаваемая элементом тонкого провода dl, по которому протекает постоянный ток I, должна определяться по формуле
 – вектор, направленный из точки расположения элемента dl в точку, где определяется индукция
– вектор, направленный из точки расположения элемента dl в точку, где определяется индукция 
 , меняющейся по объему проводника, то силу, действующую на элемент проводника dV, можно определить по формуле, аналогичной (8):
, меняющейся по объему проводника, то силу, действующую на элемент проводника dV, можно определить по формуле, аналогичной (8):


 , действующая со стороны витка 1 на виток 2, будет выражаться формулой
, действующая со стороны витка 1 на виток 2, будет выражаться формулой
 , получаем
, получаем
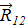 – вектор, направленный из произвольной точки на контуре l1 в любую точку на контуре l2; R12= [(x2−x1) 2+ (y2−y1) 2+ (z2−z1) 2 ] ½ – расстояние между точками на контуре 1 с координатами х1, у1, z1 и точками на контуре 2 с координатами х2, у2, z2.
– вектор, направленный из произвольной точки на контуре l1 в любую точку на контуре l2; R12= [(x2−x1) 2+ (y2−y1) 2+ (z2−z1) 2 ] ½ – расстояние между точками на контуре 1 с координатами х1, у1, z1 и точками на контуре 2 с координатами х2, у2, z2.
 , т.е. направлен из точки на контуре l2 в точку на контуре l1.
, т.е. направлен из точки на контуре l2 в точку на контуре l1.
 – произвольные векторы.
– произвольные векторы.
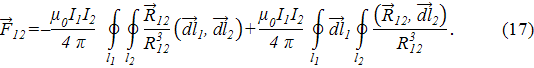



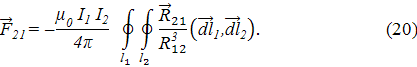
 , то
, то  . Это означает, что в системе двух контуров с постоянными токами соблюдается третий закон (принцип) Ньютона, т.е. действие равно противодействию. Этот же принцип будет соблюдаться и при взаимодействии двух массивных проводников, по которому протекают замкнутые токи, распределенные по объемам проводников V1 и V2 с плотностями
. Это означает, что в системе двух контуров с постоянными токами соблюдается третий закон (принцип) Ньютона, т.е. действие равно противодействию. Этот же принцип будет соблюдаться и при взаимодействии двух массивных проводников, по которому протекают замкнутые токи, распределенные по объемам проводников V1 и V2 с плотностями  . Формула (19) в этом случае принимает вид
. Формула (19) в этом случае принимает вид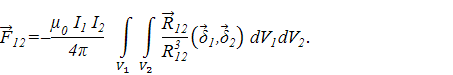
 с заменой
с заменой  .
. с током I2.
с током I2.
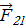 , действующую со стороны элемента
, действующую со стороны элемента 
 на своей оси поля не создает, т.е.
на своей оси поля не создает, т.е.  , и поэтому сила
, и поэтому сила  ; в то же время индукция
; в то же время индукция 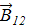 от элемента
от элемента 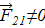 .
.

 .
.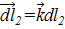 ,
,  ,
,  – орты осей у, z. Тогда
– орты осей у, z. Тогда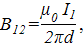

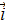 – орт-вектор оси х.
– орт-вектор оси х. , создаваемой вторым током I2 на оси первого, будет направлен по оси у в обратную сторону (рис. 4). С учетом этого выражение для силы
, создаваемой вторым током I2 на оси первого, будет направлен по оси у в обратную сторону (рис. 4). С учетом этого выражение для силы  , действующей со стороны второго провода на первый, примет вид
, действующей со стороны второго провода на первый, примет вид






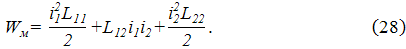




 , величина и направление которого зависят от положения элемента dl2 на контуре l2. В результате перемещения и деформации виток 2 займет положение витка 2 ' с контуром l'2 (рис. 5). Элементарная работа по перемещению каждого отдельного элемента dl2 под действием силы
, величина и направление которого зависят от положения элемента dl2 на контуре l2. В результате перемещения и деформации виток 2 займет положение витка 2 ' с контуром l'2 (рис. 5). Элементарная работа по перемещению каждого отдельного элемента dl2 под действием силы  , где
, где 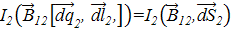 , где
, где  – векторный элемент площади ΔS полоски между контурами l1 и l2 (рис. 5). Суммируя эти величины для всех векторных элементов площади ΔS, для полной работы dA12 по перемещению контура l2 в близкое положение l'2 в пределе получим интеграл
– векторный элемент площади ΔS полоски между контурами l1 и l2 (рис. 5). Суммируя эти величины для всех векторных элементов площади ΔS, для полной работы dA12 по перемещению контура l2 в близкое положение l'2 в пределе получим интеграл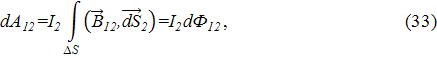


 . (35)
. (35)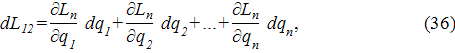

 элемента dl1 витка 1 под действием собственного магнитного поля равна
элемента dl1 витка 1 под действием собственного магнитного поля равна  , где
, где  – индукция, создаваемая током I1, в середине элемента dl1. Полная работа по деформации витка 1 может быть получена путем интегрирования этой элементарной работы по контуру l1. Однако при этом, в отличие от предыдущего варианта двух различных витков, взаимодействие каждой пары элементов
– индукция, создаваемая током I1, в середине элемента dl1. Полная работа по деформации витка 1 может быть получена путем интегрирования этой элементарной работы по контуру l1. Однако при этом, в отличие от предыдущего варианта двух различных витков, взаимодействие каждой пары элементов  и
и  одного и того же витка будет учитываться дважды. Иными словами, при подсчете работы по перемещению элемента
одного и того же витка будет учитываться дважды. Иными словами, при подсчете работы по перемещению элемента 
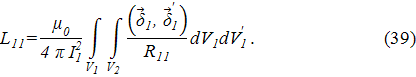






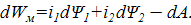



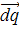 , то согласно (37) и (47) сила взаимодействия между ними
, то согласно (37) и (47) сила взаимодействия между ними