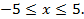Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы, основные операции, определители.Содержание книги
Поиск на нашем сайте
Решить следующие задачи: 13, 16, 21, 47, 64, 69, 261, 276, 795, 800, 802, 809, 839, 843, 863, 866, 869, 882 из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Домашняя самостоятельная работа № 3 Системы линейных уравнений.
Решить следующие задачи: 26, 28, 77, 82, 85, 86, 557, 571, 610, 620, 690, 698, 725 из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Домашняя самостоятельная работа № 4 Векторные пространства.
Решить следующие задачи: 637, 643, 644, 666, 676, 680, 1281, 1311, 1313, 1317, 1321 из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Домашняя самостоятельная работа № 5 Линейные отображения.
Решить следующие задачи: 1441, 1446, 1453, 1467, 1471, 1474 из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Контрольная работа № 1 1. Решить систему уравнений методом Крамера: 2. Решить систему уравнений методом Гаусса: 3. Исследовать совместность, найти общее и одно частное решение системы: 4. Найти собственные числа и собственные вектора матрицы: 5. Найти ранг матрицы в зависимости от параметра 6. Найти базис ядра и базис образа линейного преобразования, заданного матрицей:
7. Линейное преобразование 8. Являются ли линейными преобразования: a) b) c) 9. Найти базис суммы и базис пересечения подпространств
10. Доказать, что собственные векторы, отвечающие различным собственным значениям, линейно независимы. Теоретический опрос № 1
Домашняя самостоятельная работа № 6
Скалярное произведение, ортогонализация. Евклидово пространство.
Решить следующие задачи: 1351, 1354, 1356, 1358, 1360, 1363 из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984; 9, 10, 50, 133, 134, 138, 140, 152, 157, 167, 176, 178, 190, 194, 202 (1, 2) из учебника Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии, М.: Наука, 1976.
Домашняя самостоятельная работа № 7 Кривые в метрическом пространстве. Дифференциальная геометрия поверхностей
1. Определить типы кривых и сделать чертежи: a) c) e) f) 2. Определить типы поверхностей: a) b) c) d) e)
Домашняя самостоятельная работа № 8 Кривые в метрическом пространстве. Дифференциальная геометрия поверхностей. 1. Найти кривизну винтовой линии: 2. Вычислить кривизну и радиус кривизны кривой 3. Найти кривизну и радиус кривизны параболы 4. Найти кривизну эллипса 5. Составить уравнение касательной и нормали к кривой 6. Найти длину дуги параболы 7. Показать, что замкнутая кривая 8. Доказать, что у кривой 9. Составить уравнение поверхности вращения кривой 10. Для поверхности a) Площадь криволинейного треугольника b) Длины сторон этого треугольника; c) Углы этого треугольника. 11. Найти вторую квадратичную форму поверхности вращения
Домашняя самостоятельная работа № 9 Элементы топологии. 1. Являются ли для пространства 2. Пусть 3. Какие из топологий задач 1 и 2 удовлетворяют аксиоме 4. Доказать, что прямая с дискретной топологией удовлетворяет аксиоме 5. Доказать, что все точки Хаусдорфова пространства замкнуты. 6. Что из перечисленного является метрикой для декартова произведения пространств a) b) c) 7. Доказать эквивалентность метрик задачи 6.
Контрольная работа № 2 1. Даны два вектора
2. Доказать тождество 3. Даны две точки A и B, расстояние между которыми равно 2c. Найти геометрической место точек, абсолютная величина разности квадратов расстояний от которых до точек A и B равна 4. Определить тип кривой и сделать чертеж 5. Определить тип поверхности 6. Найти кривизну и радиус кривизны параболы 7. Найти длину дуги параболы Теоретический опрос № 2 1. Дать определение скалярного произведения векторов. 2. Сформулировать неравенство Коши-Буняковского. 3. Описать процесс ортогонализации Грамма – Шмидта. 4. Дать развернутое определение смешанного произведения векторов. 5. Выписать основные виды уравнений кривых второго порядка. 6. Сформулировать основные свойства гиперболы. 7. Сколько существует канонических видов поверхностей второго порядка? 8. Выписать формулу для нахождения длины кривой в метрическом пространстве. 9. Выписать формулу для нахождения радиуса кривизны кривой в метрическом пространстве. 10. Дать определение регулярной поверхности. 11. Сформулировать теорему Бонне. 12. Выписать формулы Гаусса-Петерсона - Кодацци. 13. Дать определение топологического пространства. 14. Сформулировать аксиомы топологии. 15. Дать определение метрики.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.165 (0.01 с.) |

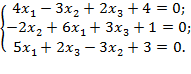
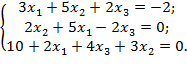
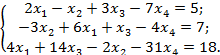
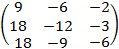 .
. :
: 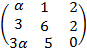 .
.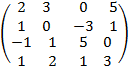 .
.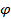 в базисе
в базисе 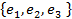 имеет матрицу
имеет матрицу  Найти матрицу этого преобразования в базисе
Найти матрицу этого преобразования в базисе 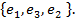


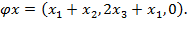
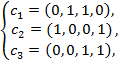 и
и 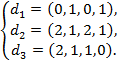
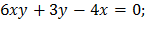 b)
b) 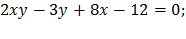
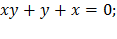 d)
d) 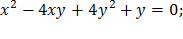
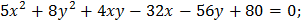
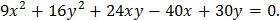
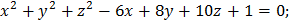
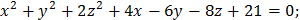

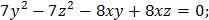
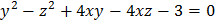 .
.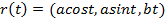 .
.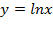 в точке x=1.
в точке x=1.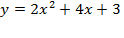 в вершине.
в вершине.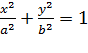 в вершинах.
в вершинах.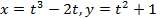 в точке
в точке 
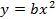 при
при 
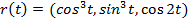 имеет длину 10.
имеет длину 10.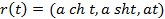 кривизна и кручение равны.
кривизна и кручение равны.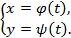 вокруг оси Oz.
вокруг оси Oz.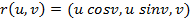 найти:
найти:
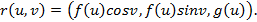
 множества
множества  и
и  топологями на
топологями на 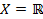 , является ли топологией множество
, является ли топологией множество 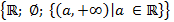 ?
? Колмогорова?
Колмогорова?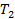 .
.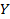 :
: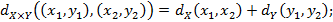
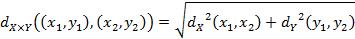 ;
;
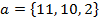 и b
и b 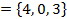 . Найти вектор с длины 1, перпендикулярный векторам a и b и направленный так, чтобы упорядоченная тройка a, b, c имела положительную ориентацию.
. Найти вектор с длины 1, перпендикулярный векторам a и b и направленный так, чтобы упорядоченная тройка a, b, c имела положительную ориентацию.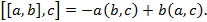
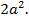

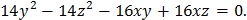
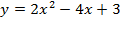 в вершине.
в вершине.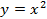 при
при