Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Алгебра и аналитическая геометрия
ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Новосибирск -2011
Учебная программа обсуждена на заседании кафедры ___________________, протокол № ____, от _____
Учебная программа одобрена методическим Советом ВКИ НГУ, протокол №____, от_____.
Программу разработал: к.ф.-м.н., Карпенко А. В.
Рецензенты:
Ответственный за основную образовательную программу: к.ф.-м.н., Амандус Н. Е.
1. Программа учебной дисциплины является частью основной профессиональной образовательной программы прикладного бакалавриата по направлению подготовки
230100. 62 Информатика и вычислительная техника
Профиль подготовки: Информационно-измерительные и управляющие системы
в части освоения основных видов профессиональной деятельности (ВПД):
· проектно-конструкторская деятельность;
· научно-исследовательская деятельность;
и соответствующих профессиональных компетенций (ПК):
· готовить презентации, научно-технические отчеты по результатам выполненной работы, оформлять результаты исследований в виде статей и докладов на научно-технических конференциях (ПК-7);
профессионально-специализированных компетенций (ПСК):
· собирать и анализировать существующие решения аналогичных задач (ПСК 6);
· составлять линейные математические модели элементов систем управления, рассчитывать системы управления при заданных внешних воздействиях, описывать их линейными непрерывными и дискретными моделями (ПСК 17);
· использовать математические модели и методы для анализа, расчетов, оптимизации детерминированных и случайных явлений и процессов (ПСК 18);
общекультурных компетенций (ОК):
· владеет культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения (ОК-1);
· умеет критически оценивать свои достоинства и недостатки, наметить пути и выбрать средства развития достоинств и устранения недостатков (ОК-7);
· использует основные законы естественнонаучных дисциплин в профессиональной деятельности, применяет методы математического анализа и моделирования, теоретического и экспериментального исследования (ОК-10).
2. Место учебной дисциплины в структуре основной профессиональной образовательной программы:
Математический и естественнонаучный цикл, вариативная часть
| Дисциплины, предшествующие по учебному плану
| Требования к первоначальному уровню подготовки обучающихся для успешного освоения дисциплины
| | Уровень «знать»
| Уровень «уметь»
| | Элементы высшей математики
| основы линейной алгебры;
основы теории кривых второго порядка
| · производить основные операции над матрицами,
· считать определители матриц,
· решать СЛУ методом Гаусса,
· решать СЛУ методом Крамера,
· находить обратные матрицы,
· знать основные виды кривых второго порядка
| | Последующие дисциплины учебного плана
|
|
| | Математический анализ
| основы алгебры и геометрии
| · исследовать кривые и поверхности второго порядка,
· находить собственные числа и собственные векторы линейных отображений,
· уметь решать СЛУ
| | ТФКП и основы функционального анализа
| основы алгебры и геометрии
| · производить операции над матрицами,
· уметь решать СЛУ
| 3. Рекомендуемое количество часов/зачетных единиц на освоение примерной программы учебной дисциплины:
максимальной учебной нагрузки студента 108 часов / 3 зачетных единицы, в том числе:
обязательной аудиторной учебной нагрузки обучающегося 54 часов / 1,5 зачетных единицы;
самостоятельной работы обучающегося 54 часов / 1,5 зачетных единицы.
4. Внешние требования
Данный курс является вариативным для математического и естественнонаучного цикла и его содержание соответствует ФГОС ВПО по направлению подготовки «Информатика и вычислительная техника».
Особенности
Примерный перечень особенностей построения учебного курса
И их краткая характеристика
| Особенность (принцип)
| Пояснение
| | Основание для введения курса
| · ФГОС ВПО по направлению подготовки
230100 Информатика и вычислительная техника;
· решение ученого совета ВКИ НГУ.
| | Адресат курса
| Курс адресованстудентам, обучающимся по программе подготовки практико-ориентированного бакалавриата в сокращенные сроки, имеющим среднее профессиональное образование
| | Главная цель курса
| Получить представление:
· об основных видах алгебраических структур;
· о теории векторных пространств;
· об основах аналитической и дифференциальной геометрии;
· об основах топологии;
· о способах решения задач по данным темам.
| | Ядро курса
| Ядро курса составляют следующие темы:
· основные алгебраические структуры;
· векторные пространства и линейные отображения;
· аналитическая и многомерная евклидова геометрия;
· дифференциальная геометрия кривых и поверхностей;
· элементы топологии.
| | Требования к начальной подготовке, необходимые для успешного освоения курса
| Базой для успешного освоениякурсаявляется дисциплина предыдущего уровня образования (СПО) - «Элементы высшей математики», а также хорошая базовая математическая подготовка.
Студент должен «уметь»:
· решать уравнения 3 и 4 степени,
· работать с тригонометрическими функциями и комплексными числами,
· решать тригонометрические уравнения.
|
| Объем в часах курса
| Курс имеет теоретико-ориентированный характертак как соотношение между лекционными и практическими занятиями 2:1.
| | Основные понятия курса
| Группы, кольца, поля; матрицы, СЛУ; векторные пространства, линейные отображения; скалярное, векторное и смешанное произведения; плоские кривые второго порядка, плоскости; кривые в метрическом пространстве, регулярные поверхности; топологические пространства.
| | Обеспечение последующих дисциплин образовательной программы
| Вычислительная математика, математический анализ, ТФКП и основы функционального анализа.
| | Практическая часть курса
| Основные виды работ студента:
· подготовка домашних работ;
· изучение теоретического материала по темам занятий.
| | Области применения полученных знаний и умений
| Знания и умения могут применяться при освоении курсов: вычислительная математика, математический анализ, ТФКП и основы функционального анализа; а также для решения конкретных практических задач, таких как решение СЛУ, исследование кривых и поверхностей и т.п.
| | Описание основных “точек” контроля
| Контроль начального уровня подготовки (беседа);
промежуточный контроль (контрольные работы, самостоятельные работы, домашние задания, опросы по теории);
итоговый контроль (экзамен в устной форме).
|
6. Объем учебной дисциплины, формы и методы организации учебного процесса
| Вид учебной работы
| Объем часов/зачетных единиц
| | Максимальная учебная нагрузка (всего)
| 108
| | Обязательная аудиторная учебная нагрузка (всего)
| 54
| | в том числе:
|
| | практические занятия
| 18
| | контрольные работы
| 4
| | Самостоятельная работа студента (всего)
| 54
| | в том числе:
|
| | выполнение домашних самостоятельных работ
| 50
| | Итоговая аттестация в форме экзамена
|
Цели
| Номер цели по списку
| Уровень освоения
(В результате изучения дисциплины студент будет)
| Описание цели курса
| Обозна-чение компетен-ции
| Компетенция
готовность (активно-действенное состояние) направленное на достижение цели
| | 1.
| ИМЕТЬ ПРЕДСТАВЛЕНИЕ
| о базовых понятиях алгебры, аналитической и дифференциальной геометрии
| ОК 1
| владеет культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения
| | 2.
| о теоретических основах современных алгебры, аналитической и дифференциальной геометрии
| ОК 10
| использует основные законы естественнонаучных дисциплин в профессиональной деятельности, применяет методы математического анализа и моделирования, теоретического и экспериментального исследования
| | 3.
| об основных элементах топологии
| | 4.
| ЗНАТЬ
ЗНАТЬ
| основные виды алгебраических структур
| | 5.
| методы решения СЛУ
| ПСК 18
| использовать математические модели и методы для анализа, расчетов, оптимизации детерминированных и случайных явлений и процессов
| | 6.
| основные понятия теории векторных пространств и линейных отображений
| ОК 10
| использует основные законы естественнонаучных дисциплин в профессиональной деятельности, применяет методы математического анализа и моделирования, теоретического и экспериментального исследования
| | 7.
| основы аналитической и многомерной евклидовой геометрии
| | 8.
| основные виды кривых и поверхностей второго порядка
| | 9.
| основы дифференциальной геометрии кривых и поверхностей
| | 10.
| УМЕТЬ
| ставить задачу и записывать её математическую формулировку
| ПСК 17
ПСК 18
| составлять линейные математические модели элементов систем управления, рассчитывать системы управления при заданных внешних воздействиях, описывать их линейными непрерывными и дискретными моделями
использовать математические модели и методы для анализа, расчетов, оптимизации детерминированных и случайных явлений и процессов
| | 11.
| выбирать наиболее эффективные методы решения
| ПСК 6
| собирать и анализировать существующие решения аналогичных задач
| | 12.
| обосновывать использование выбранных методов
| ПК 6
| обосновывать принимаемые проектные решения, осуществлять постановку и выполнять эксперименты по проверке их корректности и эффективности
| | 13.
| грамотно излагать свои мысли в письменной и устной форме
| ПК 7
| презентации, научно-технические отчеты по результатам выполненной работы, оформлять результаты исследований в виде статей и докладов на научно-технических конференциях
| | 14.
| делать работу над ошибками
| ОК 7
| критически оценивать свои достоинства и недостатки, наметить пути и выбрать средства развития достоинств и устранения недостатков
|
Структура курса
| Алгебра и геометрия
(цели 1-14)
| | Основные алгебраические структуры
(цели 1, 2)
| | Группы, кольца, поля
(цели 1 – 3, 10 – 14)
| | Векторные пространства и линейные отображения
(цели 1, 2)
| | Векторные пространства
(цели 1, 2, 5, 10 – 14)
| | Матрицы, основные операции, определители
(цели 1 – 3, 10 – 14)
| | Системы линейных уравнений (СЛУ)
(цели 1, 2, 4, 6, 10 – 14)
| | Линейные отображения (ЛО)
(цели 1 – 5, 10 – 14)
| | Аналитическая и многомерная евклидова геометрия
(цели 1, 2)
| | Скалярное произведение, ортогонализация. Евклидово пространство
(цели 1, 2, 6, 10 – 14)
| | Поверхности второго порядка
(цели 1, 2,7, 10 – 14)
| | Плоские кривые второго порядка
(цели 1, 2, 7, 10 – 14)
| | Дифференциальная геометрия кривых и поверхностей
(цели 1, 2)
| | Кривые в метрическом пространстве
(цели 1, 2, 9, 10 – 14)
| | Дифференциальная геометрия поверхностей
(цели 1, 2, 9, 10 – 14)
| | Элементы топологии
(цели 1, 2)
| | Топологические пространства
(цели 1, 2, 3, 7 – 14)
|
9. Тематический план и содержание учебной дисциплины
| Наименование разделов и тем
| Содержание учебного материала, практические занятия, самостоятельная работа обучающихся
| Объем часов/зачетных единиц
| Ссылки на цели курса
| |
|
|
| | | Раздел 1.
| Основные алгебраические структуры
|
|
| | Тема 1.1.
Группы, кольца, поля
| Содержание учебного материала
| |
| Общие понятия групп, колец, полей: аксиоматика и примеры. Группы подстановок: разложение в произведение независимых циклов, четные и нечетные подстановки.
|
| 1, 2, 4
| |
| Кольца и поля вычетов по модулю n, кольцо матриц. Подгруппы, подкольца и подполя.
| | Практические занятия
| |
| Задачи на определения группы, кольца и поля.
|
| 4, 10 – 13
| |
| Задачи на тему группа подстановок.
| |
| Задачи на тему кольца вычетов.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 1.
|
| 4, 10 – 14
| | Тема 1.2.
Матрицы, основные операции, определители
| Содержание учебного материала
| |
| Квадратные и прямоугольные матрицы и действия над ними. Трансвекции и диагональные матрицы. Транспонирование матриц.
|
| 1, 2, 4
| |
| Определитель квадратной матрицы. Основные свойства определителей. Миноры и алгебраические дополнения.
| |
| Обратимая матрица. Единственность обратной матрицы и ее вычисление. Формулы Крамера.
| | Практические занятия
|
|
| |
| Задачи на тему действия над матрицами.
|
| 4, 10 – 13
| |
| Задачи на тему определители матриц.
| |
| Задачи на тему обратимость матриц.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 2.
|
| 4, 10 – 14
| | Тема 1.3.
Системы линейных уравнений
(СЛУ)
| Содержание учебного материала
| |
| Запись системы линейных уравнений в матричной форме. Системы линейных уравнений с обратимой матрицей.
|
| 1, 2, 5
| |
| Ранг матрицы. Способы его нахождения. Теорема о ранге.
| |
| Критерий совместности системы линейных уравнений. Эквивалентные системы. Однородная система с квадратной матрицей. Фундаментальная система решений однородной системы. Связь между решениями систем AX=B и AX=0. Общее решение совместной системы.
| | Практические занятия
| |
| Задачи на тему совместность СЛУ.
|
| 5, 10 – 13
| |
| Задачи на тему решения СЛУ методом Гаусса
| |
| Задачи на тему решение СЛУ методом Крамера.
| |
| Задачи на нахождение ранга матрицы.
| |
| Задачи на нахождения фундаментального набора решений однородной системы.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 3.
|
| 5, 10 – 14
| | Раздел 2.
| Векторные пространства и линейные отображения
| | Тема 2.1.
Векторные пространства
| Содержание учебного материала
| |
| Векторное пространство над полем: аксиомы, примеры, линейные комбинации, линейная зависимость, эквивалентные наборы векторов.
|
| 1, 2, 6
| |
| Теорема о замене, ранг набора векторов, равенство рангов эквивалентных наборов.
| |
| База пространства, размерность, координаты, изоморфизм пространств.
| |
| Матрица перехода, ее невырожденность, связь между координатами в разных базах.
| |
| Подпространство, сумма и пересечение подпространств, связь между их размерностями, прямая сумма.
| | Практические занятия
| |
| Задачи на определение и свойства векторных пространств.
|
| 6, 10 – 13
| |
| Задачи на тему база пространства.
| |
| Задачи на нахождение матрицы перехода от одной базы к другой.
| |
| Задачи на нахождение суммы и пересечения подпространств.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 4.
|
| 6, 10 – 14
| | Тема 2.2.
Линейные отображения
(ЛО)
| Содержание учебного материала
| |
| Линейное отображение (ЛО) и его матрица. Координаты образа, связь между матрицами ЛО в разных базах, подобные матрицы.
|
| 1, 2, 6
| |
| Операции над линейными отображениями. Собственные векторы и собственные значения, характеристический полином.
| | Практические занятия
| |
| Задачи на определение линейного отображения.
|
| 6, 10 – 13
| |
| Задачи на связь между матрицами ЛО в разных базах.
| |
| Задачи на нахождение собственных чисел и собственных веторов.
| | Самостоятельная работа студента
| |
| Подготовка к теоретическому опросу № 1.
|
| 1 – 6, 10 –14
| |
| Подготовка к контрольной работе № 1.
| |
| Выполнение домашней самостоятельной работы № 5.
| | Контрольная работа № 1.
|
| 1 – 6, 10 – 14
| | Теоретический опрос № 1.
| | Раздел 3.
| Аналитическая и многомерная евклидова геометрия
| | Тема 3.1.
Скалярное произведение, ортогонализация. Евклидово пространство
| Содержание учебного материала
| |
| Скалярное произведение геометрических векторов и его основные свойства.
|
| 1, 2, 7
| |
| Длина вектора и угол между векторами, неравенство Коши-Буняковского, неравенство треугольника.
| |
| Ортонормированные системы векторов, процесс ортогонализации Грама-Шмидта. Ортогональные разложения пространства.
| |
| Векторное и смешанное произведение векторов, объем параллелепипеда.
| |
| Векторное пространство Rn. Скалярное произведение и ортогональный базис в пространстве Rn.
| |
| Евклидово пространство.
| | Практические занятия
| |
| Задачи на основные свойства скалярного произведения.
|
| 7, 10 – 13
| |
| Задачи связанные с определением длины вектора и угла между векторами.
| |
| Задачи на реализацию процесса ортогонализации Грама-Шмидта.
| |
| Задачи на векторные и смешанные произведения векторов.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 6.
|
| 7, 10 – 14
| | Тема 3.2.
Плоские кривые второго порядка
| Содержание учебного материала
| |
| Плоские кривые второго порядка, их канонические уравнения.
|
| 1, 2, 8
| |
| Эллипс и его свойства.
| |
| Гипербола и её свойства.
| |
| Парабола и её свойства.
| |
| Приведение уравнения кривой к каноническому виду.
| | Практические занятия
| |
| Задачи на основные свойства кривых второго порядка.
|
| 8, 10 – 13
| |
| Задачи на приведение уравнения кривой второго порядка к каноническому виду.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 7 (часть кривые).
|
| 8, 10 – 14
| | Тема 3.3.
Поверхности второго порядка
| Содержание учебного материала
| |
| Канонические уравнения и геометрические свойства поверхностей.
|
| 1, 2, 8
| |
| Приведение к каноническому виду уравнения поверхности.
| | Практические занятия
| |
| Задачи на основные свойства поверхностей.
|
| 8, 10 – 13
| |
| Задачи на приведение уравнения кривой к каноническому виду.
| | Самостоятельна работа студента – выполнение домашней самостоятельной работы № 7 (часть поверхности).
|
| 8, 10 – 14
| | Раздел 4.
| Дифференциальная геометрия кривых и поверхностей
| | Тема 4.1.
Кривые в метрическом пространстве
| Содержание учебного материала
| |
| Обобщенное понятие кривой. Длина кривой в метрическом пространстве.
|
| 1, 2, 9
| |
| Длина участка пути как функция параметра. Стандартные пути (естественно параметризованные кривые).
| |
| Единичный касательный вектор, вектор кривизны и связанные с ним понятия.
| |
| Вычисление единичного касательного вектора и вектора кривизны; формулы Френе.
| | Практические занятия
| |
| Задачи на нахождение длины кривой и длины участка кривой в метрическом пространстве.
|
| 9, 10 – 13
| |
| Задачи на нахождение кривины, вектора кривизны и касательного вектора.
| | Самостоятельная работа студента – выполнение домашней самостоятельной работы № 8 (часть кривые).
|
| 9, 10 – 14
| | Тема 4.2.
Дифференциальная геометрия поверхностей
| Содержание учебного материала
| |
| Регулярные поверхности. Кривизна кривой на поверхности, первая и вторая квадратичные формы..
|
| 1, 2, 9
| |
| Теорема Бонне. Теорема Гаусса и формулы Гаусса-Петерсона-Кодацци.
| | Практические занятия
| |
| Задачи на составление уравнений поверхности вращения.
|
| 9, 10 – 13
| |
| Задачи на нахождение 1 и 2 квадратичных форм и использование формул Гаусса- Петерсона-Кодацци.
| | Самостоятельная работа студента – выполнение домашней самостоятельной работы № 8 (часть кривые).
|
| 9, 10 – 14
|
| Раздел 5.
| Элементы топологии
| | Тема 5.1.
Топологические пространства
| Содержание учебного материала
| |
| Топологическое пространство. Возможность введения различных топологических структур на одном и том же множестве.
|
| 1, 2, 3
| |
| База топологии.
| |
| Аксиомы отделимости.
| |
| Хаусдорфово топологическое пространство.
| |
| Метрическое пространство как топологическое пространство.
| | Практические занятия
| |
| Задачи на определение топологии и её видов.
|
| 3, 10 – 13
| |
| Задачи на определение метрики и эквивалентность метрик.
| | Самостоятельная работа студента
| |
| Подготовка к теоретическому опросу № 2.
|
| 3, 10 – 14
| |
| Подготовка к контрольной работе № 2.
| |
| Выполнение домашней самостоятельной работы № 9
| | Контрольная работа № 2.
|
| 1, 2, 3,7 – 9,
10 – 14
| | Теоретический опрос № 2.
| | Всего:
|
| |
Учебная деятельность
| Ссылка на цели курса
| Темы
| Содержание деятельности
| Формируемые компетенции
| | 1, 2, 4,
10-14
| Группы, кольца, поля
| Изучают основные понятия теории групп; приводят примеры групп, колец и полей; учатся производить операции над подстановками; учатся производить операции в кольце вычетов;
решают задачи.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 4,
10-14
| Матрицы, основные операции, определители
| Повторяют материал, изучавшийся в курсе «Высшая математика»; производят операции в кольце матриц; считают определители; обращают матрицы; анализируют методы нахождения обратных матриц.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 5,
10-14
| Системы линейных уравнений (СЛУ)
| Повторяют материал, изучавшийся в курсе «Высшая математика»; исследуют совместность СЛУ; решают СЛУ методами Крамера и Гаусса; анализируют преимущества и недостатки этих методов; находят фундаментальные наборы решений.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 6,
10-14
| Векторные пространства
| Изучают основы теории векторных пространств; приводят примеры векторных пространств; ищут размерности пространств; находят базы суммы и пересечения подпространств;
находят матрицы перехода от одной базы к другой.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 6,
10-14
| Линейные отображения (ЛО)
| Изучают основы теории линейных отображений; находят координаты образа при ЛО; производят основные операции над ЛО; находят собственные числа и собственные векторы матриц ЛО.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 7,
10-14
| Скалярное произведение, ортоганализация. Евклидово пространство
| Изучают основные понятия; решают задачи на использование основных понятий, в частности находят скалярное, векторное и смешанное произведение; считают объемы параллелепипедов; проводят процесс ортоганазизации.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 7,
10-14
| Плоские кривые второго порядка
| Повторяют материал, изучавшийся в курсе «Высшая математика»; изучают новые факты теории кривых второго порядка; решают задачи на использование свойств кривых второго порядка; приводят кривые второго порядка к каноническому виду; делают эскизы и чертежи.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 8,
10-14
| Поверхности
| Изучают основные виды поверхностей второго порядка и их геометрические свойства; решают задачи на использования свойств; приводят уравнения поверхностей к каноническому виду.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 9,
10-14
| Кривые в метрическом пространстве
| Изучают основные понятия теории кривых в метрическом пространстве; находят длины, длины участков кривых; находят касательные векторы, векторы кривизны, радиусы кривизны; используют формулы Френе.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 9,
10-14
| Дифференциаль-ная геометрия поверхностей
| Изучают основные понятия темы; учатся работать с первыми и вторыми квадратичными формами; используют формулы Гаусса-Петерсона-Кодацци.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
| | 1, 2, 3,
10-14
| Топологические пространства
| Изучают основы топологии; определяю вид топологии; работают с метриками.
| ОК 1, ОК 7, ОК 10, ПК 7, ПСК 6, ПСК 18
|
Требования к минимальному материально-техническому обеспечению
Реализация учебной дисциплины требует наличия учебного кабинета, желательно с мультимедийной техникой.
Требования к экзамену
К экзамену допускаются студенты, успешно справившиеся (получившие оценки не ниже 3) со всеми домашними и контрольными работами.
На экзамене студент должен знать основные понятия курса, уметь доказывать основные теоремы, решать основные (типовые) задачи по темам курса (из самостоятельных работ).
Группы, кольца, поля.
1. Пусть  – множество всех движений плоскости, – множество всех движений плоскости,  - композиция. Является ли - композиция. Является ли
 группой? Если да, то является ли данная группа абелевой? группой? Если да, то является ли данная группа абелевой?
2. Доказать, что нейтральный элемент в группе единственный.
3. Доказать, что обратный элемент в группе единственный.
4. Пусть 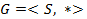 - группа, причем для всякого - группа, причем для всякого  выполнено выполнено  . Доказать, что . Доказать, что  абелева. абелева.
5. Доказать, что пересечение двух подгрупп группы  является подгруппой группы является подгруппой группы  . .
6. Доказать, что числа вида  с рациональными с рациональными  образуют поле. Найти в этом поле число, обратное числу 2 образуют поле. Найти в этом поле число, обратное числу 2 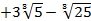 . .
7. Перемножить подстановки:
a)  ; ;
b) 
c) 
8. Найти 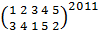 . .
9. Найти декремент 5 8 6 2</m:t></m:r></m:den></m:f></m:e></m:d></m:e><m:sup><m:r><w:rPr><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>-</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
10. Найти все подгруппы группы  . .
11. В  найти обратный элемент к подстановке найти обратный элемент к подстановке 
12. Доказать, что число четных и нечетных подстановок в  одинаково. одинаково.
13. Доказать, что множество всех четных подстановок образует группу относительно операции умножения подстановок.
14. В  найти обратные ко всем элементам. найти обратные ко всем элементам.
15. Найти в  значения значения 
Домашняя самостоятельная работа № 2
Системы линейных уравнений.
Решить следующие задачи:
26, 28, 77, 82, 85, 86, 557, 571, 610, 620, 690, 698, 725
из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Домашняя самостоятельная работа № 4
Векторные пространства.
Решить следующие задачи:
637, 643, 644, 666, 676, 680, 1281, 1311, 1313, 1317, 1321
из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Домашняя самостоятельная работа № 5
Линейные отображения.
Решить следующие задачи:
1441, 1446, 1453, 1467, 1471, 1474
из учебника Проскуряков И.В. Сборник задач по линейной алгебре, М.: Наука, 1984.
Контрольная работа № 1
1. Решить систему уравнений методом Крамера: 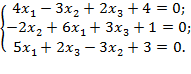
2. Решить систему уравнений методом Гаусса: 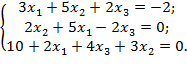
3. Исследовать совместность, найти общее и одно частное решение системы: 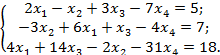
4. Найти собственные числа и собственные вектора матрицы: 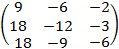 . .
5. Найти ранг матрицы в зависимости от параметра  : : 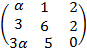 . .
6. Найти базис ядра и базис образа линейного преобразования, заданного матрицей:
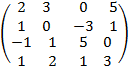 . .
7. Линейное преобразование 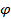 в базисе в базисе 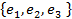 имеет матрицу имеет матрицу  Найти матрицу этого преобразования в базисе Найти матрицу этого преобразования в базисе 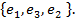
8. Являются ли линейными преобразования:
a) 
b) 
c) 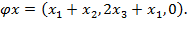
9. Найти базис суммы и базис пересечения подпространств
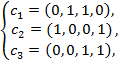 и и 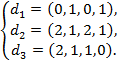
10. Доказать, что собственные векторы, отвечающие различным собственным значениям, линейно независимы.
Теоретический опрос № 1
- Дать определение группы.
- Дать определение подгруппы.
- При каких условиях коммутативное кольцо с единицей является полем?
- Дать определение подстановки.
- Дать определение декремента.
- Сформулировать теорему о разложении подстановки.
- При каких условиях кольцо вычетов является полем?
- Дать определение матрицы.
- Дать определение определителя матрицы.
- Перечислить основные свойства определителей.
- Дать определение ранга матрицы.
- Сформулировать теорему о ранге.
- Сформулировать критерий совместности СЛУ.
- Дать определение векторного пространства над полем.
- Сформулировать теорему о базисе.
- Дать определение линейного отображения.
- Сформулировать теорему-определение невырожденного линейного преобразования.
- Дать определение собственного вектора ЛО.
Домашняя самостоятельная работа № 6
Элементы топологии.
1. Являются ли для пространства 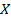 множества множества  и и 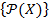 топологями на топологями на 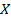 ? ?
2. Пусть 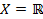 , является ли топологией множество , является ли топологией множество 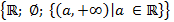 ? ?
3. Какие из топологий задач 1 и 2 удовлетворяют аксиоме  Колмогорова? Колмогорова?
4. Доказать, что прямая с дискретной топологией удовлетворяет аксиоме 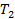 . .
5. Доказать, что все точки Хаусдорфова пространства замкнуты.
6. Что из перечисленного является метрикой для декартова произведения пространств 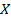 и и 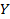 : :
a) 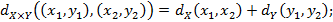
b) 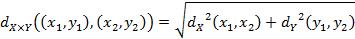 ; ;
c) 
7. Доказать эквивалентность метрик задачи 6.
Контрольная работа № 2
1. Даны два вектора 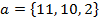 и b и b 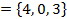 . Найти вектор с длины 1, перпендикулярный векторам a и b и направленный так, чтобы упорядоченная тройка a, b, c имела положительную ориентацию. . Найти вектор с длины 1, перпендикулярный векторам a и b и направленный так, чтобы упорядоченная тройка a, b, c имела положительную ориентацию.
2. Доказать тождество 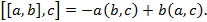
3. Даны две точки A и B, расстояние между которыми равно 2c. Найти геометрической место точек, абсолютная величина разности квадратов расстояний от которых до точек A и B равна 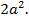
4. Определить тип кривой и сделать чертеж 
5. Определить тип поверхности 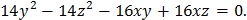
6. Найти кривизну и радиус кривизны параболы 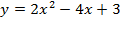 в вершине. в вершине.
7. Найти длину дуги параболы 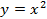 при при 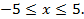
Теоретический опрос № 2
1. Дать определение скалярного произведения векторов.
2. Сформулировать неравенство Коши-Буняковского.
3. Описать процесс ортогонализации Грамма – Шмидта.
4. Дать развернутое определение смешанного произведения векторов.
5. Выписать основные виды уравнений кривых второго порядка.
6. Сформулировать основные свойства гиперболы.
7. Сколько существует канонических видов поверхностей второго порядка?
8. Выписать формулу для нахождения длины кривой в метрическом пространстве.
9. Выписать формулу для нахождения радиуса кривизны кривой в метрическом пространстве.
|



 – множество всех движений плоскости,
– множество всех движений плоскости,  - композиция. Является ли
- композиция. Является ли группой? Если да, то является ли данная группа абелевой?
группой? Если да, то является ли данная группа абелевой?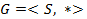 - группа, причем для всякого
- группа, причем для всякого  выполнено
выполнено  . Доказать, что
. Доказать, что  абелева.
абелева. с рациональными
с рациональными  образуют поле. Найти в этом поле число, обратное числу 2
образуют поле. Найти в этом поле число, обратное числу 2 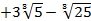 .
. ;
;

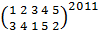 .
.
 .
. найти обратный элемент к подстановке
найти обратный элемент к подстановке 
 одинаково.
одинаково. найти обратные ко всем элементам.
найти обратные ко всем элементам. значения
значения 
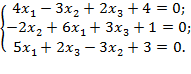
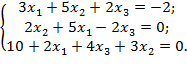
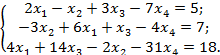
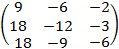 .
. :
: 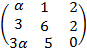 .
.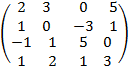 .
.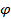 в базисе
в базисе 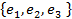 имеет матрицу
имеет матрицу  Найти матрицу этого преобразования в базисе
Найти матрицу этого преобразования в базисе 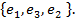


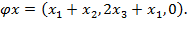
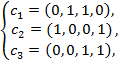 и
и 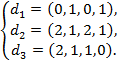
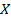 множества
множества  и
и 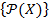 топологями на
топологями на 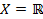 , является ли топологией множество
, является ли топологией множество 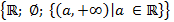 ?
? Колмогорова?
Колмогорова?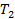 .
.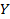 :
: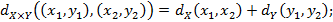
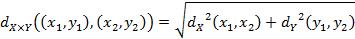 ;
;
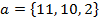 и b
и b 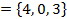 . Найти вектор с длины 1, перпендикулярный векторам a и b и направленный так, чтобы упорядоченная тройка a, b, c имела положительную ориентацию.
. Найти вектор с длины 1, перпендикулярный векторам a и b и направленный так, чтобы упорядоченная тройка a, b, c имела положительную ориентацию.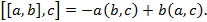
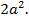

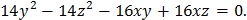
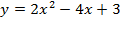 в вершине.
в вершине.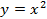 при
при