
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольные материалы (образцы)Содержание книги
Поиск на нашем сайте
Вопросы к экзамену: 1. Общие понятия групп, колец, полей: аксиоматика и примеры. 2. Группы подстановок: разложение в произведение независимых циклов, четные и нечетные подстановки. 3. Кольца и поля вычетов. 4. Основные операции над матрицами, лемма «бухгалтера», кольцо матриц. 5. Матрицы и действия над ними. Трансвекции и диагональные матрицы. Транспонирование матриц. 6. Определитель квадратной матрицы. Основные свойства определителей. Теорема о разложении определителя. Миноры и алгебраические дополнения. 7. Обратимая матрица. Единственность обратной матрицы и ее вычисление. Формулы Крамера. Запись системы линейных уравнений в матричной форме. 8. Системы линейных уравнений с обратимой матрицей. Критерий совместности системы линейных уравнений. 9. Однородная система с квадратной матрицей. Фундаментальная система решений однородной системы. Связь между решениями систем АХ=В и АХ=0. Общее решение совместной системы. 10. Векторное пространство над полем: аксиомы, примеры, линейные комбинации, линейная зависимость, эквивалентные наборы векторов. 11. Теорема о замене, ранг набора векторов, теорема о ранге и её следствие. 12. Базис пространства, теорема о базисе и её следствие. 13. Матрица перехода, ее невырожденность, связь между координатами в разных базах. 14. Подпространство, сумма и пересечение подпространств, связь между их размерностями, прямая сумма. 15. Линейное отображение (ЛО) и его матрица. Координаты образа, связь между матрицами ЛО в разных базах, подобные матрицы. 16. Образ и ядро, ранг и дефект линейного преобразования. Теорема - определение невырожденного линейного преобразования. 17. Собственные числа и собственные векторы линейного преобразования. Линейная независимость собственных векторов, отвечающих различным собственным числам. 18. Скалярное произведение геометрических векторов и его основные свойства. Определение (абстрактного) евклидова векторного пространства, примеры. 19. Векторное пространство 20. Длина вектора и угол между векторами, неравенство Коши-Буняковского, неравенство треугольника. 21. Ортонормированные системы векторов, процесс ортогонализации Грама- Шмидта.
22. Ориентация базиса векторного пространства. 23. Векторное и смешанное произведение векторов, площадь параллелограмма и объем параллелепипеда. 24. Плоские кривые второго порядка, их канонические уравнения и свойства. Приведение уравнения кривой к каноническому виду. 25. Канонические уравнения и геометрические свойства поверхностей. Приведение к каноническому виду уравнения поверхности. 26. Понятие кривой. Длина кривой в метрическом пространстве. Длина участка пути как функция параметра. Стандартные пути (естественно параметризованные кривые). 27. Единичный касательный вектор, вектор кривизны и связанные с ними понятия. Вычисление единичного касательного вектора и вектора кривизны, формулы Френе. 28. Дифференциальная геометрия поверхностей. Регулярные поверхности. Кривизна кривой на поверхности, первая и вторая квадратичные формы. 29. Теорема Бонне. 30. Теорема Гаусса и формулы Гаусса-Петерсона-Кодацци. 31. Топологическое пространство. Возможность введения различных топологических структур на одном и том же множестве. База топологии. 32. Аксиомы отделимости. Хаусдорфово топологическое пространство. Метрическое пространство как топологическое пространство. Классическая и концентрическая топологии на прямой и плоскости.
Варианты самостоятельных и контрольных работ: Домашняя самостоятельная работа № 1 Группы, кольца, поля. 1. Пусть
2. Доказать, что нейтральный элемент в группе единственный. 3. Доказать, что обратный элемент в группе единственный. 4. Пусть 5. Доказать, что пересечение двух подгрупп группы 6. Доказать, что числа вида 7. Перемножить подстановки: a) b) c) 8. Найти 9. Найти декремент 5 8 6 2</m:t></m:r></m:den></m:f></m:e></m:d></m:e><m:sup><m:r><w:rPr><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>-</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
10. Найти все подгруппы группы 11. В 12. Доказать, что число четных и нечетных подстановок в 13. Доказать, что множество всех четных подстановок образует группу относительно операции умножения подстановок. 14. В 15. Найти в
Домашняя самостоятельная работа № 2
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.01 с.) |

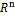 . Скалярное произведение и ортогональный базис в пространстве Rn.
. Скалярное произведение и ортогональный базис в пространстве Rn. – множество всех движений плоскости,
– множество всех движений плоскости,  - композиция. Является ли
- композиция. Является ли группой? Если да, то является ли данная группа абелевой?
группой? Если да, то является ли данная группа абелевой?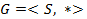 - группа, причем для всякого
- группа, причем для всякого  выполнено
выполнено  . Доказать, что
. Доказать, что  абелева.
абелева. с рациональными
с рациональными  образуют поле. Найти в этом поле число, обратное числу 2
образуют поле. Найти в этом поле число, обратное числу 2 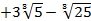 .
. ;
;

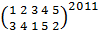 .
.
 .
. найти обратный элемент к подстановке
найти обратный элемент к подстановке 
 одинаково.
одинаково. найти обратные ко всем элементам.
найти обратные ко всем элементам. значения
значения 



