Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кристалографія і мінералогіяСодержание книги Поиск на нашем сайте
Б р и г и н е в и ч Є. А.
. Кристалографія і мінералогія
Лабораторний практикум
2003 Івано-Франківській національний технічний Університет нафти і газу
Кафедра теоретичних основ геології
Бригиневич Є. А.
Кристалографія і мінералогія
Лабораторний практикум
Для студентів спеціальностей „Геологія нафти і газу” та „Геофізичні методи пошуків і розвідки”
М.Івано-Франківськ
МВ 02070855-1149-2003 УДК 551.4.79 Бригиневич Є.А. Кристалографія і мінералогія: Лабораторний практикум. – Івано-Франківськ: Факел, 2003. – 87 с.
Лабораторний практикум розроблений на кафедрі теоретичних основ геології відповідно до навчальної програми з курсу „Кристалографія і мінералогія”. В лабораторному практикумі дається послідовність і короткий зміст лабораторних робіт, приводяться: мета, завдання, основні теоретичні положення та методика виконання, які необхідно засвоїти студенту. Рекомендується література та запитання для самоконтролю.
Рецензенти:
Завідувач кафедри екології ІФНТУНГ, д-р геол.-мінерал. наук, професор Адаменко О.М.
Доцент кафедри екології ІФНТУНГ кандидат геол.-мінерал. наук, Пилипенко А.А.
МВ 02070855-1149-2003 УДК 551.4.79 Бригиневич Є.А. Кристалографія і мінералогія: Лабораторний практикум. – Івано-Франківськ: Факел, 2003. – 90 с. Лабораторний практикум розроблений на кафедрі теоретичних основ геології відповідно до навчальної програми з курсу „Кристалографія і мінералогія”. В лабораторному практикумі дається послідовність і короткий зміст лабораторних робіт, приводяться: мета, завдання, основні теоретичні положення та методика виконання, які необхідно засвоїти студенту. Рекомендується література та запитання для самоконтролю.
Рецензенти:
завідувач кафедри екології ІФНТУНГ, д-р геол.-мінерал. наук, професор Адаменко О.М.
кандидат геол.-мінерал. наук, доцент кафедри екології ІФНТУНГ Пилипенко А.А.
ãДане видання – власність ІФНТУНГ. Забороняється тиражування та розповсюдження
З м і с т
Вступ
Верхня оболонка Землі (земна кора) складається з різноманітних гірських порід і руд, які вміщують або окремі мінерали, або їх асоціації. Вони володіють визначеним хімічним складом, який сформувався внаслідок різноманітних геологічних процесів. Кожному мінералові властивий не тільки свій хімічний склад, але також і внутрішня будова, які разом і визначають їх фізичні властивості. Більшість мінералів в земній корі знаходяться в твердому стані. Серед них виділяють: кристалічні та аморфні. Вони різко відрізняються між собою не тільки внутрішньою будовою, але і зовнішньою формою. Ці особливості багато в чому визначають ті геологічні умови, в яких формувалися окремі мінерали, або їх асоціації. Знання цих особливостей необхідні і при пошуково-розвідувальних, і при експлуатаційних роботах, а також багато в чому визначають не тільки технологію проходки свердловини, але і методику видобутку нафти і газу. Особливе місце при вивченні кристалографії і мінералогії належить лабораторному практикуму, тобто виконанню необхідної кількості лабораторних робіт та домашніх робіт, без яких вивчення програмного матеріалу курсу практично неможливе. Перша частина учбового посібника включає основні лабораторні роботи з геометричної кристалографії мінералів і їх морфологічним особливостям (які сформувалися при різноманітних геологічних процесах як в надрах Землі, так і на її поверхні). Друга частина присвячена вивченню діагностичних ознак мінералів та їх місця в класифікації. Кожна лабораторна робота включає: мету, завдання, послідовність її виконання, основні теоретичні положення, методичні рекомендації, питання самоконтролю, висновки та перелік літературних джерел, необхідних для виконання роботи. Враховуючи те, що останніми роками зростає роль самостійного засвоєння студентами матеріалу, кожну лабораторну роботу рекомендується виконувати в декілька етапів. На першому етапі студент знайомиться з цільовим положенням, як за посібником, так і за рекомендованою літературою. Сутність другого етапу полягає в контролі самостійно засвоєного матеріалу. Третій етап – основний. Він виконується безпосередньо в лабораторії під керівництвом викладача згідно поставленого завдання з окремих питань. При цьому студент на початку знайомиться з основними засобами виконання визначених операцій, а потім приступає до реалізації поставлених завдань. Четвертий етап – підсумковий і полягає в тому, що кожний студент за результатами теоретичного засвоєння програмного матеріалу та лабораторних досліджень повинен зробити основні висновки, положення яких він і буде захищати при поданні звіту з лабораторної роботи. За результатами захисту звіту лабораторної роботи студент отримує відповідний бал. Об’єм годин, який необхідний на виконання кожної окремої лабораторної роботи визначається учбовим планом кожної спеціальності та залежить від специфіки профілю спеціаліста, якого готують. В основу даного лабораторного практикуму покладені матеріали ведучих українських, закордонних та радянських вчених, з робіт яких використані не тільки окремі визначення, висновки і методичні рекомендації, але й ряд ілюстрацій. Серед них особливе місце відведено підручникам по кристалографії і морфології мінералів У.Г.Попова та І.І.Шафрановського, М.П.Шаскольскої, Е.Е.Флінта, Г.Ф.Вульфа, Є.Лазаренко, І.Костова та інші.
Зміст лабораторних робіт
Лабораторна робота № 1 Симетрія кристалів та їх визначення
Мета: засвоїти основні закони кристалографії для визначення симетрії кристалів та їх місця в класифікації симетрії. Завдання:
1 Вивчити основні закони кристалографії; 2 Опанувати основні методи визначення симетрії кристалів та теорем виводу 32 видів симетрії; 3 Згідно з варіантом № визначити основні кристалографічні параметри моделей кристалів і встановити їх місце в класифікації симетрії.
Рисунок 1.5 - Взаємозв’язок між: а - елементами огранювання кристалу (вершини, ребра, грані) і б - елементи просторової гратки (вузли, просторові ряди, плоскі сітки).
Ребра в ідеальному вигляді являють собою прямі лінії, які утворюються на перетині двох граней і на мікрорівні відповідають просторовим рядам просторових граток (рис. 1.5, а). Кількість ребер та їх величина знаходяться у прямій залежності від внутрішньої будови кристалу. Вершини – місце перетину ребер кристалу. Вони відповідають просторовим вузлам (рис. 1.5, б). Між гранями, ребрами та вершинами існує певна кількісна взаємозалежність, відома під назвою закону Ейлера-Декарта, що має такий вираз [2]
∑граней + ∑вершин = ∑ребер + 2 При вивченні елементів огранення кристалів, а саме реальних, рекомендується подумки доповнити відсутні або продовжити слабо розвинені грані або ребра, провести їх підрахунок і встановити між ними відповідний зв’язок згідно з законом Ейлера-Декарта [4]. У зв’язку з тим, що плоскі сітки просторової гратки розміщені одна відносно одної під певними кутами, грані кристалів, які відповідають цим сіткам також знаходяться під такими ж кутами. На цій фундаментальній властивості кристалічної речовини базується закон постійності двогранних кутів: ”При постійних фізико-хімічних умовах (температура, тиск, концентрація) кути між однотипними парами граней даної кристалічної речовини завжди постійні”. 1.3 згідно з Є.С.Федоровим „Симетрія є властивість геометричних фігур в різних положеннях приходити в суміщення з первинним положенням, відповідно, ця закономірна повторюваність – для однакових граней, ребер і кутів” [1]. Таким чином, симетрією називається властивість геометричних фігур повторювати свої аналогічні частини певне ціле число разів. Основні операції, за допомогою яких визначається симетрія кристалів, такі: - відбиття аналогічних частин кристалу через його центр (з подальшим поворотом) – центр інверсії; - суміщення окремих частин кристалу з аналогічним поворотом його навколо прямої – вісі симетрії; - суміщення - відбиття часини кристалу через його центр с подальшим поворотом навколо вибраної вісі цієї частини на певний кут - через вісь інверсії; - суміщення - відбиття частини кристалу через дзеркальну площину - площину симетрії. В комплекс елементів симетрії входить: центр інверсії - C; поворотні вісі симетрії – L; інверсійні вісі симетрії – Li; площини симетрії – P; одиничні напрями – OH. Центром інверсії називається така точка в середині фігури, через яку, як що провести пряму, то по обидві сторони від неї на однакових відстанях знаходяться аналогічні частини фігури. Як бачимо на рис. 1.6, проведені прямі АА1, ВВ1, ДД1 на однакових відстанях від точки С по обидві сторони мають аналогічні частини трикутників А В Д і А1В1Д1.
а б
Рисунок 1.6 – (а) - ілюстрація оберненої (інверсійної) паралельності двох трикутників пов’язаних центром інверсії, (б) – два паралелограми, грані яких пов’язані між собою центром інверсії
Для визначення центру інверсії в моделях рекомендується: покласти їх на рівну площину (стіл, дошка), а паралельність відповідної їй верхньої грані, визначити лінійкою. Якщо кожна грань має собі паралельну – центр інверсії присутній. При визначенні центру інверсії в кристалах необхідно пам’ятати одну з теорем (теорема 1), яка говорить, що „При наявності в кристалі осі симетрії парного порядку і площини симетрії, розміщеної перпендикулярно до цієї осі, центр інверсії присутній” [6]. Поворотною віссю симетрії (L) називається пряма, при повороті навколо якої на 3600 частини фігури повторюються „n” ціле число разів. Для того, щоб дати характеристику осі симетрії, необхідно знайти найменший кут обертання, який веде до само суміщення аналогічних частин фігури. Такий кут називається елементарним кутом обертання – a. Відповідно порядок осі симетрії відповідає числу, яке показує, скільки разів елементарний кут a повторюється при обертанні кристалу навколо осі симетрії на 3600. У кристалічних багатогранниках існують поворотні осі симетрії другого (L2, a=1800), третього (L3, a=1200), четвертого (L4, a=900), шостого (L6, a=600), порядків (рис. 1.7). Осі першого порядку (L1, a=3600) присутні в усіх кристалах в необмеженій кількості.
Поворотні осі симетрії діляться на полярні - ті, що перетинають різні елементи огранювання кристалу (грань - вершина; див. рис. 1.7в), і біполярні - ті, що проходять через однакові елементи огранювання (грань - грань; рис.1.7а,б,г), ребро - ребро, вершина - вершина). При визначенні осей симетрії необхідно пам’ятати, що їх кількість і порядок визначається двома теоремами [1]: Теорема 2. При наявності центру інверсії та площини симетрії перпендикулярно до останньої розміщується вісь симетрії парного порядку. Теорема 3. При наявності центру інверсії та осі симетрії парного порядку Ln (L2, L4, L6) перпендикулярно до останньої розміщуються „n” - число осей другого порядку. Інверсійною віссю симетрії називається пряма, при повороті навколо якої на 3600 з відповідним переносом - відбиттям (інверсією) через центр кристалу аналогічні частини суміщаються самі із собою „n” ціле число разів. В кристалах можуть бути присутні інверсійні осі четвертого Li4 (рис. 1.8, а) і шостого Li 6 (рис. 1.8, б) порядків.
а) – Li 4 (інверсія грані АВС з поворотом на 900 в грань СДВ); б) – Li 6 (інверсія грані АВС з поворотом на 600 в грань ДАЕ).
Рисунок 1.9 - Площини симетрії в багатогранниках: а) прямокутний паралелепіпед має три площини симетрії – дві вертикальні (P1 і P2) і одну горизонтальну (P3); б) – куб має дев’ять площин симетрії – чотири вертикальних (P1, P2, P3, P4), чотири похилі (P5, P6, P7, P8) і одну горизонтальну (P9). Відносно елементів огранювання кристалів (грані, ребра, вершини) площини симетрії можуть проходити через ребра (вздовж і впоперек), перпендикулярно до граней і через вершини, поділяючи гранні кути на дві рівні частини. Кількість площин симетрії і порядок їх розміщення в кристалі визначається двома теоремами [4,5]: Теорема 4. При наявності центру інверсії і осі симетрії парного порядку перпендикулярно до останньої розміщується площина симетрії. Теорема 5. При наявності осі симетрії і хоча б однієї площини симетрії, яка проходить вздовж цієї осі, відповідно маємо „n” площин, які проходять вздовж цієї ж осі. 1.4 Одиничним напрямом (ОН) називається напрям (пряма) в кристалах, який не має собі аналогічного, тобто не повторюється. В кристалах може бути присутнім один одиничний напрям (рис. 1.10, а), три (рис.1.10, б), багато (рис.1.10, в), необмежена кількість (рис.1.10, г).
У відношенні розміщення одиничних напрямів щодо елементів симетрії, то вони можуть проходити через центр інверсії, співпадати з площинами та осями симетрії або розміщатися перпендикулярно до них. Крім одиничних напрямів у кристалах присутні так звані симетрично-рівні напрями, тобто такі, які повторюються декілька разів. Вони розміщені похило до L2, L3, L4, L6, P або співпадають з 3L2, 4L2, 6L2, 4L3, 3L4. Якщо напрям має собі аналогічний, тобто є його дзеркальним відбиттям відносно площини симетрії, або як такий, що повторюється відносно будь-якої вісі симетрії „n” разів, то такий напрям є симетрично-рівним. Вчення про елементи симетрії та одиничні напрями дозволили зробити математичну класифікацію всіх кристалічних тіл і згрупувати їх у певні класифікаційні одиниці - види (класи) симетрії, сингонії та категорії (табл. 1.1, 1.2) 1.5 Вивід видів симетрії з одиничними напрямами. До одиничного напряму ОН, який в подальшому іменується вихідним, поступово приєднуються:
1.6 Вивід видів симетрії без одиничних напрямів. Враховуючи, що в даних кристалічних багатогранниках одиничні напрями відсутні, за вихідні беруться осі симетрії трьох основних фігур кубічної сингонії: тетраедра, гексаедра, октаедра. Отже: § сукупність осей симетрії тетраедра (4L3,3L2) береться за примітивний вид (табл. 1.1); § для виводу центрального виду додається С. Згідно з теоремою 1, перпендикулярно до кожної L2 будуть P. Формула буде 4L3,3L23PC; § для виводу планального виду симетрії вздовж 4L3 проводять площини симетрії P. Згідно з теоремою 5 вздовж кожної L3 проводяться 3P, причому кожна Р проходить одночасно і через 2L2. Отже кінцева формула симетрії буде 4L3,3Lі6Р(4L33Lі46L2); § для виведення аксіального виду симетрії до 4L3 перпендикулярно додаємо L2, в підсумку одержавши 3L44L36L2. § приєднуючи до виведеного виду симетрії 3L44L36L2 центр інверсії С, враховуючи теорему 4, одержимо планаксіальний вид симетрії 4L33L46L29Р.
Таблиця 1.1 - Класифікація і формули симетрії кристалічних
Таблиця 1.2 - Характеристика сингоній і категорій кристалів
1.7 Російський вчений А.В.Гадолін довів, що в кристалах можливі 32 різні комбінації елементів симетрії, що називаються видами, чи класами симетрії. Всі види симетрії групуються за ступенем складності в сім великих груп, чи систем – кристалографічних сингоній (табл. 1.3). Серед них виділяють нижчі, середні, вищі. Найменш симетричні - кристали триклинної сингонії. В них серед усіх можливих елементів симетрії часто спостерігається лише центр симетрії, але іноді він відсутній. Цей вид сингонії характерний для альбіту, мікрокліну та іншім мінералам. Таблиця 1.3 - Характеристика сингоній багатогранників
До моноклінної сингонії відносяться кристали, які мають або одну площину симетрії, або одну вісь другого порядку, або і ту і другу разом із центром інверсії. До цієї категорії належать ортоклаз, гіпс, мусковіт, деякі амфіболи. Ромбічна сингонія характерна для кристалів з одною або трьома осями другого порядку і двома або трьома площинами симетрії (L22P або 3L23PC), а також кристали з трьома осями другого порядку (3L2) без площини симетрії. В поперечному розрізі вони мають форму ромба. Перераховані види симетрії належать до категорії нижчих сингоній. До середніх сингоній належать кристали лише з одною віссю симетрії вищого порядку, це кристали гексагональної і тетрагональної сингоній, форми яких дуже подібні. В тригональній сингонії вище поєднання елементів симетрії - L33L23PC. Типова форма кристалів даної сингонії, наприклад, кристалів кальциту, доломіту, магнезиту, гематиту - ромбоедри. До цієї ж сингонії належать корунд і кварц, хоча кристали останнього мають вигляд гексагональних призм, увінчаних мовби гексагональними пірамідами. В дійсності вершини кварцу являють собою комбінацію двох ромбоедрів. Тетрагональна, чи квадратна сингонія відрізняється присутністю в кристалах однієї осі четвертого порядку. В розрізі, перпендикулярному до цієї осі, зазвичай спостерігається форма квадрата, чи восьмикутника. Вищим поєднанням елементів симетрії в даній сингонії може бути L44L25PC. Ця сингонія характерна, наприклад, халькопіриту і рутилу. Для кристалів гексагональної сингонії характерна форма шестигранних призм, грані яких - паралельні осі шостого порядку L6. Такими є кристали апатиту і берилу. Вище поєднання елементів симетрії – L66L27PC. До вищої сингонії належать кубічна, яка об’єднує найбільш симетричні кристали (кам’яна сіль, пірит, алмаз, магнетит). Вони мають вигляд кубів, октаедрів та інших. Вище поєднання елементів в кубічній сингонії 3L44L36L29PC. Таким чином, при визначенні симетрії реальних кристалів, необхідно брати до уваги цілий ряд ознак. Симетрії підкоряються також і фізичні властивості кристалів (електричні оптичні, механічні і інші.). Тому, встановлюючи істинну симетрію кристалічних багатокутників, потрібно враховувати їх фізичні властивості. Сукупність даних, одержаних всіма вказаними методами, дозволяє встановити симетрію реальних кристалів[3] Вивченням кристалічних форм і структур мінералів займаються науки кристалографія [2] і мінералогія [3, 4], що буде розглянуто в наступних лабораторних роботах.
Короткі рекомендації Таблиця 1.4 - Визначення симетрії кристалів
Звіт з лабораторної роботи 3.1 Оформлюється кожним студентом індивідуально за загальними вимогами. 3.2 Звіт повинен містити: мету, завдання, основні теоретичні положення про головні особливості кристалів, їх елементів огранювання та внутрішньої будови, що визначає їх симетрію (особливу увагу необхідно звернути: на основні виводи 32 видів симетрії, основні закони кристалічних багатогранників, основні способи класифікації їх за симетрією), порядок виконання лабораторної роботи, результати власних досліджень згідно з отриманим варіантом, висновки та перелік літературних джерел, який був використаний при виконанні даної роботи. 3.3 Звіт захищається кожним студентом за системою контрольних питань. Питання для самоперевірки 1 Назвіть головні елементи симетрії кристалів? 2 Що є кристал? 3 Чи пов’язані між собою одиничні напрямки та вісі симетрії в кристалах? 4 Що таке вісь симетрії? 5 Що таке площина симетрії? 6 Що таке центр інверсії? 7 Які лінійні параметри кристалічної гратки кристалів Ви знаєте? 8 Назвіть один з основних законів кристалографії? 9 На основі яких теорем визначається симетрія кристалів? 10 Що є сингонія? 11 Що є категорія? 12 Які основні принципи закладені в класифікацію симетрії кристалів? 13 Що таке одиничний напрямок в кристалах? 14 Як можуть розміщуватися одиничні напрямки по відношенню до елементів симетрії?
Література 1. Куровець М. Кристалографія і мінералогія. Ч.I. Кристалографія мінералів.– Л.: Світ, 1996. – 236 с. 2. Шаскольська М. Кристаллографія.-М.: „Высшая школа”, 1976. 3. Павлинов В. и др. Пособие к лабораторным занятиям по общей геологии. Учеб. Пособие для ВУЗов.-4-е изд., перераб. и доп.-М.: Недра, 1988.-149 с. 4. Попов Г., Шафроновский И. Кристаллография. Изд. 5-е. Учебник для студентов геологических специальностей высших учебных заведений. М.: „Высшая школа”, 1972.
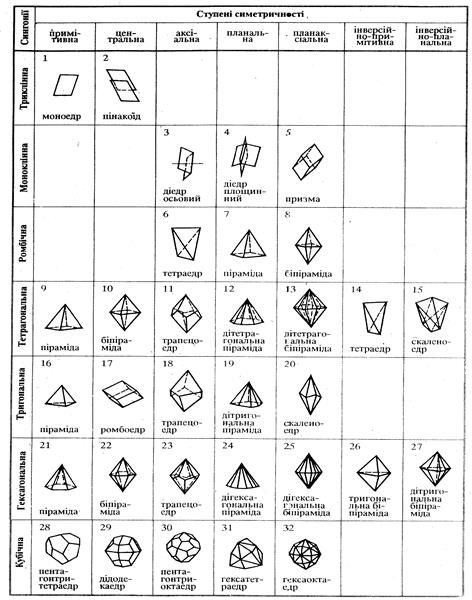
Лабораторна робота № 2 А б в Рисунок 2.1 - Приклад простих форм: а – відкрита, складена трьома прямокутними гранями; б – закрита, складена чотирма трикутними гранями; в – закрита, складена шістьома квадратними гранями. Проста форма, грані якої розміщуються похило відносно всіх осей і площин симетрії, називається загальною. Проста форма, грані якої розміщуються перпендикулярно або паралельно відносно хоча б однієї осі і площини симетрії або рівно похилі до двох однакових елементів симетрії носить назву конкретної. Для деяких простих форм, які характеризуються наявністю поворотних осей симетрії L2, L3, L4, L6 властиві явища енантіоморфізму, тобто наявності правих і лівих форм. Для цих простих форм характерно зміщення – закручення граней в праву і ліву сторони. 1.2 Вчення про прості форми кристалів і їх видів [1] дозволили встановити серед них найбільш характерні, які одержали назву характеристичних (табл. 2.1). Так, в трикліній сингонії виділено дві характеристичні прості форми (моноедр і пінакоїд), в моноклінній – три (дієдр осьовий, дієдр площинний і призма), в ромбічній – три (тетраедр, піраміда і біпіраміда), в тригональній – п’ять (піраміда, ромбоедр, трапецоедр, дітригональна піраміда і скаленоедр), в тетрагональній – сім (піраміда, біпіраміда, трапецоедр, дітетрагональна піраміда, де тетрагональна біпіраміда, тетраедр, скаленоедр), в гексагональній – сім (піраміда, біпіраміда, дігексагональна піраміда, дігексагональна біпіраміда і тригональна біпіраміда), в кубічній - п’ять (пентагонтритетраедр, дідодекаедр, пентагонтриоктаедр, гексатетраедр, гексаоктаедр). Таблиця 2.1 - Характеристичні прості форми 32 видів симетрії
Як видно, до характерних простих форм належать прості форми з максимальним розвитком граней в кожній із семи ступенів симетричності (табл. 2.2, 1.3) [2]. Таблиця 2.2 - Назва 32 видів (класів) симетрії кристалів згідно характеристичних простих форм
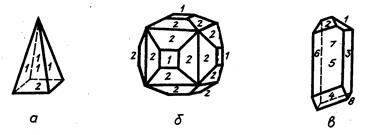
Визначення простих форм кристалів рекомендується проводити таким чином: а) суміщенням вихідної грані простої форми з аналогічною обертом її на певний кут навколо поворотної осі симетрії; б) відбиттям вихідної грані простої форми з аналогічною через площину симетрії; в) відбиттям – інверсією вихідної грані простої форми з аналогічною через центр інверсії; г) суміщенням – інверсією вихідної грані простої форми з аналогічною поворотом навколо осі інверсій і наступним відбиттям через центр. При визначенні простої форми на відповідних моделях необхідно пам’ятати, що вони подані в ідеальному вигляді, тобто відповідають математичній моделі кристалу. На реальних кристалах в більшості випадків зовнішня форма простих форм і їх відносні розміри не відповідають ідеальним моделям. В цих випадках при визначенні простих форм візуальним методом необхідно особливу увагу звернути на взаємо розміщення окремих граней і уявно пов’язати їх так, щоб в кінцевому підсумку уявити кристал в ідеальному вигляді. 1.3 Комбінація являє собою сукупність простих форм, пов’язаних між собою комплексом елементів симетрії (за винятком комбінацій примітивного виду триклинної сингонії, в якому елементи симетрії відсутні). Серед комбінацій виділяють: прості, які складаються з одного виду простих форм, і складні, що складені різними простими формами (рис. 2.2).
Рисунок. 2.2 - Приклади комбінацій: а - комбінація тетрагональної піраміди (1) і моноедра (2); б – комбінація куба (1) і тетрагексаедра (2); в – комбінація 8 – моноедрів (1, 2, 3, 4, 5, 6, 7, 8).
Кількість простих форм, що входять в цю чи іншу комбінацію, виводиться математично графічним шляхом і визнача
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.016 с.) |

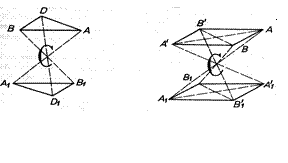
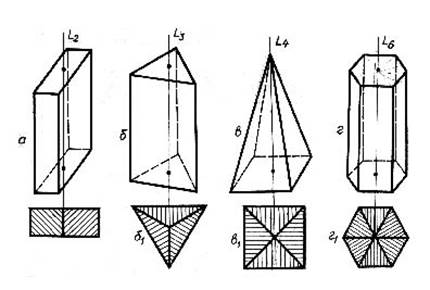 Рисунок 1.7- Приклади багатогранників з поворотними осями симетрії а–а1 – L2; б–б1 – L3; в–в1 – L4; г–г1 – L6
Рисунок 1.7- Приклади багатогранників з поворотними осями симетрії а–а1 – L2; б–б1 – L3; в–в1 – L4; г–г1 – L6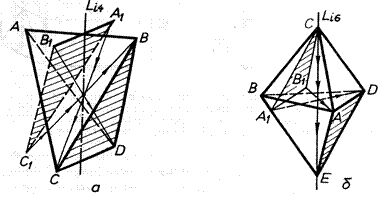 Рисунок 1.8 - Приклади багатогранників з інверсійними осями:
Рисунок 1.8 - Приклади багатогранників з інверсійними осями: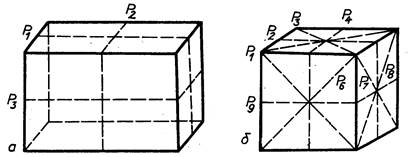 Площина симетрії – це площина, яка ділить кристал на дві рівнозначні частини, розміщені одна відносно іншої як предмет і його дзеркальне відбиття (рис. 1.9).
Площина симетрії – це площина, яка ділить кристал на дві рівнозначні частини, розміщені одна відносно іншої як предмет і його дзеркальне відбиття (рис. 1.9).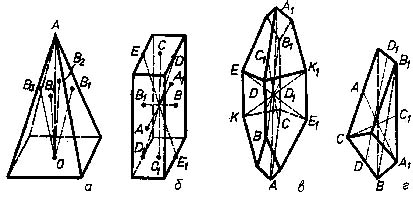 Рисунок 1.10 - Приклади багатогранників з різною кількістю одиничних напрямів: а) - один (ОА); б) - три (АА1, ВВ1, СС1); в) - багато (АА1, ВВ1, СС1, ДД1 та ін.); г) - всі напрями одиничні (АА1, ВВ1 та інші)
Рисунок 1.10 - Приклади багатогранників з різною кількістю одиничних напрямів: а) - один (ОА); б) - три (АА1, ВВ1, СС1); в) - багато (АА1, ВВ1, СС1, ДД1 та ін.); г) - всі напрями одиничні (АА1, ВВ1 та інші) Нижча
Нижча