
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до виконання контрольної роботиСодержание книги
Поиск на нашем сайте
5.1 Перелік питань до першого завдання.
1. Системи стабілізації. 2. Системи програмного керування. 3. Слідкуючі системи. 4. Одноконтурні автоматичні системи. 5. Багатоконтурні автоматичні системи. 6. Автоматичні системи прямої дії. 7. Автоматичні системи непрямої дії. 8. Безперервні автоматичні системи. 9. Дискретні автоматичні системи. 10. Статичні автоматичні системи. 11. Астатичні автоматичні системи. 12. 1зодромні автоматичні системи. 13. Характеристика лінійної автоматичної системи. 14. Характеристика нелінійної автоматичної системи. 15. Аналітичні розрахунки статичних характеристик. 16. Аналітичні розрахунки перехідних характеристик. 17. Графоаналітичний критерій стійкості Михайлова. 18. Частотні характеристики стійкості. 19. Оцінювання стійкості системи за її структурою. 20. Синтез систем автоматичного керування виходячи із умови стійкості. 21. Запас стійкості автоматичної системи. 22. Кореневі методи оцінювання процесів регулювання. 23. Діаграма Вишнеградського. 24. Типові динамічні ланки автоматичних систем. Класифікація та аналіз таких ланок. 25. Особливості нелінійних автоматичних систем. 26. Застосування аналогових та цифрових ЕОМ для оцінювання якості процесів керування.
5.2 Зміст другого завдання
1. Словесний опис механічної системи. 2. Розрахункова схема системи. 3. Математична модель системи:
– диференціальні рівняння; – алгебраїчне рівняння (вихідні диференціальні перетворення за методом Лапласа); − передавальна функція системи (розв'язання системи алгебраїчних
4. Побудова та перетворення структурної схеми системи: − приведення вихідних алгебраїчних рівнянь до вигляду, необхідного для побудови структурної схеми; − структурні схеми, які відображають окремі рівняння; − загальна структурна схема системи; − перетворення структурної схеми за правилами і отримання передавальної функції системи (Зауваження: вирази передавальної функції за п. 3 та 4 повинні бути ідентич-ними); − визначення типових динамічних ланок.
5. Визначення стійкості (для визначення стійкості потрібно використати ПЕОМ або програмний мікрокалькулятор з обов'язковим наведенням програми розрахунку, або, у випадку використання стандартної програми, - на її посилання.):
− за алгебраїчними критеріями; − за графоаналітичним критерієм Михайлова. (Зауваження: а) в роботі потрібно застосувати тільки один алгебраїчний критерій (вибір здійснює викладач); б) визначення стійкості потрібно провести таким чином: - довільно вибрати один з параметрів системи; - визначити стійкість системи для значення цього параметру згідно із завданням на роботу; - визначити стійкість системи ще для двох значень цього параметру, наприклад, одне значення – на порядок нижче заданого значення, друге – на порядок вище.)
6. Визначення частотних характеристик: - амплітудно-частотної (АЧХ); - фазочастотної (ФЧХ); - амплітудно-фазочастотної (АФЧХ).
Зауваження: а) потрібно навести відповідні рівняння, побудувати графіки (бажано з використанням ПЕОМ з обов’язковим наведенням таблиць значень параметрів, за якими будуються відповідні графіки), зробити висновки за результатами аналізу характеристик; б) для визначення характерних зон на АЧХ потрібно задати допустимий діапазон точності роботи даної системи: рекомендовано його задати в межах ±(5÷15%) від значення амплітуди А при ω = 0; в) діапазон кутових частот, для якого потрібно побудувати частотні характеристики, наближено визначається від 0 до 7. Загальні висновки по другому завданню.
5.3 Варіанти завдань до контрольної роботи
5.4 Приклад виконання контрольної роботи
Зміст
1. Словесний опис механічної системи.
2. Розрахункова схема системи.
3. Математична модель системи: а) диференціальні рівняння; б) рівняння перетворення за методом Лапласа (алгебраїчні); в) передавальна функція системи.
4. Побудова та перетворення структурної схеми: а) приведення вихідних рівнянь до побудови структурної схеми; б) структурна схема; в) перетворення структурної схеми за правилами і отримання передавальної функції; г) визначення типових динамічних ланок.
5. Визначення стійкості системи (з використанням ЕОМ): а) за алгебраїчним критерієм; б) за графоаналітичним методом Михайлова.
6. Визначення частотних характеристик з використанням ЕОМ (навести відповідні рівняння, графіки, висновки): а) амплітудно-частотної характеристики; б) фазночастотної характеристики; в) амплітудно-фазночастотної характеристики
7. Загальні висновки по роботі.
1 Словесний опис механічної системи
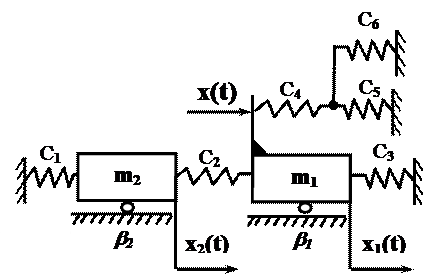
Механічна система складається з таких елементів: − пружина з жорсткістю С − важіль, закріплений на опорі, яка розділяє його на дві частини з довжиною − гільза, що рухається по поверхні з коефіцієнтом в’язкого тертя (демпфування) − гільза складається з пружини жорсткості С Робота системи здійснюється таким чином. Під дією вхідного сигналу X(t) (закон, за яким змінюється сила від джерела енергії) починає деформуватися лівий торець пружини з жорсткістю С1, накопичуючи при цьому енергію, яка здатна перемістити тіло масою m1, тобто перевищити силу тертя спокою цього тіла. Після того, як це тіло починає рухатися по координатному напрямку X1(t), починає рухатися гільза, чому сприяє шарнірне з’єднання тіла масою m1 і гільзи за допомогою важеля. При русі гільзи починає в свою чергу деформуватися лівий торець пружини з жорсткістю С2, накопичуючи енергію для переміщення тіла масою m2 (для подолання опору сили тертя спокою і жорсткості пружини С3). При досягненні цієї умови тіло масою m2 починає рухатися по координатному напрямку X2(t), що являється вихідним сигналом системи.
2 Розрахункова схема механічної системи
  
3 Математичний опис системи а) опис в диференціальній формі Приймаємо припущення: − жорсткість кожної пружини незмінна в часі і кожна пружина деформується за лінійною залежністю; − прикладена зовнішня сила змінюється не дуже швидко, тобто можна знехтувати масою кожної пружини;
− сухе тертя відсутнє; − коефіцієнт в’язкого демпфування незмінний в часі (β); − нехтуємо силою тяжіння; − нехтуємо силами тертя в шарнірних з’єднаннях. Керуючий сигнал у вигляді переміщення Пружна сила Сила інерції
де Тобто, Напрям сили інерції протилежний вектору рушійної сили. Сила, що здійснює опір руху тіла, є силою в’язкого тертя. Сила в’язкого тертя:
Сила в’язкого тертя
де X3(t) – координата переміщення гільзи. Сила пружності пружини з жорсткістю
Запишемо рівняння руху тіла маси
або
Аналогічно складаємо рівняння руху тіла маси
Запишемо рівняння рівноваги важеля:
Рівняння пропорційності переміщень
Отже, математична модель механічної системи, яка записана в диференціальній формі, має вигляд:
б) опис в алгебраїчній формі.
Запишемо вищенаведені рівняння математичної моделі механічної системи в алгебраїчній формі, використавши метод Лапласа, тобто перейдемо від оригіналу x(t) до зображення x(s), де s – оператор Лапласа:
Запишемо перші два рівняння відносно рушійних та збуджуючих сил:
Тоді, остаточна математична модель механічної системи, яка записана в алгебраїчній формі, має вигляд:
в) отримання передавальної функції системи
З урахуванням рівняння (3) рівняння (2) приймає вигляд:
Звідки
Вираз
Враховуючи, що
Отже, передавальна функція системи має такий вигляд:
де
4 Побудова та перетворення структурної схеми
а) приведення вихідних рівнянь до виразів, за якими будуються структурні відображення
Розглянемо рівняння (1). Приймемо для нього:
X(S) – вхідний сигнал, X1(S) - вихідний сигнал.
Запишемо рівняння (1) з врахуванням рівняння (3):
яке відносно вихідного сигналу приймає такий вигляд:
Будуємо структурне відображення рівняння (6):
Для рівняння (3) приймаємо: X1(S) – вхідний сигнал, X3(S) - вихідний сигнал.
Запишемо рівняння відносно вихідного сигналу:
Будуємо структурне відображення рівняння (7):
Для рівняння (2) приймаємо: X3(S) – вхідний сигнал, X2(S) - вихідний сигнал. Запишемо рівняння (2) відносно вихідного сигналу:
Будуємо структурне відображення рівняння (8):
б) побудова загальної структурної схеми
Будуємо загальну структурну схему системи, яка відображає рівняння (1) ÷ (3) (див. рис. 1).
в) перетворення структурної схеми за правилами і отримання передавальної функції системи.
Перетворимо послідовне з’єднання двох ланок:
Рисунок 5.1 – Структурна схема системи
де:
Перетворимо узгоджено-паралельне з’єднання двох ланок:
де:
Перетворимо послідовне з’єднання трьох ланок:
де:
Перетворимо зустрічно-паралельне з’єднання двох ланок:
де: Перетворимо послідовне з’єднання двох ланок:
де:
Виконаємо перетворення для отримання остаточного виразу передавальної функції.
 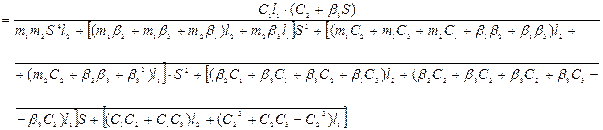
Отриманий вираз передавальної функції (9) після перетворення структурної схеми ідентичний з виразом (5) передавальної функції, яка отримана в п. 3в.
в) визначення типових динамічних ланок
Розглядаючи перехідні характеристики XВИХ Визначимо, з яких же ланок складається отримана структурна схема.
/
Інтегрувальна ланка:
Інерційні ланки другого порядку (коливальні):
Диференціююча ланка (ідеальна) безінерційна:
5 Визначення стійкості системи
Основною динамічною характеристикою автоматичної системи є її стійкість. В залежності від характеру перехідного процесу лінеаризованої системи розрізняють три основних випадки як система себе поводить після збудженого сигналу: − система не може повернутися до рівноважного стану, значення керуючої змінної все більше відхиляється від заданого. Така система така називається нестійкою; − система повертається до рівноважного стану, така система – стійка; − система характеризується встановленим періодичним рухом, такий процес називається незатухаючим коливальним, а система буде знаходитися на межі асимптотичної стійкості.
Запишемо характеристичне рівняння:
Необхідною умовою стійкості системи будь-якого порядку є додатність всіх коефіцієнтів характеристичного рівняння цієї системи. Підпорядкуємо чисельні значення коефіцієнтів а 0, а 1, а 2, а 3, а 4 , використовуючи програму MathCAD:
С 1= 3000 н/м, С 2= 4000 н/м, С 3= 3200 Н/м;
Отже чисельні значення коефіцієнтів:
а 0 = 20, а 2 =3.993∙104, а 4 = 1.464∙107. а 1 = 151, а 3 =1.449∙105,
1. Визначення стійкості системи за алгебраїчними критеріями стійкості
Алгебраїчні критерії стійкості дають можливість за коефіцієнтами стійкості характеристичного рівняння замкнутої системи визначити чи всі корені знаходяться в лівій півплощині, не розв’язуючи цього рівняння.
Критерій Рауса
Запишемо характеристичне рівняння замкнутої системи в чисельному вигляді:
Складаємо таблицю Рауса для цього рівняння.
Отже, система стійка, оскільки всі члени першого стовпчика більші за нуль.
Визначимо стійкість системи використовуючи критерій Гурвіца.
Для рівняння
Знайдемо діагональні мінори:
-
Отже, дана система стійка.
2. Визначення стійкості системи за критерієм Михайлова
Представимо характеристичне рівняння:
Характеристичне рівняння у вигляді функції від S:
Зробивши заміну:
отримаємо рівняння комплексного вектора:
Згідно з критерієм Михайлова лінійна система буде стійкою, якщо крива Михайлова охоплює початок координат та послідовно проходить проти годинникової стрілки n-квадрантів, де n – порядок характеристичного рівняння. Підставляємо в рівняння Графік кривої Михайлова побудуємо за допомогою системи MathCAD:
Рисунок 5.1 – Крива Михайлова
Висновок. Отже визначивши стійкість системи за алгебраїчними критеріями і за критерієм Михайлова можна зробити висновок, що дана механічна система є стійкою при заданих значеннях параметрів.
3. Дослідження впливу параметра m2 на стійкість системи за критерієм Михайлова
Змінивши вихідний параметр масу тіла m2 = 2 кг (див. рис. 5.2), можна зробити висновок, що система є стійкою, збільшивши масу m2 до 20 кг (див. рис. 5.3) запас стійкості збільшується.
Рисунок 5.3 – Крива Михайлова
6 Визначення частотних характеристик системи автоматичного керування
Елементи і системи автоматичного керування можуть піддаватися різним впливам, які характеризуються довільними функціями часу. Зміна положення вихідної ланки системи у вигляді функції часу називається реакцією системи на вхідний вплив. В теорії автоматичного керування широко використовуються методи вивчення динамічних властивостей елементів і системи, які основані на визначенні реакцій, які викликані визначеними (детермінованими) типами впливу. Розглянемо послідовність визначення і розрахунку частотних характеристик лінійної моделі системи. Запишемо передавальну функцію системи, яку ми отримали в п.3:
Позначимо складові в чисельнику як b0, b1, а вирази в знаменнику як а0, а1, а2, а3, а4:
Тоді передавальна функція системи приймає такий вигляд:
Вираз для побудови амплітудно-фазочастотної характеристики (АФЧХ) або комплексної частотної передавальної функції отримаємо з рівняння передавальної функції шляхом підстановки:
Враховуючи, що
Помноживши чисельник і знаменник рівняння на комплексний вираз, спряжений знаменнику, отримаємо:
Таким чином, АФЧХ можна представити у вигляді:
де
Побудуємо графік АФЧХ, тобто залежність P( Графік АФЧХ зображений на рис. 5.4. Вираз для побудови амплітудно-частотної характеристики (АЧХ) системи має такий вигляд:
Графік АЧХ, зображений на рис. 5.5. Вираз для побудови фазочастотної характеристики (ФЧХ) системи отримується в такому вигляді:
Рисунок 5.4 – Амплітудно-фазна частотна характеристика
Рисунок 5.5 – Амплітудно-частотна характеристика: І – робоча зона; ІІ – перша резонансна зона ( ІІІ – перша резонансна зона ( IV – зона фільтрації; заштрихована зона – заданий діапазон точності.
Дійсне значення
де Графік ФЧХ зображено на рис. 5.6
Рисунок 5.6 – Фазочастотна характеристика
Висновок. Отже, використавши побудову амплітудно-фазочастотної характеристики, амплітудно-частотної і фазочастотної характеристик можна отримати інформацію про те, як система реагує на гармонічний сигнал при зміні частоти його подавання на вхід.
Загальні висновки по роботі
Виконавши дану розрахунково-графічну роботу, ми навчилися складати математичну модель механічної системи, також будувати і перетворювати структурну схему. До завдань даної роботи також відносились визначення стійкості системи, визначення і побудова частотних характеристик. За допомогою критерія Михайлова ми визначили стійкість системи, при побудові кривих Михайлова для різних вихідних параметрів (маса m2) можна зробити висновок про те, як змінюється стійкість при зміні його параметра. Побудувавши частотні характеристики АФЧХ, АЧХ і ФАХ можна зробити висновок про те, при яких оптимальних режимах повинна працювати механічна система.
Питання до складання диференційованого заліку з дисципліни 1. Роль автоматизації у сучасному науково-технічному процесі. Перспективи розвитку автоматизації. 2. Основні поняття теорії автоматичного керування (зміст понять: ”керований об’єкт”, ”керована величина”, „простий керований об’єкт”, ”збурюючі діяння”, ”керування об’єктом”, ”керування”, „регулювання”, „автоматичне керування”, ”напівавтоматичне керування”, „автоматичний керуючий пристрій”, „система автоматичного керування”, „блок-схема автоматичної системи з однією керованою величиною”, „задавальне діяння системи”, „вхід”, „вихід системи”, „діяння”, „сигнал”; автоматичне регулювання та керування у живих організмах, природі, техніці, причини, які вимушують усувати людину як слабку ланку в системі керування, етапи розвитку технологічного процесу, місце САК у технологічному процесі; принципи автоматичного керування, принцип керування за відхиленням, поняття „зворотний зв’язок”, функціональна схема САК; принцип керування за збуренням, принцип комбінованого керування; принцип адаптації). 3. Класифікація автоматичних систем (системи стабілізації, програмного керування, слідкуючі, одноконтурні, багатоконтурні, прямої дії, безперервні, дискретні, статичні, астатичні, лінійні, нелінійні). 4. Характеристики автоматичних систем (способи опису роботи автоматичних систем; складання диференціальних рівнянь елементів автоматичної системи; перехід від рівнянь елементів до рівняння автоматичної системи; оцінювання статичних властивостей автоматичної системи; оцінювання динамічних властивостей автоматичної системи). 5. Типові динамічні ланки автоматичних систем (класифікація типових ланок; аналіз типових ланок). 6. Структурні схеми автоматичних систем (поняття структурної схеми; її порівняння з функціональною схемою; передавальна функція окремої ланки; типи з’єднань ланок; правила структурних перетворень; передавальна функція автоматичної системи; зв’язок між замкненою та розімкненою системами). 7. Стійкість автоматичних систем (поняття динамічної стійкості автоматичних системи; математична умова стійкості; алгебраїчні критерії стійкості; графоаналітичні критерії Михайлова; частотний критерій стійкості; оцінювання стійкості системи за її структурою; синтез систем автоматичного керування виходячи із умови стійкості; запас стійкості автомат
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.214.78 (0.015 с.) |

 , де Сå –сумарна жорсткість пружних елементів, må – сумарна маса системи. Крок зміни частот рекомендовано здійснювати методом підбору за візуальним оцінюванням графіка частотної характеристики.
, де Сå –сумарна жорсткість пружних елементів, må – сумарна маса системи. Крок зміни частот рекомендовано здійснювати методом підбору за візуальним оцінюванням графіка частотної характеристики.























 , під дією якої рухається тіло масою m
, під дією якої рухається тіло масою m  ;
;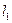 і
і  , відповідно;
, відповідно;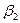 ;
;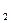 , під дією якої рухається тіло масою m
, під дією якої рухається тіло масою m 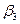 , і пружини жорсткості С
, і пружини жорсткості С  , що сповільнює рух тіла масою m
, що сповільнює рух тіла масою m 

 задається лівому торцю пружини з жорсткістю
задається лівому торцю пружини з жорсткістю  , яка деформується, створюючи пружну силу, що діє на тіло масою
, яка деформується, створюючи пружну силу, що діє на тіло масою  . Величина пружної сили
. Величина пружної сили  дорівнює добутку коефіцієнта жорсткості
дорівнює добутку коефіцієнта жорсткості  .
. являється для тіла масою
являється для тіла масою  ,
, - друга похідна від координати
- друга похідна від координати  переміщення тіла масою
переміщення тіла масою  .
. , або
, або  .
. з коефіцієнтом
з коефіцієнтом  ,
, дорівнює:
дорівнює: .
. ,
,
 .
. . Рушійною силою для тіла маси
. Рушійною силою для тіла маси  ,
, або
або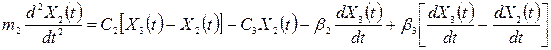 .
. .
. і
і  довжинам плеч:
довжинам плеч: .
.


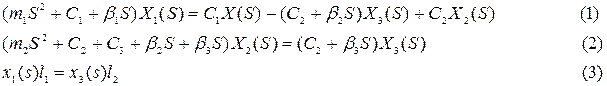

 (4)
(4) підставляємо в рівняння (1) системи, знову ж таки враховуючи рівняння (3):
підставляємо в рівняння (1) системи, знову ж таки враховуючи рівняння (3):

 та вираз (4), отримуємо:
та вираз (4), отримуємо:


 (5)
(5)






 , (6)
, (6)
 ;
;  (7)
(7)
 ;
; . (8)
. (8)




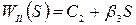

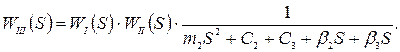



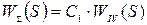 – передавальна функція системи.
– передавальна функція системи.

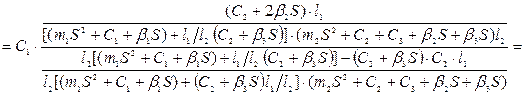

 найпростіших ланок, можна об’єднати ці ланки, подібні за динамічними властивостями в групи, які називаються типовими ланками.
найпростіших ланок, можна об’єднати ці ланки, подібні за динамічними властивостями в групи, які називаються типовими ланками.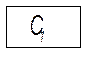 \ ідеальні (безінерційні) ланки, де
\ ідеальні (безінерційні) ланки, де - коефіцієнти підсилення (або передачі)
- коефіцієнти підсилення (або передачі)





 ;
; ;
; ;
; ;
; ;
;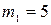 кг,
кг,  кг;
кг; Н∙с/м,
Н∙с/м, 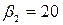 Н∙с/м,
Н∙с/м,  Н∙с/м;
Н∙с/м; м,
м,  0,5 м.
0,5 м.




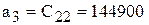


 запишемо визначник Гурвіца:
запишемо визначник Гурвіца: =
=  =
= 
 ;
;
 =
=  ;
; =
=  -
- =
= 
 .
. .
.

 .
. в межах 0…120Гц.
в межах 0…120Гц.







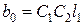 ;
;  ;
;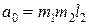 ;
;  ;
; ;
; ;
;


 , запишемо:
, запишемо:







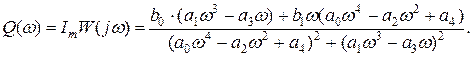





 );
); );
); буде визначатися такими співвідношеннями:
буде визначатися такими співвідношеннями:


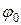 – гострий кут, отриманий за наведеними виразами ФЧХ. Тому при побудові графіка фазочастотної характеристики потрібно вирахувати ці співвідношення.
– гострий кут, отриманий за наведеними виразами ФЧХ. Тому при побудові графіка фазочастотної характеристики потрібно вирахувати ці співвідношення.



