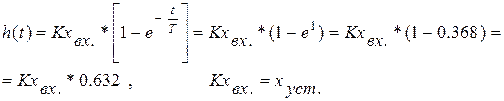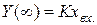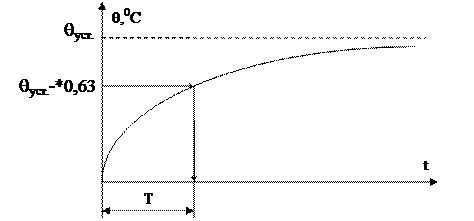Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замедления с помощью шунтирующего сопротивленияСодержание книги
Поиск на нашем сайте Этот метод рассмотрен в п.2.2.2. Его недостаток – дополнительные потери энергии в Rш. Для уменьшения потерь электроэнергии обмотку реле шунтируют диодом (рис. 2.8) В этом случае при отключении реле в контуре реле – диод приобретает ток самоиндукции в направлении прямой проводимости диода и обмотка шунтируется его малым прямым сопротивлением.
а) б) Рис.2.8 Замедление с помощью шунтирующего диода VD а) – схема включения; б) – график переходного процесса Замедление шунтированием обмотки реле емкостью Схема (рис. 2.6) создает замедление не только при включении, но и при отключении. При отключении напряжения емкость Сш разряжается на обмотку реле и обеспечивает замедление спадания тока по сравнению с простым отключением. Графики переходных процессов приведены на рис. 2.9.
Рис. 2.9 Замедление отпускания реле с помощью RC цепи. График переходного процесса
Порядок выполнения работы. 1. Собрать схему (рис. 2.10). Определить напряжение и ток срабатывания реле. Определить напряжение и ток отпускания реле. Примечание: Uном принято равным 24 В, а Iном = 1,35 мА. 2. По данным п.1. определить Кв = 3. Собрать схему, представленную на (рис. 2.10). Определить tср реле для указанных в табл. 1 напряжений. Таблица 2.1.
4. Собрать схему, представленную на (рис. 2.11). Определить реле для указанных в табл. 2.2 напряжений. Подключить в соответствии с рис. 8 диод и для U = Uном определить время отпускания реле. 5. Собрать схему (рис. 2.12) и определить зависимость времени срабатывания реле от величины Rд. При изменении Rд устанавливать ток в обмотке реле. Таблица 2.2
Iр = Iном = 1,35 мА изменением напряжения источника питания. Данные занести в табл.2.3. Таблица 2.3
6. Собрать схему (рис. 2.13) и определить зависимость времени срабатывания реле от величины Rд и Сд. При изменении Rд устанавливать ток в обмотке реле Iр = Iном = 1,35 мА изменением напряжения источника питания. Данные занести в табл.2.4. Таблица 2.4
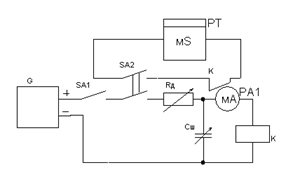
7. Собрать схему (рис. 2.14) и определить зависимость времени срабатывания реле от величины Rд и Сш при Iр = Iном = 1,35 мА. Данные занести в табл. 2.5. Таблица 2.5
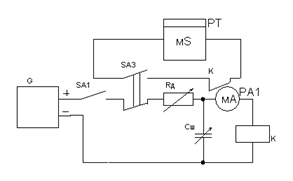
8. Собрать схему (рис. 2.15) и определить зависимость времени отпускания реле от Сш при Iр = Iном = 1,35 мА. Установить Rд = 16,0 кОм для всех значениий Сш. Данные занести в табл. 2.6. Таблица 2.6
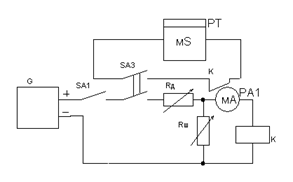
9. Собрать схему (рис. 2.16) и определить зависимость времени срабатывания реле от величин Rд и Rш при Iр = Iном = 1,35 мА. Данные занести в табл. 2.7. Таблица 2.7
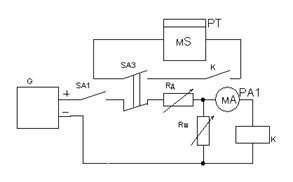
10. Собрать схему (рис. 2.17) и определить зависимость времени отпускания реле от величины Rш Rд = 16,0 кОм и Iр = Iном = 1,35 мА. Данные занести в табл. 2.8. Таблица 2.8
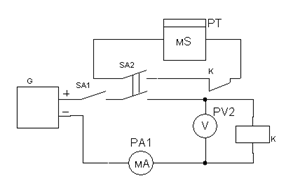
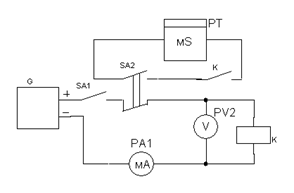
Рис 2.10 Схема для определения Рис. 2.11 Схема для определения времени срабатывания реле времени размыкания реле
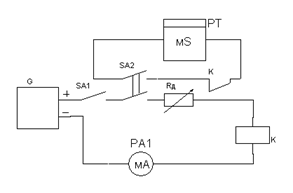
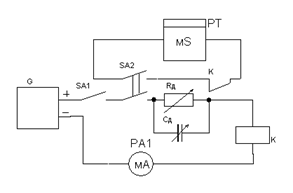
Рис. 2.12 Схема с добавочным Рис. 2.13 Схема с форсирующей сопротивлением (срабатывания) цепью (срабатывания)
Рис. 2.14 Схема с интегрирующей Рис. 2.15 Схема с интегрирующей цепью (срабатывания) цепью (размыкание)
Рис. 2.16 Схема с делителем Рис. 2.17 Схема с делителем напряжения (срабатывания) напряжения(размыкание) Содержание отчета Цель работы. Принципиальные схемы включения реле. Таблицы экспериментальных данных. Графики зависимостей, полученных экспериментально. Выводы по результатам исследований. 2.3. Контрольные вопросы 1. Объяснить принцип действия и назначения элементов конструкции реле. 2. Дать определения времени срабатывания и времени отпускания реле. 3. Привести схемы и объяснить методы ускорения срабатывания реле. 4. Привести схемы и объяснить методы замедления срабатывания реле. 5. Привести схемы и методы замедления отпускания реле. 6. Привести блок-схему и объяснить принцип действия электросекундомера.
Лабораторная работа №3 Экспериментальное определение математической модели объекта регулирования Цель работы: Научиться снимать динамические характеристики объектов, определять тип модели (вид уравнения), коэффициенты модели и передаточную функцию. Общие положения При математическом описании (идентификации) любого объекта управления его поведение можно рассматривать в условиях статики (установившиеся режимы работы) и динамики (переходные режимы). Для условий статики все возмущающие воздействия “f” и все управляющие “u” считаются постоянными величинами, не зависящими от времени. Статические режимы описываются алгебраическими уравнениями, связывающими регулируемые (выходные) параметры “y” с входными воздействиями “f” и “u”.
где j - некоторая векторная функция не зависящих от времени “f” и “u”. Графическое представление зависимости Динамические режимы описываются обычно дифференциальными или интегрально-дифференциальными уравнениями, определяющими зависимость y(t) от изменения воздействий f(t) и u(t).
Различают объекты с самовыравниванием (устойчивые), без самовыравнивания (нейтральные) и неустойчивые. Объект устойчив, если после кратковременного внешнего воздействия он с течением времени стремится к исходному состоянию. Нейтральными называются такие объекты, которые по окончании воздействия стремятся к новому состоянию равновесия, зависящему от величины воздействия. Если управляемая координата y(t) после прекращения воздействия продолжает изменяться, то объект называют неустойчивым. Для составления математической модели объекта используют аналитические и экспериментальные методы. При аналитическом методе составляются уравнения динамики объекта на основе физических законов, определяющих процессы, происходящие в объекте (например, закон сохранения вещества или энергии, закон Кирхгофа и т. п.). Математические выражения соответствующих физических законов, характеризующих поведение объекта, и являются дифференциальными уравнениями, описывающими динамику объекта управления. При аналитическом методе идентификации приходится прибегать в большинстве случаев к идеализации сложных реальных процессов и считать, что объекты обладают детектирующими (однонаправленными) свойствами. Поэтому аналитические методы позволяют лишь приближенно оценить динамические свойства реального объекта. Экспериментальных методов идентификации много, рассмотрим простейшие из них. Для экспериментального определения модели объекта можно использовать временные или частотные динамические характеристики. Временные динамические характеристики представляют собой графики изменения во времени регулируемого (выходного) параметра объекта в зависимости от вида входного воздействия (испытательного воздействия). При подаче в качестве испытательного воздействия дельта-функции d(t) (единичного импульса) получаем импульсную переходную характеристику; уравнение, описывающее эту кривую, называют функцией веса w(t). При подаче на вход объекта единичного ступенчатого воздействия I(t) (единичного скачка), получаем переходную характеристику, ее уравнение - переходная функция h(t). Или иначе: реакция объекта на единичный импульс называется функцией веса w(t), а на единичный скачок - переходной функцией h(t). Достоинство временных характеристик - простота постановки эксперимента. С помощью временных характеристик наиболее просто определяются передаточные функции первого и второго порядка. Идентификация объекта по частотным характеристикам предпочтительнее, т.к. позволяет найти модель и нелинейного объекта, однако требуется более сложный эксперимент. Частотные характеристики показывают изменение модуля и фазы комплексного коэффициента передачи объекта при изменении частоты 0<w<¥. Математическую модель объекта по экспериментально снятым динамическим характеристикам определяют достаточно просто: - по виду графика динамической характеристики, сравнивая его с графиком соответствующей динамической характеристики типовых звеньев, определяют уравнение динамической характеристики, тип дифференциального уравнения динамики объекта; - по динамической характеристике определяют коэффициенты дифференциального уравнения и передаточную функцию объекта. Затем определяют адекватность модели. Математическая модель считается адекватной, если значение параметра на выходе объекта совпадает со значениями, рассчитанными по модели. Постановка эксперимента по снятию временных динамических характерстик. Если экспериментальные исследования проводятся на действующем промышленном объекте, то целесообразно снять импульсную переходную характеристику, т.к. это не вызовет существенного изменения технологических переменных. В остальных случаях можно снимать переходную характеристику. Для записи изменения выходного параметра во времени необходим записывающий вторичный прибор, к которому подключается датчик (первичный преобразователь). Если снимается временная динамическая характеристика теплового объекта, то выходным параметром является температура. Возмущающее воздействие для теплового объекта с электрообогревом можно создать изменением напряжения, подаваемого на нагревательный элемент. Для снятия импульсной переходной характеристики необходимо резко увеличить напряжение на некоторую величину и через некоторое время (выбирается в зависимости от свойств объекта) снова снизить его до первоначального уровня. Реакция на импульс для инерционного объекта будет иметь следующий вид (рис. 3.1):
Рис. 3.1 График импульсной переходной характеристики
где К- коэффициент передачи; Т - постоянная времени, оценивает инерционные свойства объекта и показывает, за какое время закончился бы переходный процесс, если бы он шел с постоянной скоростью. Практически же переходный процесс заканчивается за время, равное t=(3¸4)Т. Для снятия переходной характеристики теплового объекта необходимо резко изменить (увеличить) напряжение, подаваемое на нагревательный элемент, т.е. изменять входной сигнал в виде ступеньки. Реакция на единичное ступенчатое воздействие и есть переходная характеристика для инерционного объекта. (рис. 3.2). Коэффициент передачи К определяется следующим образом:
Рис. 3.2 График переходной характеристики для инерционного объекта
Постоянная времени Т может быть определена: а) по реакции подкасательной на линию установившихся значений (касательная может проводиться в любой точке) - если кривая – экспонента (рис.3.2); б) по проекции подсекущей на линию установившегося значения (рис. 3.3).
Рис. 3.3 Получение Т методом подсекущей
Если y(t) не имеет точек перегиба и представляет собой экспоненту, то исследуемый объект управления является инерционным первого порядка и уравнение имеет вид: При t=T:
Согласно уравнению переходной характеристики, за время, равное T, переходный процесс заканчивается на 0,63 своего установившегося значения (рис. 3.4). После завершения переходного процесса на выходе объекта управления установившееся значение: Кхвх.=h(¥)=Y(¥). Следовательно, если нет запаздывания, то постоянную времени можно определить и таким образом:
Рис 3.4
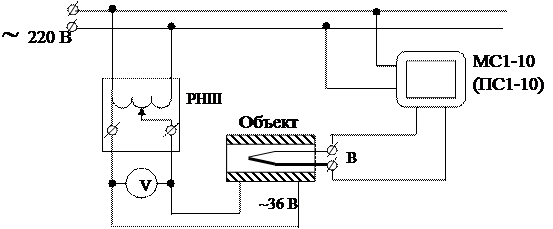
Порядок выполнения работы 1. Собрать схему лабораторной установки, изображенной на рис.3.5. 2. Снять переходную характеристику, для чего на объект подать напряжение 36В (подключить нагревательный элемент к сети). 3. Определить математическую модель объекта регулирования, сравнивая полученную переходную характеристику с характеристиками типовых звеньев. 4. Определить коэффициенты модели T и K и передаточную функцию W(p).
Рис. 3.5 Схема лабораторной установки
Содержание отчета Цель работы. Схема лабораторной установки. График переходной характеристики. Математическая модель и коэффициенты. Выводы по результатам исследований.
3.3. Контрольные вопросы 1. Что такое математическая модель и как она может быть экспериментально получена? 2. Определение математической модели теплового объекта и ее коэффициентов. 3. Что такое Т, как определяется и что означает? 4. Что такое К, как определяется и что означает? Лабораторная работа № 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |




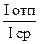 и Кз =
и Кз = 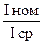 .
.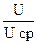
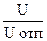
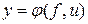 ,
,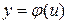 и возмущения
и возмущения 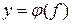 .
.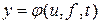 .
.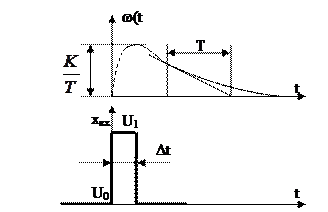
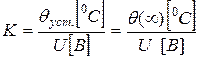 .
.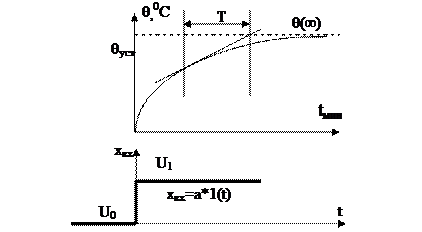
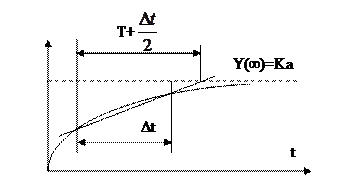
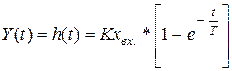 .
.