Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Міст Уітстона. Загальна теорія мостових схемСодержание книги
Поиск на нашем сайте
Мостові засоби вимірювань
Мостові схеми застосовуються для вимірювання параметрів електричних кіл, а також для вимірювання неелектричних величин сумісно з параметричними вимірювальними перетворювачами. Мостовим називають електричне коло, в якому можна виділити два розгалуження опорів, значення між якими дорівнює нескінченності при відповідному співвідношенні параметрів елементів кола, і скінченому значенню, якщо це співвідношення не виконується. Засіб вимірювання, в основу якого покладено мостове коло, називають вимірювальним мостом. Вимірювальні мости класифікують за такими ознаками: - за родом струму, що живить мостове коло, виділяють мости постійного і змінного струму; - за архітектурою побудови – чотири- і багатоплечі; - за способом зрівноваження – автоматичні та з ручним зрівноваженням.
Міст Уітстона. Загальна теорія мостових схем
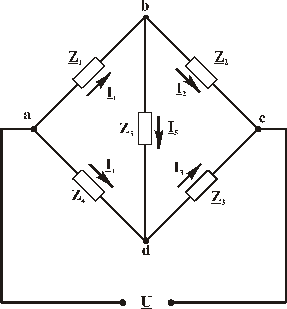
Для з’ясування принципів побудови мостових схем найчастіше використовують міст Уітстона, схема якого подана на рис.3.13.
Такий міст має чотири опори: Z1, Z2, Z3, Z4. Точки a, b, c, d називають вершинами моста. Електричне коло між двома суміжними вершинами називають плечем моста (Z1,Z2,Z3,Z4 – плечі моста). Електричне коло між двома протилежними вершинами називають діагоналлю моста (ас – діагональ живлення, вd – вимірювальна діагональ). В коло вимірювальної діагоналі вмикається індикатор рівноваги ІР, внутрішній опір якого Z5.
Рисунок 3.13
Виведемо умову рівноваги для моста Уітстона. Міст вважається зрівноваженим, коли струм I5 у вимірювальній діагоналі відсутній (I5=0). Отже, у зрівноваженій схемі потенціали точок в і d однакові (точки в і d еквіпотенціальні). Однакові і спади напруг на першому і четвертому плечах, оскільки точка а є для них загальною:
Те саме справедливе і для напруг на другому і третьому плечах моста:
У зрівноваженому мостовому колі
а
Розділимо почленно (3.19) на (3.20) і одержимо умову рівноваги:
З (3.23) отримаємо умови рівноваги для мостів змінного струму. Записавши комплексні опори в показниковій формі, одержимо:
З (3.24) матимемо дві умови рівноваги
Рівняння (3.25) показують, що умова рівноваги моста змінного струму складається завжди із двох частин – (а) та (б). Тому для зрівноваження моста він повинен мати два регульованих елемента, які дозволяють змінювати модуль та аргумент комплексного числа. Зрівноваження моста змінного струму здійснюється почерговим регулюванням двох елементів. Число регулювань, необхідних для досягнення рівноваги моста, визначає так звану “збіжність” моста. Кількісно “збіжність” моста не оцінюється, оцінюється “збіжність” тільки якісно: хороша (швидка) “збіжність” чи погана “збіжність”. На постійному струмі опори мостової схеми є чисто активними: Z1 = R1, Z2 = R2, Z3 = R3, Z4 = R4. Тому мостова схема на постійному струмі буде зрівноваженою, коли виконується умова рівноваги
Порівнявши умови рівноваги (3.25) і (3.26) можна дійти висновку, що для зрівноваження мостів на змінному струмі необхідно досягти дві умови рівноваги (3.25), а на постійному тільки одну (3.26). В цьому і є основна особливість зрівноваження мостів постійного і змінного струму. Вимірювальні мости постійного струму
Мости постійного струму застосовуються для вимірювання активних опорів і для вимірювання неелектричних величин сумісно з резистивними параметричними вимірювальними перетворювачами. З мостів постійного струму практичне розповсюдження одержали чотириплечий (одинарний) та шестиплечий (подвійний) мости. Одинарний (чотириплечий) міст постійного струму Схема моста наведена на рис.3.14. Міст живиться від джерела постійного струму (в діагоналі живлення знаходиться джерело живлення з е.р.с. E та внутрішнім опором R0). У вимірювальній діагоналі ввімкнено індикатор рівноваги (ІР).
Рисунок 3.14
Використавши (3.26) запишемо умову рівноваги для одинарного моста:
Процес вимірювання за допомогою одинарного моста полягає в тому, що в одне з плечей (наприклад, R1) вмикають вимірюваний опір Rx. Тоді на основі наведених викладок запишемо умову рівноваги:
З (3.28) знайдемо:
де R2, R4 – плечі відношення, R3 – плече порівняння. Із (3.29) видно, що значення опору Rx порівнюється із значенням опору R3 в масштабі Вимірюваний опір приєднується до затискачів моста за допомогою провідників. Крім того, є опір ізоляції між затискачами моста. З урахуванням цього схема моста може бути представлена у вигляді, зображеному на рис.3.15. Uж – напруга живлення моста, Rп1 та Rп2 – опори підвідних проводів та контактів, Rіз – опір ізоляції. Можна прийняти Rп1 = Rп2 = Rп. Якщо проводи виготовлені із міді, мають переріз ³ 1 мм2 та невелику довжину, то сумарний опір 2Rп £ 0,01 Ом. При вимірюванні низькоомних опорів Rіз можна не враховувати. В цьому випадку сумарний опір плеча a–c
де d1 = 2Rп/Rx – відносна похибка вимірювання опору Rх, обумовлена проводами та контактами. Щоб похибка d1 була меншою 0,1%, тобто d1 = 2Rп/Rx £ 10–3, Rx повинно бути не менше 2Rп×103 = 0,01×103 = 10 Ом. Отже, Rxн = 10 Ом – нижня межа вимірюваних опорів за цих умов. Виходячи з того, що Rіз = 1011–1016 Ом, розмірковуючи аналогічно, одержуємо при Rіз = 1011 Ом верхню межу Rxв £ 108 Ом. Рисунок 3.15 Нижню межу можна значно знизити, якщо застосовувати чотириполюсне приєднання вимірюваних опорів (рис.3.16).
Рисунок 3.16
Вимірюваний опір має чотири затискачі: С–С – струмові затискачі, які мають велику площу контактів, П–П – потенціальні затискачі, r1, r2, r3 та r4 – опори підвідних проводів. Опори r1 та r3 знаходяться в діагоналях моста, в умову рівноваги вони не входять, отже, похибку в результати вимірювання не вносять. Дещо вони впливають на чутливість моста, але дуже мало. Опори r2 та r4 вмикаються послідовно з R3 та R2, і якщо R3 та R2 більші 10 Ом, то похибка від впливу r2 та r4 буде малою. При чотириполюсному (чотирипровідному) підключенні вимірюваних опорів нижня границя моста знижується до 10‑4 Ом.
В мостах передбачаються перемички (або перемикачі), за допомогою яких можна здійснювати дво- або чотириполюсне приєднання вимірюваних опорів. Рисунок 3.17 Вимірюваний опір Rx та зразковий RN мають по чотири затискачі. R – опір короткого та товстого провідника, який з’єднує Rx та RN. Він включає в себе опори перехідних контактів. Значення цього опору дуже мале. Для одержання рівняння рівноваги перетворимо трикутник опорів R3‑R‑R4 в еквівалентну зірку:
Після цього отримуємо чотириплечий міст, умова рівноваги для якого має вигляд:
(Rx + R3R)×R2 = R1×(R4R + RN), Rx×R2 = R1×R4R + R1×RN – R2×R3R. Підставимо в (3.31) формули для опорів еквівалентної зірки: Rx×R2 = звідки Rx = RN× З (3.32) видно, що Rx залежить від R, який входить у другу складову і має дуже мале значення опору. Другу складову можна виключити (зробити її рівною нулю), якщо виконати умову: (R1×R4/R2)-R3 = 0. Але точно витримати цю умову на практиці не вдається через неточності виготовлення резисторів R1, R2, R3, R4. І для того, щоб друга складова була якомога меншою, потрібно, щоб опір R був як можна меншим. Тоді можна прийняти другу складову в рівнянні (3.32) рівною нулю і вважати що Rx = Для того, щоб (R1×R4/R2)–R3 = 0, намагаються забезпечити рівності R1 = R4 та R2 = R4. Для цього R1 та R3, а також R2 та R4 змінюють одночасно за допомогою однієї регулювальної рукоятки. Як уже відмічалось, подвійний міст застосовується для вимірювання малих опорів. Але при малих Rx та RN і спади напруг на них малі (£1 мВ), тому потрібно враховувати дію термо-е.р.с., які виникають в потенціальних контактах Rx та RN. Для зменшення похибки від термо-е.р.с. виконують два вимірювання при двох напрямках струму, які встановлюють за допомогою перемикача SA. Результат вимірювання Rx визначають як середнє арифметичне двох вимірювань. Промисловість випускає комбіновані мости, в яких за допомогою простих перемикань можна одержати одинарний та подвійний мости.
Рисунок 3.18 Для послідовної схеми tgd = I×Rx/(I/wCx) = wRxCx; для паралельної tgd = IR/IC = (U/Rx)/(U×wCx) = 1/w×Rx×Cx. Виходячи зі схем заміщення конденсаторів в табл.3.1 наведено повні опори плеч мостів для вимірювання ідеальної ємності та ємності конденсаторів з малими і великими втратами. Таблиця 3.1 – Повні опори плеч мостових схем
На прикладі моста для вимірювання ємності з малими втратами наведемо загальну методику виведення умови рівноваги для мостів змінного струму. 1. Введемо такі позначення:
2. Використавши позначення (3.34) запишемо умову рівноваги для даного моста
3. Отримаємо залежності для повних опорів кожного із позначених плечей моста Z x =Rx + 1/jwCx; Z 2 =R2; Z 3 =R3 + 1/jwC3; Z 4 =R4. (3.36) 4. Підставимо (3.36) в (3.35) і матимемо:
5. Розкриємо дужки в (3.37):
Рівність (3.38) є рівністю двох комплексних чисел. А два комплексних числа будуть рівні тоді, коли рівні їх дійсні і уявні частини. 6. Прирівняємо дійсні частини (3.38)
і знайдемо
Оскільки Rx порівнюється з R3 у співвідношенні 7. Прирівняємо уявні частини (3.38)
і знайдемо
Для зрівноваження моста конденсатор С3 має бути конденсатором змінної ємності. 8. Знаходимо тангенс кута втрат tgd = wRx×Cx = wR3×C3. (3.43)
Застосувавши наведену методику і формули (табл.3.1) для повних опорів мостів для вимірювання ємності конденсатора в табл.3.2 наведено кінцеві вирази для визначення Rx і Cx. Міст з послідовною схемою заміщення застосовується для вимірювання параметрів конденсаторів з малими втратами, з паралельною схемою – для конденсаторів з великими втратами. Таблиця 3.2 – Аналітичні залежності
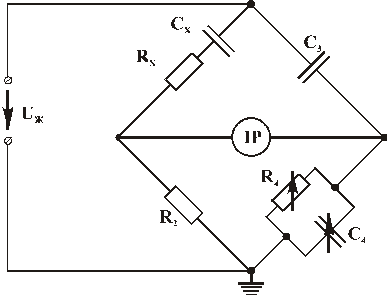
Електричний кабель, наприклад, одножильний, складається із жили, яка розташовується по осі кабеля, та металевої оболонки. Між жилою та оболонкою знаходиться діелектрик. Жила та оболонка кабеля, таким чином, являють собою конденсатор. Випробування кабеля проводяться при напрузі, під якою він знаходиться під час експлуатації. При випробуваннях визначають ємність кабеля та tgd (які потім перераховують на одиницю довжини). В процесі випробувань високовольтних кабелів на вимірювальний міст доводиться подавати високу напругу. Для цього випадку призначена схема моста на рис.3.20, яка забезпечує не тільки вимірювання параметрів кабелю, а й безпеку роботи.
Рисунок 3.20
Параметри елементів моста підбираються так, щоб основна частина високої напруги припадала на верхні елементи схеми (Cx–Rx, C3), а регульовані оператором елементи C4 та R4 були під низькою напругою. Ці елементи заземлюють. Виходячи з наведеної раніше методики отримано формули, за якими обчислюються шукані параметри: Rx = R2×(C4/C3); Cx = C3×(R4/R2); (3.44) tgd = wRx×Cx = wR4×C4. Рисунок 3.21
Котушка індуктивності, параметри якої вимірюються, вмикається в одне з плечей моста. Щоб міст можна було зрівноважити, хоча б одне з пліч, що залишились, повинно містити або змінну індуктивність, або змінну ємність. Найчастіше застосовують змінну ємність, оскільки конденсатор змінної ємності можна виготовити з більшою точністю та з меншими затратами, ніж котушку зі змінною індуктивністю. Схема моста приведена на рис.3.22,а. Умова рівноваги для даного випадку запишеться у вигляді: Rx + jwLx = або після перемноження та ділення правої частини на jwC4: Rx + jwLx = звідки Rx = Добротність котушки Q=wLx/Rx=wR4C4. Зрівноважується такий міст регулюванням R3 та R4. Але, як видно з виразів для Rx та Lx, при виконанні однієї рівності регулюванням (наприклад, рівності Lx=R2×R3×C4) порушується інша (яка досягається регулюванням R4).
Рисунок 3.22
Недоліком цієї схеми моста є погана збіжність, особливо при низьких добротностях котушки. Якщо Q = 1, процес зрівноважування вже викликає труднощі, а при Q < 0,5 зрівноважування моста практично неможливе. Вимірювання параметрів котушок індуктивності з низькою добротністю відбувається за допомогою шестиплечого моста (рис.3.22,б). Для одержання умови рівноваги цього моста потрібно трикутник, створений елементами R4, R5 та C, перетворити в зірку. Після такого перетворення виходить чотириплечий міст, умова рівноваги якого відома. З неї випливає вираз для знаходження параметрів котушки (одержати самостійно). Міст зрівноважується регулюванням R4 та R5. Спочатку регулюванням R4 добиваються виконання першої умови рівноваги, потім регулюванням R5 міст наближається до умови рівноваги. R5 не впливає на першу умову, тому міст має хорошу збіжність.
Рисунок 3.23 Автоматичні мости постійного струму мають основну зведену похибку ±(0,25¸1)%. В автоматичних мостах змінного струму необхідно для досягнення рівноваги регулювати два елементи. Через це та в силу інших причин автоматичні мости змінного струму поступаються точністю автоматичним мостам постійного струму. Мостові засоби вимірювань
Мостові схеми застосовуються для вимірювання параметрів електричних кіл, а також для вимірювання неелектричних величин сумісно з параметричними вимірювальними перетворювачами. Мостовим називають електричне коло, в якому можна виділити два розгалуження опорів, значення між якими дорівнює нескінченності при відповідному співвідношенні параметрів елементів кола, і скінченому значенню, якщо це співвідношення не виконується. Засіб вимірювання, в основу якого покладено мостове коло, називають вимірювальним мостом. Вимірювальні мости класифікують за такими ознаками: - за родом струму, що живить мостове коло, виділяють мости постійного і змінного струму; - за архітектурою побудови – чотири- і багатоплечі; - за способом зрівноваження – автоматичні та з ручним зрівноваженням.
Міст Уітстона. Загальна теорія мостових схем
Для з’ясування принципів побудови мостових схем найчастіше використовують міст Уітстона, схема якого подана на рис.3.13.
Такий міст має чотири опори: Z1, Z2, Z3, Z4. Точки a, b, c, d називають вершинами моста. Електричне коло між двома суміжними вершинами називають плечем моста (Z1,Z2,Z3,Z4 – плечі моста). Електричне коло між двома протилежними вершинами називають діагоналлю моста (ас – діагональ живлення, вd – вимірювальна діагональ). В коло вимірювальної діагоналі вмикається індикатор рівноваги ІР, внутрішній опір якого Z5.
Рисунок 3.13
Виведемо умову рівноваги для моста Уітстона. Міст вважається зрівноваженим, коли струм I5 у вимірювальній діагоналі відсутній (I5=0). Отже, у зрівноваженій схемі потенціали точок в і d однакові (точки в і d еквіпотенціальні). Однакові і спади напруг на першому і четвертому плечах, оскільки точка а є для них загальною:
Те саме справедливе і для напруг на другому і третьому плечах моста:
У зрівноваженому мостовому колі
а
Розділимо почленно (3.19) на (3.20) і одержимо умову рівноваги:
З (3.23) отримаємо умови рівноваги для мостів змінного струму. Записавши комплексні опори в показниковій формі, одержимо:
З (3.24) матимемо дві умови рівноваги
Рівняння (3.25) показують, що умова рівноваги моста змінного струму складається завжди із двох частин – (а) та (б). Тому для зрівноваження моста він повинен мати два регульованих елемента, які дозволяють змінювати модуль та аргумент комплексного числа. Зрівноваження моста змінного струму здійснюється почерговим регулюванням двох елементів. Число регулювань, необхідних для досягнення рівноваги моста, визначає так звану “збіжність” моста. Кількісно “збіжність” моста не оцінюється, оцінюється “збіжність” тільки якісно: хороша (швидка) “збіжність” чи погана “збіжність”. На постійному струмі опори мостової схеми є чисто активними: Z1 = R1, Z2 = R2, Z3 = R3, Z4 = R4. Тому мостова схема на постійному струмі буде зрівноваженою, коли виконується умова рівноваги
Порівнявши умови рівноваги (3.25) і (3.26) можна дійти висновку, що для зрівноваження мостів на змінному струмі необхідно досягти дві умови рівноваги (3.25), а на постійному тільки одну (3.26). В цьому і є основна особливість зрівноваження мостів постійного і змінного струму.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.145 (0.014 с.) |

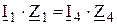 . (3.19)
. (3.19)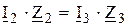 . (3.20)
. (3.20)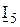 =0, отже,
=0, отже,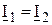 , (3.21)
, (3.21)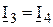 . (3.22)
. (3.22)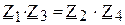 . (3.23)
. (3.23)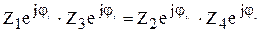 . (3.24)
. (3.24)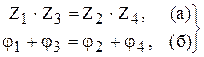 . (3.25)
. (3.25)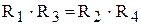 . (3.26)
. (3.26)
 . (3.27)
. (3.27) . (3.28)
. (3.28)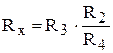 , (3.29)
, (3.29) . Тому міст приводиться в рівновагу регулюванням опору R3, а R2/R4 – масштабний множник, значення якого вибирається рівним 10n, де n – ціле додатне або від’ємне число, або n = 0. R3 називають плечем зрівноваження, R2 та R4 – плечі відношення (з їх допомогою вибирається межа вимірювання моста).
. Тому міст приводиться в рівновагу регулюванням опору R3, а R2/R4 – масштабний множник, значення якого вибирається рівним 10n, де n – ціле додатне або від’ємне число, або n = 0. R3 називають плечем зрівноваження, R2 та R4 – плечі відношення (з їх допомогою вибирається межа вимірювання моста). R1 = Rx + 2Rп = Rx(1 + d1), (3.30)
R1 = Rx + 2Rп = Rx(1 + d1), (3.30)
 .
. + R1×RN –
+ R1×RN –  ,
, +
+  . (3.32)
. (3.32)

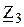
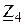
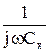
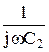
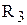
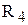

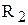
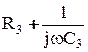
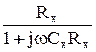
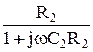
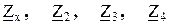 (3.34)
(3.34)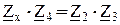 . (3.35)
. (3.35)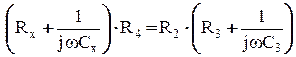 . (3.37)
. (3.37)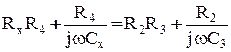 . (3.38)
. (3.38)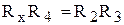 (3.39)
(3.39)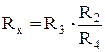 . (3.40)
. (3.40)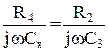 (3.41)
(3.41)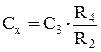 . (3.42)
. (3.42)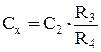
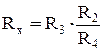
 , (3.45)
, (3.45)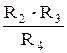 ×(jwR4C4), (3.46)
×(jwR4C4), (3.46)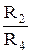 ×R3; Lx = R2×R3×C4. (3.47)
×R3; Lx = R2×R3×C4. (3.47)