Перспектива плоских предметов и геометрических тел

Самые различные предметы огра­ничены совокупностью пересекаю­щихся между собой плоских поверх­ностей. Поэтому, чтобы быстро на­учиться построению перспективы таких предметов, следует познако­миться прежде всего с построением в перспективе прямоугольных пло­ских предметов, а затем для этих же целей полезно предварительно изучить перспективное построение геометрических тел. Геометрические тела: куб, цилиндр, призма — являются самыми простыми форма­ми, лежащими в основе строения всех предметов. Основная форма древесного ствола — цилиндр, арбу­за или яблока — шар, форма кув­шина основана на соединении форм шара и цилиндра. Куб является ос­новой строения предметов, ограни­ченных плоскими поверхностями.

Конструкции самых сложных предметов могут быть представлены в виде совокупности простейших геометрических тел. Фигуры животных, сложные формы растений, на первый взгляд представляющиеся неопределенными, также можно раз­бить на простые формы.

На примере геометрических тел легче всего усвоить законы построения перспективы. Умение свободно строить куб и цилиндр в перспек­тиве (с любой точки зрения и в лю­бом положении по отношению к ли­нии горизонта) дает возможность легко и грамотно нарисовать с на­туры любой предмет, ограниченный плоскостями, или любой предмет цилиндрической или конической формы, а также интерьер и панора­му города.

Рисование прямоугольника, рас­положенного в вертикальном поло­жении. Возьмем прямоугольную дос­ку незначительной толщины и поста­вим ее под углом к рисующему так, чтобы линия горизонта проходила несколько ниже середины модели (рис. 4). Приступая к построению перспективы данного предмета, мы должны сначала определить его про­порции: во сколько раз видимая высота больше видимой ширины. Пропорциональное отношение этих размеров необходимо построить на рисунке. Для этого произвольно на­мечаем на бумаге высоту ближай­шей вертикальной стороны доски. Эта высота служит масштабом ри­сунка. По ней можно определить ширину предмета, если предвари­тельно методом визирования, а луч­ше на глаз узнать в натуре, сколь­ко раз видимая ширина доски укла­дывается в высоте. Эти отношения выдерживаем на рисунке в умень­шенном масштабе. Таким образом, мы определили размер, границы ри­сунка и пропорции основных частей (прямоугольника abed). Хотя по­строение прямоугольника идет лини­ей, однако, рисуя линией, надо мыс лить формой, заключающейся между линиями. Наблюдая модель прямоугольни­ка, мы воспринимаем его ближай­шее вертикальное ребро несколько больше, чем дальнее; параллельные ребра, уходящие вглубь, мы видим наклонными; ребро, расположенное ниже горизонта, как будто подни­мается, а ребро, расположенное вы­ше, опускается к линии горизонта. Наклоны этих линий в натуре изме­ряются относительно горизонтально­го направления, как показано на рис. 3. Найденные углы намечаем на ри­сунке наклонными прямыми, которые при продолжении должны пересечь­ся в одной точке на линии горизон­та. Точка пересечения может нахо­диться далеко за пределами листа бумаги. Когда общий прямоуголь­ник доски будет нарисован, намеча­ем толщину доски.

Рисование прямоугольника, рас­положенного в горизонтальном поло­жении. Моделью будет служить та же прямоугольная доска, располо­женная горизонтально ниже линии горизонта, ближайшая сторона (аЪ) которой перпендикулярна направле­нию зрения (рис. 5). Прежде всего определим видимые пропорции до­ски: что меньше, длина (горизон­тальное направление) или ширина (вертикальное направление). Эти пропорции необходимо передать на рисунке. Чтобы определить направ­ление боковых сторон, по очереди на­ведем со своего места вертикально взятый карандаш на точки а и ь и определим видимые углы между ка­рандашом и краями доски. Эти углы строим на рисунке. Боковые стороны доски при продолжении должны пе­ресечься в точке, лежащей на линии горизонта.

Толщину доски можно нанести одновременно с построением общей формы, предварительно сравнив ее с длиной и шириной. Правильность построения зависит от точной пере­дачи пропорций, ширины и длины доски, а также от угла накло­на уходящих вдаль горизонтальных сторон.

Видоизменим это упражнение: возьмем вместо доски книгу и рас­положим ее под углом к рисующему. Построение перспективы в этом слу­чае надо вести так: провести пря­мую, параллельную нижнему краю листа бумаги, и от нее наметить на­правление двух ближних горизон­тальных ребер книги. Когда направления найдены, на этих линиях откладывается длина левой и правой грани и тем самым опреде­ляется нижнее основание предмета. Параллельные в натуре ребра книги на рисунке должны быть сходящими­ся (при продолжении) в одной точ­ке на линии горизонта слева и справа от рисунка. Затем определяется высота книги и строится ее верхняя горизонтальная грань (рис. 6).

Упражнение. Перспективное построение прямоугольного предмета в вертикальном и горизонтальном положении следует повторить не­сколько раз, перемещая модель вы­ше линии горизонта, ниже и поворачивая ее под разными углами к рисующему. При этом особое вни­мание надо обращать на взаимные пропорции граней: ширины, длины и высоты, а также на изменение вели­чины углов наклона горизонтальных сторон в зависимости от поворота модели в пространстве и расстоя­ния от нее до линии горизонта. В противном случае рисунок будет неправдивым.

Перспективное построение куба.

Поставим куб ниже линии горизонта и повернем его так, чтобы левая и правая боковые грани его не казались равными по ширине.

Всякому рисованию предшеству­ет изучение конструкции и перспек­тивных изменений формы предмета в натуре. Только хорошо изученный предмет можно нарисовать правиль­но. В данном случае необходимо понять соотношение видимых раз­меров граней и ребер куба, опреде­лить, какая из вертикальных граней открыта больше, какая меньше.

Грани куба представляют основу всей конструкции его, поэтому с них следует начинать построение. Чтобы построить перспективу составляю­щих куб плоскостей, надо начинать рисовать с ближнего плана, с бли­жайшего вертикального ребра. Вы­соту его наносим произвольно в зависимости от величины листа бумаги (рис. 7).

От верхнего и нижнего конца это­го вертикального ребра проводим направления нижних и верхних го­ризонтальных ребер, предварительно определив углы наклона этих ребер в натуре. У куба, который расположен целиком ниже линии горизонта, угол наклона нижних горизонталь­ных ребер будет больше, чем верхних, причем у большей (более от­крытой) видимой вертикальной грани угол наклона уходящих горизон­тальных ребер будет меньше, и на­оборот, у меньшей грани—больше. Горизонтальные параллельные ребра сходятся в точках, лежащих на. ли­нии горизонта слева и справа от ри­сунка, в данном случае далеко за пределами листа бумаги, поэтому мы не можем с их помощью делать построение горизонтальных ребер. Важно, чтобы на рисунке было за­метно, что параллельные в натуре ребра, если мысленно продолжить их, сойдутся на линии горизонта.

Определив направление нижних и верхних горизонтальных ребер, проводим два крайних вертикальных ребра левой и правой грани куба и таким образом намечаем видимую величину вертикальных граней. При этом надо строго следить за взаим­ными пропорциями ширины этих гра­ней и высоты ближайшего верти­кального ребра. От правильного построения углов наклона горизон­тальных ребер куба и соблюдения пропорций видимых размеров граней зависит правильность дальнейшего изображения.

При построении простейших гео­метрических тел нельзя изображать только видимые их стороны без уче­та сторон, скрытых от глаз. Без по­нимания всей конструкции в целом изображаемые предметы будут вы­глядеть односторонними. Поэтому «замкнув» ребрами две видимые вер­тикальные грани, строим верхнее и нижнее основания куба. Горизон­тальные ребра, идущие в одном на­правлении, должны на рисунке сходиться (при продолжении) в од­ной и той же точке схода, лежащей на линии горизонта. Следить надо также за шириной (разворотом) верхнего и нижнего оснований.

 

Необходимо сделать не одно, а несколько построений куба с натуры, при этом куб надо ставить в различ­ных положениях: ниже, выше линии горизонта и в разных поворотах. В каждом отдельном случае необ­ходимо определять пропорции гра­ней и наклоны ребер. При этом все внимание должно быть направлено не на очертание куба, а на всю фор­му в целом, на перспективу состав­ляющих ее плоскостей.

Одновременно с построением не­обходимо намечать и светотень куба. Рисующий без труда может заме­тить, что при боковом освещении са­мой темной гранью куба является одна из его вертикальных боковых граней. Затем надо сравнить осталь­ные грани и определить, какая из них темнее — верхняя или освещен­ная боковая. Следует нанести и тень, падающую от куба на горизонталь­ную плоскость. Как правило, она бу­дет несколько темнее теневой грани куба. Постепенно усиливая и посто­янно сравнивая по светлоте эти три грани куба и падающую тень, ри­сующий добивается правильной пе­редачи освещения и наиболее точ­ного выявления объемной формы, их пропорций и композиционного раз­мещения.

Освоив рисование куба в различ­ных поворотах, обучающийся может перейти к рисованию параллелепипе­да и. различных предметов быта пря­моугольной формы (прямоугольные ящики, коробки, книги, чемоданы). Хорошим упражнением будет рисо­вание табурета в различных пово­ротах.

При построении всех этих пред­метов нужно стремиться к тому, что­бы рисование начиналось не с сере­дины или конца этапа, а с нача­ла, с основания. Любой пред­мет всегда стоит или лежит на горизонтальной плоскости. А горизон­тальная плоскость всегда уходит в глубину от рисующего. Таким обра­зом, начиная перспективно строить предмет с основания, рисующий изображает одновременно эту уходящую в глубину горизонтальную плоскость и решает сразу несколько задач: ставит предмет на горизон­тальную плоскость, настраивает себя с самого начала работы на передачу глубины и, самое главное, осуществ­ляет объемный, конструктивный, со­знательный подход к изображению предмета.

Вот почему, рисуя такие предме­ты, как ящик, коробку, чемодан, всегда нужно начинать построение не с верхней грани, а с той грани, которая не видна, но которая на­ходится на горизонтальной плоско­сти ближе и является основанием, фундаментом,. Например, рисунок табурета, стоящего на полу, начи­нают не с сиденья, а с условного квадрата, в вершинах которого стоят ножки табурета. Этим самым табу­рет сразу ставится на горизонталь­ную плоскость и определяется его разворот в пространстве (рис. 8).

Такой же конструктивный подход необходим при рисовании более сложных геометрических тел: приз-

мы и пирамиды. Конструкция шести­угольной призмы гораздо сложнее, чем конструкция куба. Ее изучение лучше начинать с рисования прово­лочного каркаса.

 

Круг в перспективе. Наибольшую трудность при рисовании цилиндра

в перспективе представляет изображение круглых оснований, поэтому необходимо вначале познакомиться с перспективой горизонтально рас­положенного круга.

часть, а у круга, находящегося ниже горизонта,— верхняя. Заметьте, что даже самые узкие эллипсы не имеют изломов на концах большой оси, по­этому при изображении круга в перс­пективе нельзя ограничиваться дуга­ми двух окружностей различных ра­диусов. При таком способе изобра­жения не получается правильной окружности в перспективе. По­смотрите в натуре на эллипс тарел­ки — вы не заметите острых углов, там переход плавный и округлый.

На рис. 9 изображен в перспекти­ве ряд горизонтально расположен­ных окружностей. Окружности в перспективе имеют вид эллипсов. Проследив за их формой, увидим, что по мере приближения к горизон­ту малая ось эллипса уменьшается, и круг, совпадающий с линией гори­зонта, изображается в виде прямой горизонтальной линии. По мере уда­ления круга от линии горизонта ви­димый эллипс будет приближаться по форме к окружности. В этом мож­но легко убедиться, если взять три тарелки, одну из них поставить на пол, другую — на стул, а третью — на стол и отойти на 2—3 метра. Про­мерьте методом визирования (рис. 13) видимые длину и ширину эллипса тарелки на полу, стуле и столе. Чем ниже располагается та­релка, тем более круглый эллипс мы видим; чем ближе к уровню глаз, тем он более сжат, узок. Если поднять тарелку на уровень глаз, то эллипс виден прямой горизонтальной лини- 1г находится т. е. выше нижняя его

 

 

 

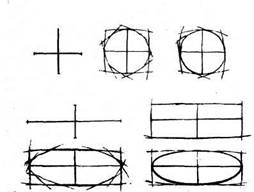
Обратите внимание на малую ось эллипса: дальний ее радиус кажется короче, чем ближний. Это обстоя­тельство необходимо хорошо запом­нить/При рисовании с натуры надо внимательно сравнить длину бли­жайшего к нам отрезка малой оси эллипса с длиной дальнего и выяс­нить, насколько первая длина боль­ше второй.

Каждый начинающий рисоваль­щик должен уметь рисовать окруж­ность и эллипс без помощи чертеж­ных инструментов. На рис. 10 да­на последовательность построения круга и эллипса. Сначала проводят­ся две взаимно перпендикулярные линии — оси симметрии. Через концы их проводятся дуги возможно мень­шей кривизны, затем углы, образо­ванные пересечением дуг, срезаются прямыми линиями. Вновь образовавшиеся углы опять срезаются. В результате нескольких постепен­ных срезов получается круг. Необ­ходимо следить за одинаковой кри­визной по всей окружности.

Эллипс тоже лучше строить по его осям в таком порядке, как это указывалось при построении окруж­ности. При этом необходимо соблю­дать симметрию правой части отно­сительно левой, а также разницу в длине ближней и дальней половин малой оси эллипса.

Рисование цилиндра в верти­кальном и горизонтальном положе­ниях. В начале работы надо опреде­лить положение цилиндра по отно­шению к линии горизонта и его про­порции, т. е. отношение ширины ци-

линдра к высоте. На середине листа проводим вертикальную осевую ли­нию, которая позволит сохранить вертикальное положение цилиндра, а также поможет сделать его симмет­ричным (рис. 11). На этой линии произвольно намечаем высоту ци­линдра, отметив основание и верх­нюю часть предмета. Затем наме­чаем ширину нижнего и верхнего ос­нований цилиндра и боковые верти­кальные стороны его. Далее на гори­зонтальных линиях, проходящих че­рез основания цилиндра, строим большие и малые оси эллипсов. Ве­личина большой оси эллипса равна диаметру оснований цилиндра. Вели­чина малой оси будет зависеть от удаления окружности основания от линии горизонта. Большие оси эл­липсов всегда рисуют под прямым углом к оси цилиндра. Когда разме­ры каждого основания определены, рисуем окружности оснований в виде эллипсов. Боковые стороны у верти­кального цилиндра параллельны вертикальной оси, большие оси эл­липсов оснований равны, а малые оси эллипсов разные, так как верх­нее основание ближе к линии гори­зонта, и эллипс его развернут мень­ше, чем нижний.

Несмотря на то что нижнего ос­нования цилиндра полностью не вид­но, для правильного конструктивного построения и соблюдения симметрии необходимо эллипс нижнего основа­ния рисовать «насквозь».

При рисовании цилиндра в гори­зонтальном и наклонном положени­ях следует помнить, что большие оси эллипса всегда направлены перпен­дикулярно к центральной осевой ли­нии цилиндра, поэтому в первую оче­редь необходимо правильно на­метить направление оси цилиндра на листе бумаги, после чего строить эл­липсы основания.

Так как боковые стороны цилинд­ра направляются в точки схода и ближнее основание развернуто мень­ше дальнего, то эллипсы оснований будут разными как по высоте, так и по щирине. На рис. 12 изображены кувшины в различных положениях: стоя и лежа в разных поворотах. Во всех случаях большие оси эллип­сов оснований перпендикулярны центральной оси кувшина.

При изображении таких сосудов, как показано на рис. 12,а, необходи­мо обращать внимание на то, как у них соединено цилиндрическое гор­лышко с шаровой формой корпуса кувшина. Так как мы смотрим на кувшин несколько сверху, то верхняя цилиндрическая часть закрывает нижнюю шаровую. Надо найти на шаровой форме то место, куда при­соединяется нижняя часть цилиндра. Неопытные рисовальщики, не думая о конструкции предмета, соединя­ют контур шаровой поверхности с нижним основанием цилиндра (рис. 12,6). Такой рисунок не будет объемным. Если закрыть верхнее ос­нование, рисунок будет восприни­маться только как половина кувши­на. Надо следить за тем, чтобы кон­цы большей оси эллипса нижнего основания цилиндра не соединялись с контуром шаровой части кувшина. Чтобы поставить эти две составные части кувшина одну на другую, надо полностью построить шаровую часть, затем, учитывая точки зрения сверху, построить на шаре окруж­ность пересечения с цилиндром. В этом случае концы большой оси эллипса нижнего основания цилинд­рической части не попадут на контур шаровой поверхности. При рисовании предметов ци­линдрической формы иногда встре­чаются трудности в рисовании при­крепленных к ним различных мелких деталей: ручек, горлышек и т. п. Чтобы справиться с такими задача­ми, нужно пользоваться секущими плоскостями. Так, например,

если провести плоскость, проходящую через носик, ручку и воображаемую ось чайника или кастрюли, то линии пересечения этой плоскости со стен­ками сосудов дадут возможность конструктивно точно присоединить эти детали к их боковой форме (рис. 12,в). Такой прием конструк­тивного построения пригодится при рисовании более сложных пред­метов. Построение многогранных призм и пирамид значительно упрощается, если делать построение многоуголь­ников с оснований, вписанных в окружность. Начинать рисовать мно­гоугольник надо с построения перс­пективы окружности, в которую впи­сывается этот многоугольник Это будет эллипс с осями соответствую­щих пропорций. Наблюдая в натуре взаимное расположение вершин уг­лов, засекаем на эллипсе углы мно­гоугольника.

Практические советы. 1. При ри­совании с натуры пропорции пред­метов всегда можно

проверить спо­собом визирования. Делается это так: прижимаем карандаш безымян­ным и средним пальцами к ладони, а большой палец оставляем свобод­ным. Большой палец движется вдоль карандаша и служит для отметки на нем нужного размера (рис.. 13). Ка­рандаш в зависимости от положения измеряемого предмета может накло­няться

и вправо и влево, но при этом он всегда должен быть в вертикаль­ной плоскости, перпендикулярной к лучу зрения. Промеры нужно делать обязательно на предельно вытянутой руке. Без соблюдения этих условий измерения будут ошибочны.

Измерив, например, ширину предмета, переносим карандаш (с отметкой большим пальцем) на вы­соту предмета и сравниваем: во

 

сколько раз ширина укладывается в высоте (или во сколько раз первый предмет больше или меньше друго­го). Это отношение размеров долж­но быть передано на рисунке.

Способом визирования нельзя злоупотреблять, так как он тормо­зит развитие глазомера. Измерения, проводимые на глаз, могут быть точ­нее измерений визирования, если только в результате систематических упражнений хорошо развит глазо­мер.

2. Взаимное расположение пред­метов, движение фигуры, направле­ние любой формы легче определять в натуре и строить на бумаге с по­мощью вертикали и горизонтали.

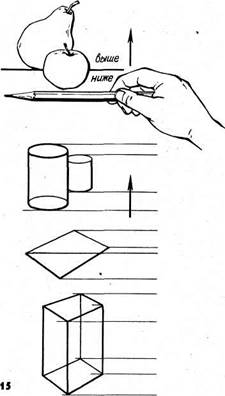
Вертикальные и горизонтальные на­правления чувствуются нами лучше других. По ним легче определить множество других направлений.

Рисуя, например, человеческую фигуру, по вертикально поставлен­ному на вытянутой руке карандашу можно определить положение пятки ноги относительно головы или рук и решить вопрос, находятся ли эти части тела одна над другой или же сдвинуты одна относительно другой (рис. 14).

Выяснение расположения частей предмета относительно горизонтали производится по горизонтально рас­положенному карандашу. Карандаш можно поднимать выше, опускать

ниже и наблюдать, какие части мо­дели располагаются в перспективе ниже других. Таким образом, прове­ряем, уточняем

высоту отдельных то­чек и наклоны линий модели (рис. 15).

 

 

 

Непременным условием правильности проверки является перпенди­кулярное положение карандаша от­носительно луча зрения.

Проверку по вертикали и гори­зонтали полезно проводить только в начальной стадии рисунка. В даль­нейшей работе эта проверка пропор­ций и взаимного расположения пред­метов может осуществляться и дру­гими вспомогательными линиями. С помощью длинного карандаша (спиц или линейки) можно прове­рить правильность построения (перс­пективных углов, пропорций граней, взаимного местоположения предме­тов), если держать его на вытянутой руке вертикально, горизонтально или под углом по направлению перспек­тивы ребер. Например, место­положение основания конуса по от­ношению к ширине верхнего осно­вания куба можно проверить, держа карандаш по вертикали (рис. 43). В натуре эта вертикаль отсека­ет затененную грань куба посере­дине, на нашем рисунке это может оказаться не так. Находим ошибку и исправляем ее. Если продолжить левую сторону конуса (лучше с по­мощью карандаша), она едва кос­нется круглого основания цилиндра, наш рисунок и здесь может быть не­точен. Проводя горизонтальную ли­нию через вазочку, можно опреде­лить ее высоту по отношению к вы­соте конуса. Можно проследить также, куда упрутся обе стороны ци­линдра, если их продолжить. В нату­ре передняя грань куба не совпадает с центром конуса, а на нашем ри­сунке может оказаться в самом центре — так находим еще одну ошибку в своем рисунке. Проведем теперь горизонтально расположен­ный карандаш через основание куба в натуре и посмотрим, насколько ниже пройдет эта линия от основа­ния цилиндра. На нашем рисунке оба эти основания лежат почти на одной горизонтали. В натуре это, возможно, не так. Все, что в натуре дальше,— на рисунке расположено выше, и наоборот.

Светотень. Объемная форма предмета пере­дается на рисунке не только пра­вильным перспективным и конструк­тивным построением, но и свето­тенью. Всякий объемный предмет ограничивается кривыми или плоскими поверхностями, которые при освещении попадают в разные свето­вые условия: лучи света, падая на различные поверхности предметов, освещают их неравномерно. Одни части поверхности получают больше света, другие — меньше. Степень освещенности поверхно­сти предмета изменяется прежде все­го в зависимости от расстояния до источника света: чем дальше от по­верхности находится источник света, тем слабее она освещена, и, наобо­рот, чем ближе находится источник света, тем сильнее освещение. Видимая светлота поверхности предметов зависит также от рас­стояния между предметом и зрите­лем. При удалении освещенные по­верхности постепенно темнеют, а за­темненные — бледнеют (светлеют).

Степень освещенности поверхно­сти зависит и от угла падения лучей света на поверхность. Наиболее сильно освещена та поверхность, на которую лучи падают под прямым углом, т. е. перпендикулярно. Чем больше наклон лучей света к поверх­ности, тем меньше лучей падает на нее и тем слабее она освещена.Светлота предмета зависит от фактуры и цвета самой поверхности:гладкая, полированная поверхность будет больше отражать свет, чем ше­роховатая и матовая. Поверхности темного цвета поглощают больше световых лучей, а отражают меньше. На очень темных и на очень светлых поверхностях светотеневые градации различаются плохо потому, что глаз не способен различать слишком сла­бое и слишком сильное световое раз­дражение.

В качестве наглядного примера распространения светотени на пред­метах в зависимости от угла падения лучей света рассмотрим светотень на простейших геометрических те­лах.