
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность катастрофы ЛА с дублирующими системамиСодержание книги
Поиск на нашем сайте
В этом случае
Перейдем к противоположным событиям и будем иметь:
Вследствие соотношения двойственности из равенства (1.2) получим:
Тогда вероятность катастрофы будет определяться по формуле:
Вследствие независимости событий
Рассмотрим структуру событий ЕKD, ЕKЭ, ЕKC и найдем их вероятности катастроф, связанных с отказом: · двигателей ЕKD; · систем энергоснабжения ЕKЭ; · вспомогательных подсистем ЕKC. Рассмотрим структуру событий Е KD и найдем P(ЕKD) = PKD. Так как событие ЕKD – это событие, состоящее в том, что катастрофа произошла из-за отказа двигателей, а по условию задачи катастрофа, связанная с отказом двигателей, наступает, если выходят из строя любые (r + 1) и более двигателей из m двигателей, а в случае отказа любого r из m двигателей катастрофа наступает с вероятностью PD. Значит,
Так как в нашем случае число двигателей m = 4, а r = 3; то
r + 1 = 3 + 1 = 4. Следовательно,
где ЕKD 3 – событие, состоящее в том, что катастрофа произошла из-за отказа любого r = 3 из m = 4 двигателей; ЕKD ≥4 – событие, состоящее в том, что катастрофа произошла в связи с выходом из строя любых (r+ 1) = 4 и более двигателей, а в нашем случае ЕKD ≥4 = ЕKD 4 – это событие, состоящее в том, что катастрофа произошла из-за отказа всех четырех двигателей. Из этого следует, что
В свою очередь, катастрофа, связанная с отказом r = 3 двигателей (при работающих остальных), не обязательно влечет за собой катастрофу (а с вероятностью PD), значит,
тогда
Так как события ЕKD 3 и ЕKD ≥ 4 несовместны, то
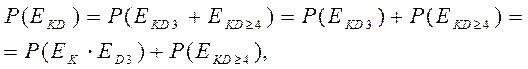
а для нашего случая, учитывая выражение (1.6), получим:
С другой стороны, катастрофа, связанная с отказом r = 3 двигателей (при работающих остальных) из четырех имеющихся у ЛА по условию задачи, есть следующее событие:
то есть работает только 4-й, либо 3-й, либо 2-й, либо 1-й двигатель из четырех имеющихся у ЛА. Доказать, что события EKD 3 и ЕKD ≥ 4 несовместны, можно следующим образом: Согласно равенствам (1.7) и (1.6) имеем:
в соответствии с выражением (1.8) находим далее:
Используя тот факт, что
Но если произведение двух событий равно невозможному событию (пустому множеству), то такие события являются несовместными. ______________________ Примечание –
По определению условной вероятности имеем:
а вследствие независимости событий
Используя равенство (1.7) и несовместимость
Вследствие независимости всех событий
Так как P (Di) = Pi, i = 1,4 и P (EK / ED 3) = PD, то
Если выполняется условие
для всех
а также значит, что
Тогда имеем
(1.10)
Подставив значения, данные из условия задания, получим:
Рассмотрим структуру событий ЕКЭ и найдем Р (ЕКЭ) = РКЭ. ЕКЭ ≡ В 1 · В 2 · В 3– катастрофа, связанная с отказом всех трех систем энергоснабжения (n = 3 по условию задачи). Так как все события В 1 ,
Подставив значения, данные из условия задания, получим
Рассмотрим структуру событий ЕКС и найдем Р (ЕКС) = РКС. Событие ЕКС наступает, если отказывает хотя бы одна из вспомогательных подсистем. Значит,
По закону двойственности
Так как события
Поскольку
Тогда
Если выполняется условие:
то
Подставив значения, данные из условия задания, получим:
Р а с ч е т н а я ч а с т ь
Переходим к числовым расчетам. Вычислим вероятность катастрофы по выведенной нами формуле (1.5). Так как в нашем случае выполняется условие (1.9), то
Если выполняется условие
Видно, что Из этого следует, что вероятность катастрофы, связанной с отказом вспомогательных подсистем, является определяющей.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.38.184 (0.007 с.) |

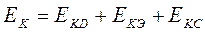 . (1.1)
. (1.1) . (1.2)
. (1.2) . (1.3)
. (1.3) . (1.4)
. (1.4)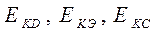 из равенства (1.4) получим:
из равенства (1.4) получим: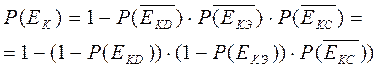
 .
.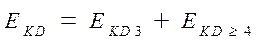 ,
,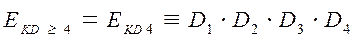 . (1.6)
. (1.6)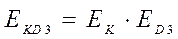 , (1.7)
, (1.7)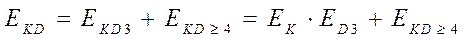 .
.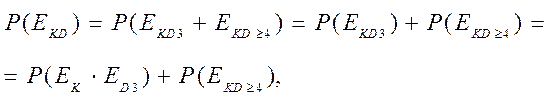
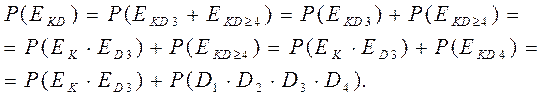
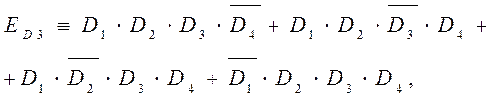
 (1.8)
(1.8)

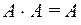 и
и 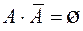 , получим:
, получим:
 и
и  – прерванное и продолженное преобразование текущего выражения.
– прерванное и продолженное преобразование текущего выражения.
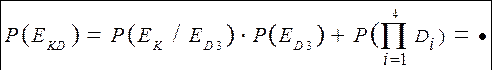
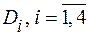 далее находим:
далее находим: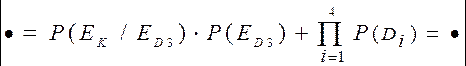
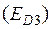 его слагаемых, получим:
его слагаемых, получим: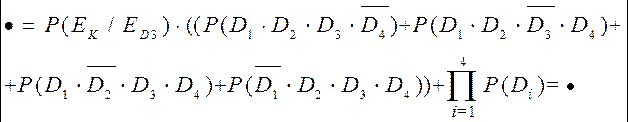
 и так как
и так как  , будем далее иметь:
, будем далее иметь: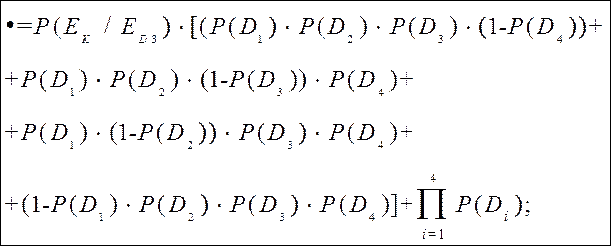
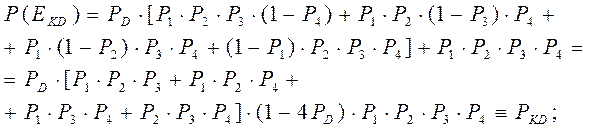
 (1.9)
(1.9) и учитывая, что значение вероятности случайного события меньше единицы, то
и учитывая, что значение вероятности случайного события меньше единицы, то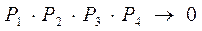 ,
, .
.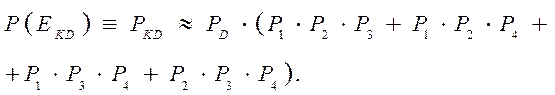

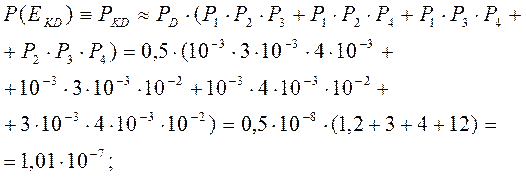 (1.11)
(1.11)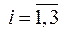 независимы, имеем:
независимы, имеем:
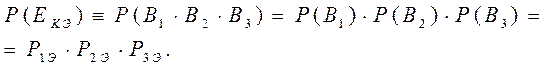 (1.12)
(1.12)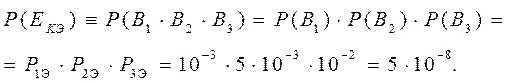
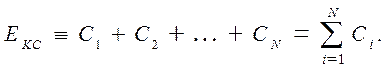

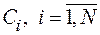 независимы, получим:
независимы, получим: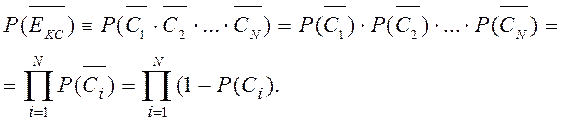
 , получим:
, получим: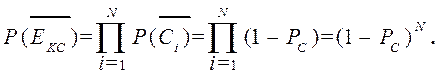


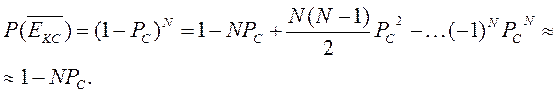
 (1.14)
(1.14)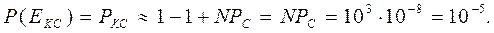 (1.15)
(1.15)
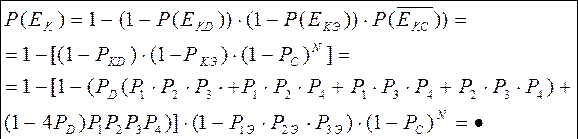
 и
и  и
и 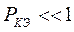 , то будем далее иметь
, то будем далее иметь
 , так как
, так как  .
.


