
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность катастрофы ЛА без дублирующих системСодержание книги
Поиск на нашем сайте
Вероятность катастрофы ЛА без дублирующих систем (один двигатель с вероятностью катастрофы
где
Исходя из исходных данных будем иметь:
а как уже подсчитано ранее,
Так как
то из этого следует, что вероятность катастрофы, связанной с отказом двигателя и систем энергоснабжения, является определяющей.
И, наконец, сравним вероятности
В ы в о д Наиболее вероятной является катастрофа, связанная с отказом одной из вспомогательных подсистем, а отсутствие дублирующих систем увеличивает вероятность катастрофы в 199 раз, при этом определяющим фактором становится отказ двигателя или системы энергоснабжения.
1.3 Варианты задания 1 Числовые данные, соответствующие вариантам задания, приведены в таблице 1, а варианты задания выбираются из приложения А в соответствии с порядковым номером курсанта в списке группы журнала учета учебных занятий.
_______________________ Примечание – При оформлении решения задачи следует использовать формулировки и тождества используемых теорем.
Окончание таблицы 1
Задание 2 ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СИСТЕМЫ ЭНЕРГОСНАБЖЕНИЯ САМОЛЕТА Задача Испытываются m элементов системы энергоснабжения самолета, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону с функциями распределения Определить вероятность того, что в интервале (0; · только один элемент; · только два элемента; ………………………… · все m элементов; · ни один из m элементов не откажет. 2.2 Типовой пример решения задачи Дано:
Решение М а т е м а т и ч е с к а я ч а с т ь
Введем обозначения:
Тогда
Так как время безотказной работы элемента определяется его функцией надежности, которая равна
вероятность безотказной работы i -го элемента будет
Таким образом, вероятность безотказной работы 1-го элемента в заданном интервале (0; 5) будет
Вероятность отказа 1-го элемента в заданном интервале (0; 5) будет
_________________________ Примечание – Значения функции у = е-х взяты из приложения Б.
Вероятность безотказной работы 2-го элемента в заданном интервале (0; 5) будет
Вероятность отказа 2-го элемента в заданном интервале (0; 5) будет
Вероятность безотказной работы 3-го элемента в заданном интервале (0; 5) будет
Вероятность отказа 3-го элемента в заданном интервале (0; 5) будет
Р а с ч е т н а я ч а с т ь Переходим к расчету искомых вероятностей, которые находятся следующим образом: Вероятность отказа только одного элемента в заданном интервале (0; 5) будет
вероятность отказа только двух элементов в заданном интервале (0; 5) будет
вероятность отказа всех трех элементов в заданном интервале (0; 5) будет
вероятность безотказной работы всех трех элементов во время испытаний в заданном интервале (0; 5) будет
В ы в о д При заданных данных во время испытаний в заданном интервале (0; 5) наиболее вероятным является отказ только двух элементов, а наименее вероятным – отказ всех трех элементов, так как
Вероятность же того, что все три элемента безотказно отработают во время испытаний в заданном интервале (0; 5) является небольшой, а именно
2. 3 Варианты задания 2 Числовые данные, соответствующие вариантам задания 2, приведены в таблице 2, а варианты задания выбираются из приложения А в соответствии с порядковым номером курсанта в списке группы журнала учета учебных занятий. Таблица 2 – Числовые данные, соответствующие вариантам задания 2
Окончание таблицы 2
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.114.8 (0.011 с.) |

 , одна система энергоснабжения с вероятностью отказа
, одна система энергоснабжения с вероятностью отказа  и N вспомогательных подсистем с вероятностью отказа
и N вспомогательных подсистем с вероятностью отказа 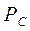 каждая) с учетом, что все упомянутые выше системы и подсистемы ЛА функционируют независимо друг от друга, будет определяться по формуле:
каждая) с учетом, что все упомянутые выше системы и подсистемы ЛА функционируют независимо друг от друга, будет определяться по формуле: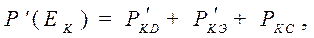 (1.16)
(1.16)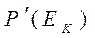 – вероятность катастрофы ЛА без дублирующих систем;
– вероятность катастрофы ЛА без дублирующих систем;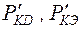 – вероятность катастрофы, связанной с отказом двигателя, системы энергоснабжения соответственно в случае без дублирующих систем.
– вероятность катастрофы, связанной с отказом двигателя, системы энергоснабжения соответственно в случае без дублирующих систем.
 , то, подставив эти значения в формулу (1.16), получим:
, то, подставив эти значения в формулу (1.16), получим: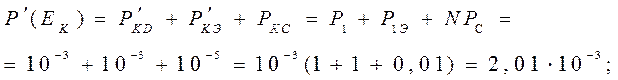
 ≫
≫ 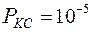 ,
, и
и 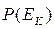 :
:
 Таблица 1 – Числовые данные, соответствующие вариантам задания 1
Таблица 1 – Числовые данные, соответствующие вариантам задания 1
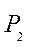
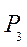






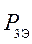




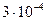
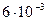



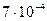


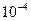









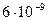
 20
20
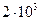


 для каждого из m элементов.
для каждого из m элементов. ) часов откажут:
) часов откажут:

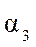
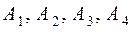 – события, состоящие в том, что отказал только один элемент, только два, все три элемента, ни один элемент не отказал;
– события, состоящие в том, что отказал только один элемент, только два, все три элемента, ни один элемент не отказал;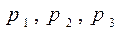 – вероятности отказа 1-го, 2-го, 3-го элемента в заданном интервале (0; 5) соответственно.
– вероятности отказа 1-го, 2-го, 3-го элемента в заданном интервале (0; 5) соответственно. – вероятности безотказной работы 1-го, 2-го, 3-го элемента в заданном интервале (0; 5) соответственно.
– вероятности безотказной работы 1-го, 2-го, 3-го элемента в заданном интервале (0; 5) соответственно.
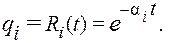


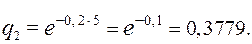

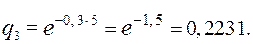
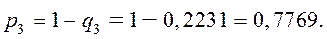


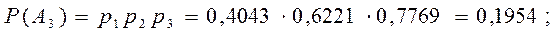

 .
.






