
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как определяется степень кинематической неопределимости рам?Содержание книги
Поиск на нашем сайте
Число независимых линейных смещений узлов системы равно числу стержней, которые необходимо ввести в шарнирную схему сооружения, чтобы превратить ее в геометрически неизменяемую. Следовательно, число независимых линейных смещений узлов равно степени геометрической изменяемости системы, полученной из заданной путем введения во все «жесткие» узлы полных шарниров.
В качестве примера рассмотрим первую раму. Число «жестких» узлов этой рамы равно двум, т.е. ny =2. Для определения числа неизвестных линейных смещений переходим к шарнирной схеме (второй рисунок), представляющую собой изменяемую систему; для превращения ее в геометрически неизменяемую достаточно поставить один стержень, например опорный CE (рисунок третий) или диагональный AC (рис. 4). На втором рисунке штриховой линией показаны возможные перемещения сторон шарнирного четырехугольника; из рассмотрения этого рисунка видно, что шарниры В и С не могут перемещаться независимо друг от друга. Итак, число независимых линейных перемещений в данном случае равно единице, т.е. nл =1; Как определяется число угловых смещений узлов в методе перемещений?
Как определяется число линейных смещений. nл кол-во возможных линейных смещений жёстких и шарнирных узлов системы, определяется по кл-ву линейных смещений вертикальных и горизонтальных стержней и шарнирных узлов.
Кононические уравнения метода перемещений, их хар-ка и физ-ий смысл. Основная система метода перемещений должна работать и деформироваться также как и заданная. Для удовлетворения этого условия необходимо чтобы все реактивные усилия возникающие в фективных связях от единичных смещений и от единичной нагрузки были равны 0. Аналитическая запись этих условий и представляет собой кононическое уравнение метода перемещений: r11z1+r12z2+…+r1nzn+R1p=0, r ik реактивное усилие(момент, силы) возникающие в i-ой r21z1+r22z2+…+r2nzn+R2p=0 дополнительной связи фективной заделки линейной связи от единичного смещения в k-ой дополнительной связи. R ip реактивное rn1z1+rn2z2+…+rnnzn+Rnp=0 усилие возникающее в i-ой дополнительной связи (фективной заделки линейной связи) от действия внешней нагрузки. Физический смысл ур-я: Реактивное усилие возникающие в i-ой дополнительной связи фективной заделки от единичных смещений во всех остальных дополнительных связях и от внешней нагрузки=0 Определите для представленной рамы степень кинематической неопределимости и изобразить основную систему метода перемещений.
Л = -W, Л – это число лишних связей. 1) Л=3К-Ш 2) Л=-(3D-2Ш-Co) 3) Для фермы Л=(-2y-C-Co) 4) Для систем, состоящих из одного диска Л=Ш-3
Основная система метода перемещений её хар-ка и смысл При расчёте методом перемещений сис. расчленяется на ряд однопролётных статич. неопр. балок. Это достигается введением в неё дополнит. связей.В осн. сис. метода перемещений во всех жёстких узлах устанавливают дополнит. фиктивные заделки;по направлению возможных линейных смещений устанавлив. дополнит. линейные связи.Св-ва фиктивной заделки: она препятствует повороту и не препят. линейным смещениям. Анализ осн. сис. метода перемещ. показывает, что она состоит из совокупности простых балок, имеющих жёсткое и шарнирное опирание, и явл. статич. неопр.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.200 (0.005 с.) |

 Число неизвестных углов поворота равно числу «жестких» узлов, а потому определение ny сводится к простому подсчету числа «жестких» узлов рамы. «Жестким» считается такой узел, в котором концы, по крайней мере, двух из сходящихся в нем стержней жестко связаны между собой.
Число неизвестных углов поворота равно числу «жестких» узлов, а потому определение ny сводится к простому подсчету числа «жестких» узлов рамы. «Жестким» считается такой узел, в котором концы, по крайней мере, двух из сходящихся в нем стержней жестко связаны между собой.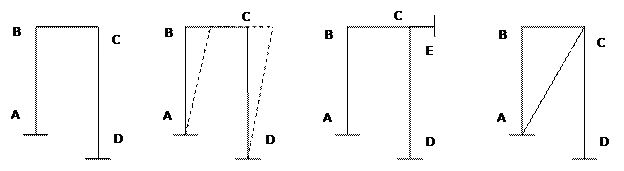

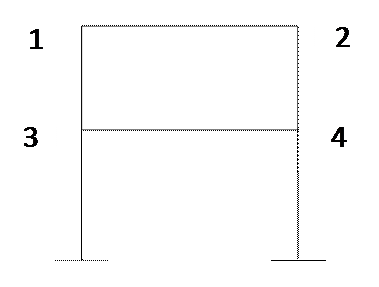 Для определения числа условных смещений узлов необходимо знать число «жестких» узлов.. «Жестким» считается такой узел, в котором концы, по крайней мере, двух из сходящихся в нем стержней жестко связаны между собой. (например узлы 1, 2, 3, 4).
Для определения числа условных смещений узлов необходимо знать число «жестких» узлов.. «Жестким» считается такой узел, в котором концы, по крайней мере, двух из сходящихся в нем стержней жестко связаны между собой. (например узлы 1, 2, 3, 4). Если стержни, сходящиеся в каком-либо узле системы, соединены в несколько жестких групп, шарнирно связанных между собой, то такой узел имеет количество «жестких» узлов, равное числу групп (например узел 1)
Если стержни, сходящиеся в каком-либо узле системы, соединены в несколько жестких групп, шарнирно связанных между собой, то такой узел имеет количество «жестких» узлов, равное числу групп (например узел 1)


