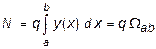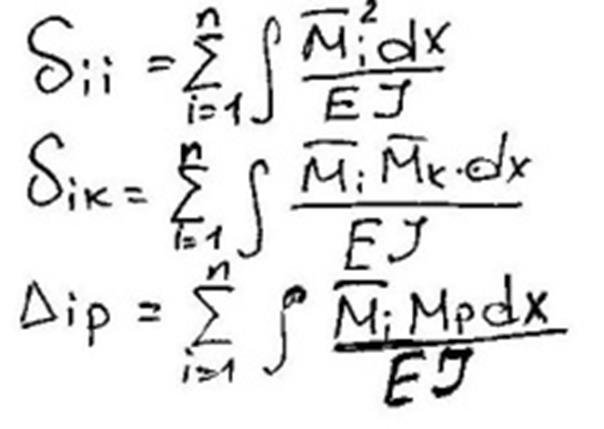Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчётная схема сооружения, проблемы её выбора.Содержание книги
Поиск на нашем сайте
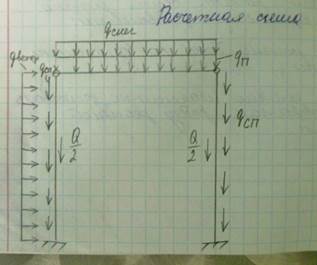
Расчётная схема сооружения, проблемы её выбора. Расчётная схема сооружения – это упрощенная идеализированная схема, которая учитывает все параметры реальной схемы сооружения и не учитывает не существенные параметры. Выбор расчётной схемы сооружений является очень важным этапом расчёта. При этом расчётная схема должна удовлетворять следующим требованиям: 1)она должна быть по возможности простой;2)она должна максимально учитывать и отображать работу реальной схемы. К-колонна, СП – стеновая панель, ПБ – подкрановая балка, ПП – панель покрытия, ФП – ферма покрытия
2. Виды опор и их свойства.
отображение на расчетной схеме - количество связей – 1, количество степеней свободы – 2, количество реакций – 1.
отображение на расчетной схеме - количество связей – 2, количество степеней свободы – 1, количество реакций – 2.
отображение на расчетной схеме - количество связей – 3, количество степеней свободы – 0, количество реакций – 3.
отображение на расчетной схеме -
количество связей – 2, количество степеней свободы – 1, количество реакций – 2. Основные гипотезы и принципы, положенные в основу классических Методов расчета строительной механики. В строительной механике используют такие методы как аналитические, графические и графоаналитические. Аналитические: статический метод – использование уравнений статического равновесия Σx=0; Σy=0; ΣM=0. Этот метод включает такой способ как способ вырезания узлов, простых сечений и их комбинаций. Метод замены стержней состоит в том что заданную систему заменяют более простой путём перестановки стержней. Перестановка должна быть такой чтобы новая система оставалась геометрически не изменяемой, поддавалась простым расчетам. В основу кинематического метода положен метод возможных перемещений(в системе удаляется та связь, реакцию которой необходимо определить), который основывается на ряде принципов: понятие об идеально упругом теле; элементы сооружений при деформировании подчиняется закону Гука, который имеет зависимость между перемещениями и нагрузкой: Δ=αР, α – коэффициент пропорциональности, Р – нагрузка, Δ – перемещение; считают приложение нагрузки статически; при расчетах используют принцип независимости действия сил, т.е. результат действия нескольких сил на систему равен сумме результатов каждой силы в отдельности.
Внутрение усилия в плоских стержневых системах, их вычисления. Расчёт систем методам строительной механики заключается в определении внутренних усилий. Порядок расчёта: 1)определение опорных реакций: т.к. рама на плоскости является диском, то для определения опорных реакций необходимо составить три уравнения равновесия: Σx=0; Σy=0; ΣM=0. При этом: 2) раму разбивают на простые участки, на которых жесткость элементов постоянно и закон распространения эпюр в этих усилиях известен
Для определение внутренних усилий используют метод сечений. Суть которого заключается в рассечении рамы на две части и рассмотрении равновесия одной из отсечённых частей. При этом внутренние усилия в искомом сечении представляют как внешнюю нагрузку действующую от отсечённой части. Момент сечений возникает в плоскости, перпендикулярной плоскости сечения; 4) нахождение внутренних усилий. Изгибающий момент в сечении равен сумме моментов от всех внешних нагрузок, включая опорные реакции, приложенных к одной части рамы от сечения и взятых относительно центра тяжести данной системы. Поперечная сила равна сумме проекций всех сил, приложенных к одной части рамы от сечения на ось, перпендикулярной к оси стержня, на которой находится сечение. Продольная сила равна сумме проекций всех сил, приложенных к одной части рамы от сечения на ось, параллельную к оси стержня: q=dQ/dx; Q=dM/dx, dM=Q*dx. Из дифференциальной зависимости вытекают следствия о взаимодействии эпюр внутренних усилий. Определения усилий по линиям влияния от внешних нагрузок. По линиям влияния можно находить ycилие, дейcтвyющее в данном cечении. Еcли нагpyзка пpедcтавляет cобой cиcтемy cоcpедоточенных гpyзов P1, P2, P3,..., Pn (рис.), то ycилие:
Для pавномеpно pаcпpеделенной нагpyзки (рис.) q = const:
где ab - площадь, огpаниченная линией влияния, оcью абcциcc и пpямыми x = a и x = b, a и b - кооpдинаты начальной и конечной точек дейcтвия pаcпpеделенной нагpyзки.
Запишите ф-лу Мора
δii - главные 1-ые коэф канонических уравнений δik- вторичные коэфициенты Δip- грузовые коэфициенты Мi-эпюра изгибающих моментов от действия единичной нагрузки Мр-эпюра изгибающих моментов от действия внешней нагрузки ЕЈ-жёсткость сечения стержня в плоскости изгиба n-число участков.
Расчётная схема сооружения, проблемы её выбора. Расчётная схема сооружения – это упрощенная идеализированная схема, которая учитывает все параметры реальной схемы сооружения и не учитывает не существенные параметры. Выбор расчётной схемы сооружений является очень важным этапом расчёта. При этом расчётная схема должна удовлетворять следующим требованиям: 1)она должна быть по возможности простой;2)она должна максимально учитывать и отображать работу реальной схемы. К-колонна, СП – стеновая панель, ПБ – подкрановая балка, ПП – панель покрытия, ФП – ферма покрытия
2. Виды опор и их свойства.
отображение на расчетной схеме - количество связей – 1, количество степеней свободы – 2, количество реакций – 1.
отображение на расчетной схеме - количество связей – 2, количество степеней свободы – 1, количество реакций – 2.
отображение на расчетной схеме - количество связей – 3, количество степеней свободы – 0, количество реакций – 3.
отображение на расчетной схеме -
количество связей – 2, количество степеней свободы – 1, количество реакций – 2.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.67 (0.008 с.) |


 Шарнирно подвижная:
Шарнирно подвижная:
 Шарнирно не подвижная:
Шарнирно не подвижная:
 Жесткая заделка:
Жесткая заделка:
 Плавающая заделка:
Плавающая заделка:
 3) определение ординат внутренних усилий и построение эпюр внутренних усилий.
3) определение ординат внутренних усилий и построение эпюр внутренних усилий.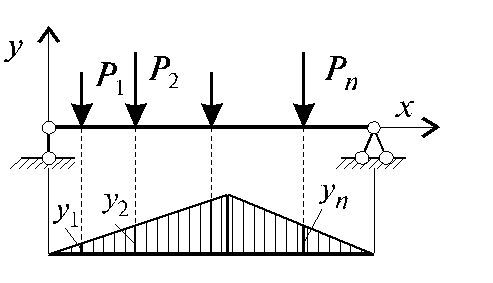
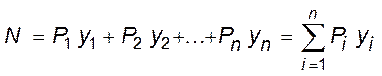 yi - оpдинаты линий влияния под гpyзами Pi (i = 1,2,3,...,n).
yi - оpдинаты линий влияния под гpyзами Pi (i = 1,2,3,...,n).