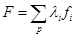Основные показатели качества покрытия

Оптимизация покрытия производится по таким показателям:

n суммарная стоимость модулей, участвующих в покрытии;

n общее число модулей;

n число типов используемых модулей;

n количество связей между модулями;

n количество неиспользуемых логических элементов в модуле.

 

Возможные математические формулировки задачи покрытия

Пусть задан набор модулей T = (t ₁, t ₂,... t_n), где n – число типов модулей в наборе. Такой набор характеризуется матрицей

 

где a_ij – соответствует числу логических элементов i -го типа в модуле j -го типа, m – общее число типов логических элементов во всех модулях набора.

Поэлементный состав заданной функциональной схемы характеризуется вектором

В=(в1,в2,…ві)

где b_i – число логических элементов i -го типа в схеме.

Введем целочисленную переменную x_j, характеризующую количества модулей j -го типа, необходимых для покрытия заданной схемы.

В простейшем случае, когда ставится задача покрытия с минимальным количеством модулей, целевая функция принимает вид:

 

При ограничениях:

, i = 1, 2,..., m; x_j ³ 0; j = 1,2,..., n; a_ij >0.

При минимизации стоимости:

где c_j – стоимость модуля j -го типа.

В случае учета нескольких требований вводится дополнительные критерии, например, при учете критериев стоимости и количества модулей

 

где k ₁ и k ₂ – коэффициенты важности критериев.

 

 

Задача разбиения

Исходными данными задачи является схема соединений конструктивных элементов.

Задача состоит в необходимости разделить исходную схему на части так, чтобы образовать конструктивные узлы следующего иерархического уровня с учетом требований и ограничений.

Качество выполнения задачи разбиения анализируется по таким критериям:

n длина внешних связей;

n объем конструкции, характеризуемый числом узлов разбиения;

n числом различных типов узлов;

n неразрывность функциональных назначений узлов.

Исходную схему соединения элементов можно представить взвешенным мульти графом

G = (X, A),

в котором элементы – вершины узла, а межэлементные связи – ребра.

Пусть заданы ограничения на вместимость узлов – k и допустимое число внешних выводов в узле – v. Требуется разрезать исходный граф на отдельные подграфы

G _l = (X _l, A _l),

где l – число подграфов (1, 2,..., m).

Выделяем три узла G1, G2, G3 получаем граф G¢ = (X ¢, A ¢) где множество вершин X¢ – соответствует узлам разбиения, а множество ребер A ¢ определяет межузловые соединения.

 

 

Задача размещения

Исходные данные:

n схема соединений конструктивных элементов узла;

n конструктивные параметры элементов;

n параметры монтажного пространства.

Решение задачи заключается в определении оптимального расположения элементов в заданном монтажном пространстве с учетом требований и ограничений.

Главная задачи размещения – облегчение следующего за ней процесса трассировки соединений.

При проводном монтаже главный критерий оптимальности есть суммарная взвешенная длина соединений

Для печатного монтажа помимо этого имеет значение взаимное расположение соединений и число пересечений, что учитывается дополнительным критерием суммарной длины кратчайших деревьев.

Формализация задачи размещения характерна для случая регулярного пространства и одинаковых элементов.

За основу возьмем граф G = (X, A), который характеризуется матрицей смежности

 

где n – число модулей; a_ij –число соединений между модулями x_i и x_j.

Разобьем площадь реальной печатной платы в координатах X, Y на m областей (позиций)

Поставим в соответствие печатной плате граф G _r =(P, U) где множество вершин – центры посадочных мест, множество ребер – координатная решетка, связывающая вершины графа.

Граф G _r характеризуется матрицей расстояний

D =[ d_ij ] m´m,

где d_ij – расстояние между позициями i и j.

Введем матрицу назначений, характеризующую результаты решения задачи размещения:

B =[ b_ij ] n´m,

где b_ij = 1, если x_i находится в позиции p_j и b_ij =0 в противном случае.

Тогда суммарная взвешенная длина соединений при произвольном размещении модулей будет

 

 

Задача состоит в минимизации функционала F при изменяемой матрице B и ограничениях

 

 

Задача трассировки

Задача трассировки формулируется следующим образом:

По заданной схеме соединений проложить необходимые проводники на плоскости (плате), чтобы реализовать заданные технические соединения с учетом заранее заданных ограничений.

Основные ограничения:

n Ширина проводников;

n Минимальные расстояния между ними.

Исходная информация:

n список цепей,

n параметры конструкции элементов и коммутационного поля,

n данные по размещению элементов.

Критерии трассировки:

n процент реализованных соединений,

n суммарная длина проводников,

n число пересечений проводников,

n число монтажных слоев,

n число межслойных переходов,

n равномерность распределения проводников,

n минимальная область трассировки и т.д.

Оценка качества трассировки ведется по доминирующему критерию при выполнении ограничений по другим критериям либо с применением аддитивной или мультипликативнай формы оценочной функции, например следующего вида

 

где F – аддитивный критерий; λ_i – весовой коэффициент; f_i – частный критерий; p – число частных критериев