
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Третий закон Кеплера (гармонический закон)Содержание книги Поиск на нашем сайте
Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.
Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды. №10 В 1604 году Кеплер публикует свои наблюдения сверхновой, называемой теперь его именем. Будучи великолепным наблюдателем, Тихо Браге за много лет составил объёмный труд по наблюдению планет и сотен звёзд, причём точность его измерений была существенно выше, чем у всех предшественников. Для повышения точности Браге применял как технические усовершенствования, так и специальную методику нейтрализации погрешностей наблюдения. Особо ценной была систематичность измерений. На протяжении нескольких лет Кеплер внимательно изучает данные Браге и в результате тщательного анализа приходит к выводу, что траектория движения Марса представляет собой не круг, а эллипс, в одном из фокусов которого находится Солнце — положение, известное сегодня как первый закон Кеплера. Дальнейший анализ привёл ко второму закону: радиус-вектор, соединяющий планету и Солнце, в равное время описывает равные площади. Это означало, что чем дальше планета от Солнца, тем медленнее она движется. Оба закона были сформулированы Кеплером в 1609 году в книге «Новая астрономия», причём, осторожности ради, он относил их только к Марсу. №11 В 1609 году Галилей самостоятельно построил свой первый телескоп с выпуклым объективом и вогнутым окуляром. Труба давала приблизительно трёхкратное увеличение[85]. Вскоре ему удалось построить телескоп, дающий увеличение в 32 раза. Отметим, что термин телескоп ввёл в науку именно Галилей (сам термин предложил ему Федерико Чези, основатель «Академии деи Линчеи»).[86] Ряд телескопических открытий Галилея способствовали утверждению гелиоцентрической системы мира, которую Галилей активно пропагандировал, и опровержению взглядов геоцентристов Аристотеля и Птолемея. Первые телескопические наблюдения небесных тел Галилей провёл 7 января 1610 года.[1][87] Эти наблюдения показали, что Луна, подобно Земле, имеет сложный рельеф — покрыта горами и кратерами. Известный с древних времен пепельный свет Луны Галилей объяснил как результат попадания на наш естественный спутник солнечного света, отражённого Землёй. Галилей открыл также (независимо от Иоганна Фабрициуса и Хэрриота) солнечные пятна. Существование пятен и их постоянная изменчивость опровергали тезис Аристотеля о совершенстве небес (в отличие от «подлунного мира»). [31] По результатам их наблюдений Галилей сделал вывод, что Солнце вращается вокруг своей оси, оценил период этого вращения и положение оси Солнца. 12???? №13 Находясь в Падуанском университете, Галилей изучал инерцию и свободное падение тел. В частности, он заметил, что ускорение свободного падения не зависит от веса тела, таким образом опровергнув первое утверждение Аристотеля. В своей последней книге Галилей сформулировал правильные законы падения: скорость нарастает пропорционально времени, а путь — пропорционально квадрату времени.[76] В соответствии со своим научным методом он тут же привёл опытные данные, подтверждающие открытые им законы. Более того, Галилей рассмотрел (в 4-й день «Бесед») и обобщённую задачу: исследовать поведение падающего тела с ненулевой горизонтальной начальной скоростью. Он совершенно правильно предположил, что полёт такого тела будет представлять собой суперпозицию(наложение) двух «простых движений»: равномерного горизонтального движения по инерции и равноускоренного вертикального падения. Галилей доказал, что указанное, а также любое брошенное под углом к горизонту тело летит по параболе.[76] В истории науки это первая решённая задачадинамики. В заключение исследования Галилей доказал, что максимальная дальность полёта брошенного тела достигается для угла броска 45° (ранее это предположение высказал Тарталья, который, однако, не смог его строго обосновать[77]). На основе своей модели Галилей (ещё в Венеции) составил первые артиллерийские таблицы.[78] Галилей опроверг и второй из приведённых законов Аристотеля, сформулировав первый закон механики (закон инерции): при отсутствии внешних сил тело либо покоится, либо равномерно движется. То, что мы называем инерцией, Галилей поэтически назвал «неистребимо запечатлённое движение». Правда, он допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Правильную формулировку закона позднее дали Декарт и Ньютон; тем не менее общепризнанно, что само понятие «движение по инерции» впервые введено Галилеем, и первый закон механики по справедливости носит его имя.[79] №14 При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения. Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта. [1] Различают принцип относительности Эйнштейна (который приведён выше) и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.129.141 (0.006 с.) |

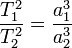 , где T 1 и T 2 — периоды обращения двух планет вокруг Солнца, а a 1 и a 2 — длины больших полуосей их орбит.
, где T 1 и T 2 — периоды обращения двух планет вокруг Солнца, а a 1 и a 2 — длины больших полуосей их орбит. , где M — масса Солнца, а m 1 и m 2 — массы планет.
, где M — масса Солнца, а m 1 и m 2 — массы планет.


