
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор оптимальных параметров настройки типовых регуляторовСодержание книги
Поиск на нашем сайте
Выбор оптимальных параметров настройки типовых регуляторов Под законом регулирования понимают уравнения связи между управляющим воздействием и величиной ошибки. Оптимальный закон регулирования можно выбрать исходя из следующих соображений:
Необходимо достичь Поэтому можно приближенно принять:
При разложении в ряд Фурье
Оптимальная передаточная функция системы в разомкнутом состоянии должна быть эквивалентна интегральному звену, что обеспечит всегда монотонный переходный процесс в системе, т.к. в замкнутом состоянии система – апериодическое звено.
Для линейных законов регулирования параметры настройки можно выбирать с использованием ЛАЧХ. Для этого строят ЛАЧХ ОУ и желаемую ЛАЧХ; вычитая затем из ЛАЧХ желаемой ЛАЧХ ОУ, определяют структуру и параметры регулятора. Можно не строить желаемую ЛАЧХ, а, построив ЛАЧХ ОУ и выбранного ориентировочного регулятора, совмещая их, получить желаемую ЛАЧХ выбирая параметры регулятора [ метод полной компенсации постоянных времени объекта ]
Выбор оптимальных параметров настройки регулятора на основании интегральных оценок качества
Можно использовать интегральную оценку (квадратичная простая):
Если на входе
Сложность использования
Для определения оптимальных параметров настройки регулятора нужно найти минимальное значение интеграла.
Квадратичная простая оценка
Это интеграл вычислен и существует в таблицах Мак-Ленона, которые позволяют по коэффициентам полиномов
Для определения минимального значения интеграла
Выбор оптимальных параметров настройки регулятора на основании критерия «максимальной степени устойчивости»
Под критерием степенью устойчивости ( При выборе параметров регулятора на основании критерия задаются степенью устойчивости, которая характеризует:
Если ближайшим к мнимой оси является вещественный корень, а остальные комплексные, но расположены дальше, то переходный процесс с перерегулированием не более 20%. Характеристическое уравнение запишется т.о., чтобы выделить коэффициенты:
Это уравнение дифференцируют n раз и составляют систему уравнений, на основании которой и определяют оптимальные параметры настойки регулятора.
Настройка регуляторов на симметричный оптимум При такой настройке ЛАЧХ желаемой системы имеет астатизм 2-го порядка, время первого достижения выходной величиной установившегося значения составляет
Оптимальные САУ. Критерии оптимальности и ограничения. Критерии оптимизации В качестве критерия оптимизации могут выбираться различные экономические и технико-экономические параметры. При оптимизации статики и установившихся режимов работы многомерных объектов критерии оптимизации формулируются как некоторая функция, характеризующая качество работы объекта.
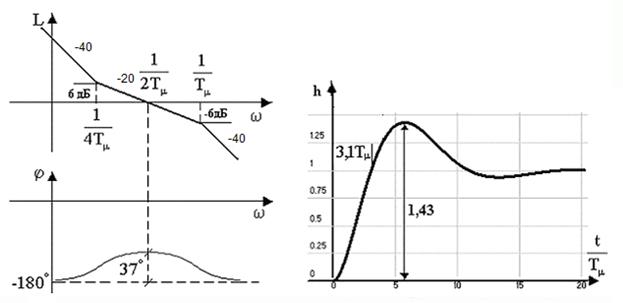
В качестве критерия оптимизации (на высших уровнях АСУТП) может применяться ф-ция пользы, которая представляет собой некоторую сумму: 1) X – вектор координат состояний объекта Y – вектор выходных состояний объекта U – вектор управляющих воздействий 2) максимум прибыли
g – цена П – производительность S – затраты
3) минимум потерь
Xi(t) – реализуемая переменная технологического процесса Si – стоимость потерь от нестабильности i-ой переменной Во многих случаях качество работы АСУТП оценивается несколькими критериями, часть из которых противоречива. Тогда либо формируют векторный критерий либо используют один показатель качества, а на остальные накладывают ограничения. Векторный критерий оптимизации: От векторного критерия переходят к обобщенному скалярному:
Сi – коэффициент, отражающий вклад частного критерия в общий скалярный
Наиболее распространенными критериями оптимизации на уровне САР являются: 1) обеспечение максимального быстродействия
2) максимальная точность
При использовании в качестве функционала этого критерия в системе возникают процессы с большим перерегулированием 3) λ – коэффициент, ограничивающий скорость переходного процесса, т.е. величину перерегулирования. 4) для стохастических систем в качестве критерия оптимизации можно использовать среднее значение квадрата ошибки
5) расход энергии на управление
6) если используются механические источники энергии
U(t) – управляющее воздействие
7) если на объект управления действуют возмущения (контролируемые и неконтролируемые), то в качестве критерия принят функционал, характеризующий взаимную корреляцию между выходом и возмущением:
В общей постановке задачи оптимизации минимизируемый функционал детерминированных систем можно записать в следующем виде:
F – подынтегральная функция функционала качества (характеризует динамику).
Выбор оптимальных параметров настройки типовых регуляторов Под законом регулирования понимают уравнения связи между управляющим воздействием и величиной ошибки. Оптимальный закон регулирования можно выбрать исходя из следующих соображений:
Необходимо достичь Поэтому можно приближенно принять:
При разложении в ряд Фурье
Оптимальная передаточная функция системы в разомкнутом состоянии должна быть эквивалентна интегральному звену, что обеспечит всегда монотонный переходный процесс в системе, т.к. в замкнутом состоянии система – апериодическое звено.
Для линейных законов регулирования параметры настройки можно выбирать с использованием ЛАЧХ. Для этого строят ЛАЧХ ОУ и желаемую ЛАЧХ; вычитая затем из ЛАЧХ желаемой ЛАЧХ ОУ, определяют структуру и параметры регулятора. Можно не строить желаемую ЛАЧХ, а, построив ЛАЧХ ОУ и выбранного ориентировочного регулятора, совмещая их, получить желаемую ЛАЧХ выбирая параметры регулятора [ метод полной компенсации постоянных времени объекта ]
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.007 с.) |


 . Для этого необходимо
. Для этого необходимо  , что практически не выполнимо, т.к. для этого необходимо, чтобы коэффициент преобразования системы во всем диапазоне частот был постоянным.
, что практически не выполнимо, т.к. для этого необходимо, чтобы коэффициент преобразования системы во всем диапазоне частот был постоянным. и для диапазона частот, где
и для диапазона частот, где  ,
,  .
.

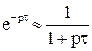
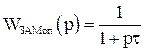 - оптимальная передаточная функция системы в замкнутом состоянии.
- оптимальная передаточная функция системы в замкнутом состоянии.




 (квадратичная)
(квадратичная)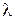 – коэффициент, ограничивающий скорость переходного процесса, т.е. величину перерегулирования.
– коэффициент, ограничивающий скорость переходного процесса, т.е. величину перерегулирования. связана с тем, что нужно правильно выбрать
связана с тем, что нужно правильно выбрать  .
. вычисляется по формуле Релея:
вычисляется по формуле Релея:
 – амплитудный спектр сигнала ошибки.
– амплитудный спектр сигнала ошибки.
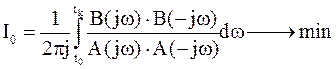
 и
и  вычислять значения интеграла.
вычислять значения интеграла.

 ) понимают расстояние ближайшего корня до мнимой оси.
) понимают расстояние ближайшего корня до мнимой оси.
 , где
, где 
 – не содержит параметра регулятора
– не содержит параметра регулятора – содержит параметр регулятора
– содержит параметр регулятора
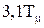 , максимальное перерегулирование достигает 43%, запас по фазе 37° но при этом в системе переходной процесс с перерегулированием до 40% и выше.
, максимальное перерегулирование достигает 43%, запас по фазе 37° но при этом в системе переходной процесс с перерегулированием до 40% и выше.

 à max
à max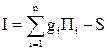 à max
à max à min
à min


 à min
à min à min
à min à min
à min à min
à min à min
à min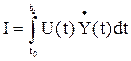 à min
à min – скорость изменения выходного сигнала
– скорость изменения выходного сигнала à min
à min à min
à min – функция, характеризующая качество в конечный момент времени, т.е. после завершения переходного процесса.
– функция, характеризующая качество в конечный момент времени, т.е. после завершения переходного процесса.


