
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод классического вариационного исчисленияСодержание книги
Поиск на нашем сайте
Оптимальные САУ разрабатываются для сложных объектов с многими регулируемыми параметрами. Состояние объекта управления в процессе управления можно охарактеризовать некоторыми функциями времени
Информация о текущем состоянии объекта содержится в контролируемых выходных переменных
На объект действуют также внешние и внутренние возмущения:
Для достижения желательного качества объекта к нему необходимо приложить управляющее воздействие:
Цель управления может быть задана различными способами. Чаще в виде допустимого значения некоторого функционала I, который называется целевой функцией либо критерием оптимизации:
Вектор управления, который обеспечивает экстремум I, называется вектором оптимального управления U0 Задача оптимизации решается в два этапа: 1) вырабатывается вектор задающих воздействий
2) отрабатываются эти задающие воздействия, т.е. они преобразуются в управляющие При синтезе оптимальной системы управления возможны два типа задач: 1) известна структура системы и необходимо найти оптимальное значение параметров регулятора; 2) задан ОУ и необходимо найти структуру и параметры регулятора; В случае, если объект является стационарным и отсутствуют внешние возмущения, то при оптимальном управлении можно ограничиться таким алгоритмом управления, который определит неизменную настройку регулятора. При этом должна быть известна информация о внутренних и внешних возмущениях. Для нестационарных объектов система должна работать в условиях неопределенности. В этом случае используют принцип адаптации, который позволяет автоматически изменить алгоритм и параметры настройки регулятора. Пример адаптивной системы
Здесь О - объект управления, УУ - управляющее устройство, состоящее из двух частей: УУ о и УУа, где УУ о - основное управляющее устройство, а УУа - управляющее устройство адаптации. Контур, образованный УУ о и О,является основным контуром системы и представляет собой обычную неадаптивную САУ. Управляющее устройство адаптации УУа управляет основным управляющим устройством УУ о, изменяя его оператор, т. е. схему и значения параметров, в соответствии с изменением внешних условий работы и свойств объекта. Для этого УУа измеряет в самом общем случае внешние воздействия G и F и выходную и входную величины объекта Y и U. По этим данным определяется значение критерия качества управления J (Y, U, G, F). В зависимости от алгоритма работы устройство УУ а определяет отклонение критерия качества J от заданного или от экстремального его значения и воздействует на УУ о так, чтобы ликвидировать это отклонение. Причиной изменения критерия качества J может быть изменение внешних условий работы в виде изменений каких-либо характеристик воздействий G и F или изменение свойств основного контура, т.е. операторов объекта О и основного управляющего устройства УУ о. Таким образом, адаптивная САУ содержит два контура управления – основной контур и второй контур – контур адаптации, создаваемый управляющим устройством адаптации УУа. Для этого второго контура объектом управления является вся основная САУ. Контур адаптации образует второй уровень управления, второй этаж над основной САУ. Возможен и следующий уровень адаптации, когда управляющее устройство адаптации УУ а, в свою очередь, подстраивается, изменяется следующим управляющим устройством, которое при изменении внешних условий или свойств первичной адаптивной САУ изменяет алгоритм адаптации, осуществляемой УУа. Аналогично возможны многоступенчатые САУ, содержащие большее число уровней адаптации. У таких САУ каждый последующий уровень управляет предыдущим, расширяя диапазон условий, при которых система будет правильно выполнять свою задачу, или повышая качество ее выполнения в заданном диапазоне.
Критерии оптимизации В качестве критерия оптимизации могут выбираться различные экономические и технико-экономические параметры. При оптимизации статики и установившихся режимов работы многомерных объектов критерии оптимизации формулируются как некоторая функция, характеризующая качество работы объекта.
В качестве критерия оптимизации (на высших уровнях АСУТП) может применяться ф-ция пользы, которая представляет собой некоторую сумму: 1) X – вектор координат состояний объекта Y – вектор выходных состояний объекта U – вектор управляющих воздействий 2) максимум прибыли
g – цена П – производительность S – затраты
3) минимум потерь
Xi(t) – реализуемая переменная технологического процесса Si – стоимость потерь от нестабильности i-ой переменной Во многих случаях качество работы АСУТП оценивается несколькими критериями, часть из которых противоречива. Тогда либо формируют векторный критерий либо используют один показатель качества, а на остальные накладывают ограничения. Векторный критерий оптимизации: От векторного критерия переходят к обобщенному скалярному:
Сi – коэффициент, отражающий вклад частного критерия в общий скалярный
Наиболее распространенными критериями оптимизации на уровне САР являются: 1) обеспечение максимального быстродействия
2) максимальная точность
При использовании в качестве функционала этого критерия в системе возникают процессы с большим перерегулированием 3) λ – коэффициент, ограничивающий скорость переходного процесса, т.е. величину перерегулирования. 4) для стохастических систем в качестве критерия оптимизации можно использовать среднее значение квадрата ошибки
5) расход энергии на управление
6) если используются механические источники энергии
U(t) – управляющее воздействие
7) если на объект управления действуют возмущения (контролируемые и неконтролируемые), то в качестве критерия принят функционал, характеризующий взаимную корреляцию между выходом и возмущением:
В общей постановке задачи оптимизации минимизируемый функционал детерминированных систем можно записать в следующем виде:
F – подынтегральная функция функционала качества (характеризует динамику).
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.236 (0.007 с.) |

 , которые называются координатами состояния (переменными состояния). Эти переменные можно рассмотреть как некоторый вектор в n-мерном пространстве:
, которые называются координатами состояния (переменными состояния). Эти переменные можно рассмотреть как некоторый вектор в n-мерном пространстве:
 , которые называют выходными координатами:
, которые называют выходными координатами: – определяет качество работы системы.
– определяет качество работы системы. – выражают нежелательные изменения выходных координат.
– выражают нежелательные изменения выходных координат.




 à max
à max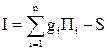 à max
à max à min
à min


 à min
à min à min
à min à min
à min à min
à min à min
à min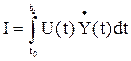 à min
à min – скорость изменения выходного сигнала
– скорость изменения выходного сигнала à min
à min à min
à min – функция, характеризующая качество в конечный момент времени, т.е. после завершения переходного процесса.
– функция, характеризующая качество в конечный момент времени, т.е. после завершения переходного процесса.


