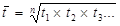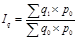Предмет и задачи статистики. История статистики.

Предмет и задачи статистики. История статистики.

Слово «статистика» лат. происхождения и означ. «состояние» (гос-ва). В науку этот термин введен в 18в. Немецким ученым Ахенвалем. Как наука статистика сформировалась в 17в. Однако статистический учет существовал уже в глубокой древности, н-р в 20в. До н.э. в Китае вели учет населения, скота, земли. В 1в. До н.э. в Риме вели учет имущества свободных граждан. В 11в. На Руси в летописях есть сведения о поселениях на водных путях, об имуществе граждан.

Первые переписи населения на Руси проводили во времена Ордынского Ига, но считали не людей, а дома. После 1861 г. учет населения стали проводить по прописанным в домах жителям. Первая научно – организованная перепись была проведена в 1897 г. Предпоследняя перепись – 1998 г. Последняя перепись – 2002 г. У истоков статистической науки стояли 2 школы – Немецкая описательная и Английская школа полит. арифметиков. Представители описательной школы стремились вести описание только в словесной форме, без цифр и вне динамики. Представителем этой школы являлся Ахенваль. Полит. арифметики изучали общие явления с помощью числовых характеристик. Представителями этой школы являлись Грацит – исследовал закономерности массовых явлений, Пети – создатель эк. статистики, Галей – заложил идею закона больших чисел. Он глоссит: «Количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом числе». Школа полит. арифметиков победила. В настоящее время термин «статистика» употребляется в 3х значениях:

· Под «статистикой» понимают отрасль деятельности, к-рая занимается сбором, обработкой, анализом, публикаций данных о различных явлениях общественной жизни.

· Статистикой называют цифровой материал, служащий для характеристики общих явлений.

· Статистикой называют отрасль знания, учебный предмет.

Предметом статистики является количественная сторона массовых общих явлений в неразрывной связи с их качественной стороной. Свой предмет статистика изучает при помощи опр. категорий:

· Статистическая совокупность – совокупность соц.-эк. объектов и явлений общ. Жизни, объединен. Некоторой кач. Основой н-р, совокупность пред-тий, фирм, семей.

· Единица совокупности – первичный элемент статистической совокупности.

· Признак – кач. Особенность единицы совокупности.

· Статистический показатель – понятие отбражает количеств. харак-ки (размеры) признаков общ. явлений.

· Система статистич. Показателей – совокупность статистич. показателей, отражающая взаимосвязи, к-рые существ. между явлениями.

Основными задачами статистики являются:

1. всестороннее исследование глубоких преобразований эк. и соц. процессов на основе научнообоснов. системы показателей.

2. обобщение и прогнозирование тенденций развития разл. отраслей экономики в целом

3. своевременное обеспеч. надежности информации гос., хоз., эк. органов и широкой общ-сти.

 

Особенности статистической методологии. Статистическая совокупность. Закон больших чисел.

Закон больших чисел

Массовый характер общественных законов и своеобразие их действий предопределяет необходимость исследования совокупных данных.

Закон больших чисел порожден особыми свойствами массовых явлений. Последние в силу своей индивидуальности, с одной стороны, отличаются друг от друга, а с другой – имеют нечто общее, обусловленное их принадлежностью к определенному классу, виду. Причем единичные явления в большей степени подвержены воздействию случайных факторов, ежели их совокупность.

Закон больших чисел в наиболее простой форме гласит, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе.

Таким образом, сущность его заключается в том, что в числах, получающихся в результате массового наблюдения, выступают определенные правильности, которые не могут быть обнаружены в небольшом числе фактов.

Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными, отражающими действия постоянных и существенных фактов в данных условиях места и времени. Тенденции и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного случая.

Свой предмет статистика изучает с помощью различных методов:

· Метод массовых наблюдений

· Метод статистических группировок

· Метод динамических рядов

· Метод индексного анализа

· Метод корреляционно-регрессивного анализа связей показателей и т.д.

Полит. арифметики изучали общие явления с помощью числовых характеристик. Представителями этой школы являлись Грацит – исследовал закономерности массовых явлений, Пети – создатель эк. статистики, Галей – заложил идею закона больших чисел.

Статистическая совокупность - множесттво однокачественных, варьирующих явлений. Отдельные элементы,составляющие совокупности - единицы совокупности. Статист.совокупность называется однородной, если самые существенные признаки для каждой её единицы явл. в основном одинаковые и разнородные и,если объединяются разные типы явлений. Частота-повторяемость признаков в совокупности (в ряду распределения).

Признак- характерная черта (свойство) или инная особенность единиц объектов явлений.Признаки делятся на:1) количественные(эти признаки выражены числами.Они играют преобладающую роль в статистике.Это признаки отдельные значения которых отличаются по величине); 2)качественные ((атрибутивные) выражаются в виде понятий, определений, выражаю-х их сущность, качественное состояние); 3) альтеранативные (качественные признаки,которые могут принимать только одно из двух противоположных значений).Признаки отдельных единиц совокупности принимают отдельные значения. Колеблиемость признаков - вариация.

Единицы статистической совокупности и вариация признаков. Статистические показатели.

Явления и процессы в жизни общества характеризуются статистикой с помощью статистических показателей. Статистический показаетль – это количественная оценка свойств изучаемого явления. В статистическом показателе проявляется единство качественной и количественной сторон. Если не определена качественная сторона явления, нельзя определить и его количественную сторону.

Статистика при помощи стат. показателей характеризует: размеры изучаемых явлений; их особенность; закономерности развития; их взаимосвязи.

Статистические показатели подразделяются на учетно – оценочные и аналитические.

Учетно – оценочные показатели отражают объем или уровень изучаемого явления.

Аналитические показатели используются для характеристики особенностей развития явления, распространенности в пространстве, соотношения его частей, взаимосвязи другими явлениями. В качестве аналитических показателей используются: средние величины, показатели структуры, вариации, динамики, степени тесноты и др. Вариация - это многообразие, изменяемость величины признака у отдельных единиц совокупности наблюдения.

Вариация признака - пол - мужской, женский.

Вариация з/п - 10000, 100000, 1000000.

Отдельные значения признака называются вариантами этого признака.

Каждое отдельное явление, подлежащее статистическому изучению, называется

 

Система государственной статистики в Российской Федерации.

Задачи и принципы организации государственного учета. Статистические стандарты Российской Федерации.

Дискретные и интервальные ряды распределения.

Различают 2 вида вариационных рядов:

1. дискретный ряд, когда значение признака в каждой группе задано одним числом. Например, распределение студентов 215 группы по возрасту:

16 лет (варианта) – 17 человек (частота)

17 лет – 6 человек

2. Интервальный ряд, когда признак в каждой группе задан интервалом. Например, распределение студентов 215 группы по росту:

150 – 160 см. – 5 человек и т.д.

Статистические графики. Элементы статистического графика: графический образ, поле графика, пространственные ориентиры, масштабные ориентиры, экспликация графика. Виды графиков по форме графического образу и по образу построения.

Статистический гафик – представляет собой чертеж, на котором при помощи условных геометрических фигур (линий, точек или др. символических знаков) изображаются статистические данные.

Основные элементы статистического графика:

1. Поле графика – место, на котором он выполняется.

2. Графический образ – это символические знаки, с помощью которых изображаются стат. данные (точки, линии, квадраты, груги и т.д.)

3. Пространственные ориентиры определяют размещение графических образов на поле графика. Они задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствие значениям изучаемых показателей.

4. Масштабные ориентиры стат. графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шкал. Масштаб графика – это мера перевода численной величины в графическую. Масштабная шкала – линия, отдельной точки которой читаются как определенного числа. Шкала графика может быть прямолинейной и криволинейной, равномерной и неравномерной.

5. Эксплуатация графика – это пояснение его содержания, включает в себя заголовокграфика, объеснение масштабных шкал, пояснения отдельных элементов графического образа. Заголовок графика в краткой и четкой форме поясняет основное содержание изображаемых данных.

Также на графике дается текст, делающий возможным чтение графика. Цифровые обозначения шкалы дополняются указанием единиц измерения.

Классификация графиков:

По способу построения:

1. диаграмма представляет чертеж на котором стат. информация изображается посредством геометрических фигур или символических знаков. В стат. применяют след. виды диаграмм:

§ линейные

§ столбиковые

§ ленточные (полосовые) графики

§ круговые

§ радиальные

2. Картограмма – это схематическая (контурная) карта, или план местности, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (штриховки, расцветки, точек). Картограмма подразделяется на:

§ Фоновые

§ Точечные

В фоновых картограммах территории с различной величиной изучаемого показателя имеют различную штриховку.

В точечных картограммах в качестве графического знака используются точки одинакого размера, размещенные в пределах определенных территориальных единиц.

3. Картодиаграммы (стат. карты) представляет собой сочетание контурной карты (плана) местности с диаграммой.

По форме применяемых графических образов:

1. В точечных графиках в качестве граф. образов применяется совокупность точек.

2. В линейных графиках граф. образами являются линии.

3. Для плоскостных графиков граф. образами являются геометрические фигуры: прямоугольники, квадраты, окружности.

4. Фигурные графики.

По характеру решаемых задач графики:

Рядов распределения; структуры стат. совокупности; рядов динамики; показателей связи; показателей выполнения заданий.

 

 

Ряды динамики. Виды рядов динамики: моментные и интервальные; абсолютных, относительных и средних величин; с равноотстоящими уровнями и неравноотстоящими уровнями во времени; стационарные и нестационарные.

Ряд динамики- ряд обобщающих показателей за разные периоды времени у одного и того же объекта.

Данные называются уровнями динамики. В зависимости от способа выражения уровней ряды динамики подразделяются на:

- ряды абсолютных величин

- ряды относительных величин

- ряды средних величин

В зависимости от состояния явления на определенные моменты различают:

- интервальные ряды

- моментные ряды

интервальные ряды динамики состоят из уровней, которые характеризуют состояние явления за определенный период и интервал времени, например, за январь, февраль, март и т.д.

моментальные ряды динамики состоят из уровней, которые характеризуют явление только на определенную дату, например, на 1 февраля, 1 марта и т.д.

Ряды динамики могут быть с равноотстоящими (по времени) уровнями и неравноотстоящими (по времени) уровнями.

Средний уровень позволяет описать одним числом всю последовательность данных, поэтому его рассчитывают, когда необходимо сравнить ряды динамики у разных объектов.

В зависимости от вида рядав динамики средний уровень определяют:

1. в интервальных рядах по формуле средней арифметической простой

x – уровни ряда динакими

n - число уровней

 

 

2. в моментных рядах по формуле средней хронологической

x1- начальный уровень ряда

xn- конечный уровень ряда

n- число уровней в ряду.

 

 

37. Показатели изменения уровней рядов динамики: базисные, цепные и средние абсолютные приросты, коэффициенты и темпы роста (прироста).

Анализируют ряды динамики путем сравнения уровней между собой. Если каждый уровень сравнивается с начальным, то получают базисные показатели.

Если каждый уровень сравнивают с предыдущим, то получают цепные показатели.

Существуют следующие виды показателей рядов динамики:

1. абсолютный прирост.

Показывает, на соклько уровень отличается от базы, т.е. от того уровня, с которым сравнивают.

Измеряют в тех же единицах, что и уровень.

x-данный уровень

x_b-базовый уровень(база)

2. тем роста. Показывает, во сколько раз данный уровень отличается от базы. Измеряется в %-тах.

3.
темп прироста. Показывает, на сколько %-тов данный уровеньотличается от базы. Выражается в %-тах.

4. Абсолютное значение 1% прироста.

 

 

Показывает, какое содержание имеется в 1 % прироста. Измеряется в тех же единицах, что и уровень. Расчитывают только для цепных показателей.

Средние темпы роста и прироста.

Важными обобщающими показателями ряда динамики являются:

1. средний темп роста, который определяется по формуле средней геометрической

t1, t2, t3- цепные темпы роста

n- число темпов роста.

Если не заданы цепные темпы роста, то:

x_n- конечный уровень ряда

x1- начальный уровень ряда

n – число уровней в ряду

2. средний темп прироста.

Преобразование рядов динамики.

Если уровни ряда динамики не позволяют сделать выводы о тенденциях развития явления (рост, спад, без изменения) или тенденция не выявляется, то ряды динамики преобразуют.

Основными приемами преобразования рядов динамики являются:

1. укрупнение интервалов.

Заключается в том, что ряд из мелких интервалов заменяют рядом из более крупных интервалов путем суммирования уровней.

2. приведение к одному основанию.

Заключается в том, что начальный уровень принимается за 100%, а все остальные уровни сравниваются с начальным, т.е. получается новый ряд динамики, состоящий из базисных темпов роста.

Этот прием используют, когда необходимо сравнить ряды динамики, состоящие из уровней с разными единицами измерения, либо относящиеся к разным объектам.

 

38. Основные компоненты динамического ряда: основная тенденция (тренд); динамические (конъюнктурные), сезонные и случайные колебания.

Одной из важнейших задач статистики является определением в рядах динамики общей тенденции развития явления.

В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражается уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются).

Однако часто приходится встречаться с такими рядами динамики, в которых уровни ряда претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция развивается неясно.

На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формирует в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременым или носить случайный характер.

Поэтому при анализе динамики речь идет не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития.

Основной тенденцией развития (трендом) называется плавное устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Средние индексы.

Средние арифметические индексы.

Средние арифметические индексы используются, когда известны данные только за базисный период и изменение показателя в текущем периоде, т.е. индивидуальные индексы.

Рассмотрим преобразование агрегатного индекса в средний арифметический на примере индекса физического объема.

Неизвестно q1, поэтому выразим его через индивидуальный индекс

Подставим получившееся выражение в формулу агрегатного индекса

Среднегармонические индексы.

Среднегармонические индексы используются, когда известны данные только за текущий период и изменение показателей по сравнению с базисным периодом,т.е. индивидуальный индекс.

Рассмотрим преобразование агрегатного индекса в средний гармонический на примере индекса цен.

Неизвестно p0, поэтому выразим его черезиндивидуальный индекс цены

Подставим получившееся выражение в формулу общего индекса

Факторный анализ.

Индексный метод не только характеризует динамику сложного явления, но и анализирует влияние на нее отдельных факторов. Многие статичтические показатели, характеризующие различные стороны общественных явлений, находяттся между собой в определенной связи (часто в виде произведения). Все соотношения в таких произведениях могут рассматриваться как факторы, определяющие значение результативного показателя. Поэтому многие экономические показатели тесно связаны между собой и образуют индексные системы.

Система взаимосвязанных индексов дает возможность широко применять индексный метод для изучения взаимосвязей общественны явлений, проведения факторного анализа с целью определения роли отдельных факторов (не зависимых друг от друга). В отечественной статистике принята следующая практика факторного анализа: если результативный показатель можно представить как произведение объемного и качественного факторов, то, определяя влияние объемного фактора на изменение результативного показателя, качестыенный фактор фиксируют на уровне базисного периода; если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода.

Например, индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции (товарообороту в фактических ценах):

 

Т.о., произведение индекса цен на индекс физического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах), т.е. образует индексную систему из этих трех индексов.

Рассмотренная система представляет собой двухфакторные системы (связь результативного признака с двумя факторами). Но общий признак может зависеть от трех, четырех, и более факторов, т.е. связь может быть трехфакторная, четырезфакторная и т.д.

Поэтому общие индексы иогут быть разложены также на три и более факторных индексов, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности.

Применяются два метода разложения общего индекса на частные:

1. метод обособленного (изолированного) изучения факторов;

2. метод последовательно-цепной (взаимосвязанное изучение факторов.

Поскольку явления взаимосвязаны, то основной схемой слудует считать последовательно-цепной анализ факторов, требующий правильного расположения фпакторов при построении модели результативного показателя. На первом месте в модели следует ставить качественный фактор. Увеличение цепи факторов на один фактор каждый раз должно приводить к показателю, имеющему реальный экономический смысл.

При определении влияния первого фактора все остальные факторы сохраняются в числителе и знаменателе на уровне отчесного периода.

При построени второго факторного индекса первый фактор сохраняется на уровне базисног периода, третий и все последующие- на уровне отчетного периода.

При построении третьего факторного индекса первый и второй сохраняются н уровне базисного периода, четвертый и все последующие- на уровне отчетного периода и т.д.

 

 

По виду

–индивидуальный- в выборку отбираются отдельные единицы генеральной совокупности

-групповой- в выборку попадают качественно однородные группы или серии изучаемых единиц

-комбинированный отбор (предполагает сочетание 1 и 2 видов)

2. по методу отбора

-повторный

-бесповторный вид выборки

При повторной выборке общая численность единиц генеральной совокупности в процессе выборки неизменна. Единицу, попавшую в выборку после регистрации снова возвращают в генеральную совокупность- «отбор по схеме возвращенного шара»

При бесповторной выборке единица совокупности, попавшая в выборку в генеральную совокупность возвращается и в дальнейшем в выборке не участвует (отбор по схеме невозвращенного шара)

3. по степени охвата единиц совокупности:

-большие выборки

-малые выборки(малая выборка (n<20))

По методу отбора

-повторный

-бесповторный вид выборки

При повторной выборке общая численность единиц генеральной совокупности в процессе выборки неизменна. Единицу, попавшую в выборку после регистрации снова возвращают в генеральную совокупность- «отбор по схеме возвращенного шара». Повторная выборка в социально-экономической жизни встречается редко. Обычно выборку организуют по схеме бесповторной выборки.

При бесповторной выборке единица совокупности, попавшая в выборку в генеральную совокупность возвращается и в дальнейшем в выборке не участвует (отбор по схеме невозвращенного шара). Т.о., при бесповторной выборки численность единиц генеральной совокупности сокращается в процессе исследования.

3. по степени охвата единиц совокупности:

-большие выборки

-малые выборки(малая выборка (n<20))

Малая выборка в статистике.

Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4-5 единиц.

В торговле к малой выборке прибегают, когда большая выборка или невозможна, или нецелесообразна (например, если проведение исследования связано с порчей или уничтожением обследуемых образцов).

Величина ошибки малой выборки определяется по формулам, отличным от формул выборочного наблюдения со сравнительно большим объемом выборки(n>100). Средняя ошибка малой выборки вычисляется по формуле:

Предельная ошибка малой выборки определяется по формуле:

 

t- коэффициент доверия, зависящий от вероятности (P), с какой предельная ошибка определяется

μ- средняя ошибка выборки.

При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n.

Посредством малой выборки в торговле решается ряд практических задач, прежде всего установление предела, в котором находится генеральная средняя изучаемого признака.

 

 

Предмет и задачи статистики. История статистики.

Слово «статистика» лат. происхождения и означ. «состояние» (гос-ва). В науку этот термин введен в 18в. Немецким ученым Ахенвалем. Как наука статистика сформировалась в 17в. Однако статистический учет существовал уже в глубокой древности, н-р в 20в. До н.э. в Китае вели учет населения, скота, земли. В 1в. До н.э. в Риме вели учет имущества свободных граждан. В 11в. На Руси в летописях есть сведения о поселениях на водных путях, об имуществе граждан.

Первые переписи населения на Руси проводили во времена Ордынского Ига, но считали не людей, а дома. После 1861 г. учет населения стали проводить по прописанным в домах жителям. Первая научно – организованная перепись была проведена в 1897 г. Предпоследняя перепись – 1998 г. Последняя перепись – 2002 г. У истоков статистической науки стояли 2 школы – Немецкая описательная и Английская школа полит. арифметиков. Представители описательной школы стремились вести описание только в словесной форме, без цифр и вне динамики. Представителем этой школы являлся Ахенваль. Полит. арифметики изучали общие явления с помощью числовых характеристик. Представителями этой школы являлись Грацит – исследовал закономерности массовых явлений, Пети – создатель эк. статистики, Галей – заложил идею закона больших чисел. Он глоссит: «Количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом числе». Школа полит. арифметиков победила. В настоящее время термин «статистика» употребляется в 3х значениях:

· Под «статистикой» понимают отрасль деятельности, к-рая занимается сбором, обработкой, анализом, публикаций данных о различных явлениях общественной жизни.

· Статистикой называют цифровой материал, служащий для характеристики общих явлений.

· Статистикой называют отрасль знания, учебный предмет.

Предметом статистики является количественная сторона массовых общих явлений в неразрывной связи с их качественной стороной. Свой предмет статистика изучает при помощи опр. категорий:

· Статистическая совокупность – совокупность соц.-эк. объектов и явлений общ. Жизни, объединен. Некоторой кач. Основой н-р, совокупность пред-тий, фирм, семей.

· Единица совокупности – первичный элемент статистической совокупности.

· Признак – кач. Особенность единицы совокупности.

· Статистический показатель – понятие отбражает количеств. харак-ки (размеры) признаков общ. явлений.

· Система статистич. Показателей – совокупность статистич. показателей, отражающая взаимосвязи, к-рые существ. между явлениями.

Основными задачами статистики являются:

1. всестороннее исследование глубоких преобразований эк. и соц. процессов на основе научнообоснов. системы показателей.

2. обобщение и прогнозирование тенденций развития разл. отраслей экономики в целом

3. своевременное обеспеч. надежности информации гос., хоз., эк. органов и широкой общ-сти.