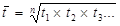Мода. Медиана. Квартили, децили и перцентили. Квартильные и децильные коэффициенты.

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения иструктуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода M_o - значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду- вариант, имеющий наибольшую частоту.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

 

x_Mo – нижняя граница модального интервала

i_Mo – модальный интервал

f _Mo, f _Mo-1, f _Mo+1 – частоты в модальном, предыдущим и следующим за модальным интервалах (соответственно).

Модальный интервал определяется по наибольшей частоте.

Мода широко используется в статистияческой практике при изучении покупательского спроса, регистрации цен и т.п.

Медиана M_e – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части- со сначениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

Номер медианы для нечетного объема вычисляется по формуле:

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные части по численности части) оказывается в каком-то из интервалов признака x. Этот интервал характерен тем, что его кумулятивная частота (накорпленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерномацией по формуле:

 

Где X_Me – нижняя граница медианного интервала,

i_Me – медианный интервал,

Σf/2 – половина от общего числа наблюдений,

S_Me-1 – сумма наблюдений, накопленная до начала медианного интервала,

f_Me – число наблюдений в медианном интервале.

Формула получена, исходя из допущения о равномерности нарастания накопленой частоты внутри интервала и пригодна для любого интервального ряда.

Мода и медиана, как правило, являются дополнительными к средней характеристикам совокупности и используются в математической статистике для анализа формы рядов распределения.

Аналогично медиане вычисляются значения признака, делящие совокупность на четыре (равные по числу единиц) части на пять равных частей- квинтели, на десять частей- децели, на сто частей- перцели.

 

 

Ряды динамики. Виды рядов динамики: моментные и интервальные; абсолютных, относительных и средних величин; с равноотстоящими уровнями и неравноотстоящими уровнями во времени; стационарные и нестационарные.

Ряд динамики- ряд обобщающих показателей за разные периоды времени у одного и того же объекта.

Данные называются уровнями динамики. В зависимости от способа выражения уровней ряды динамики подразделяются на:

- ряды абсолютных величин

- ряды относительных величин

- ряды средних величин

В зависимости от состояния явления на определенные моменты различают:

- интервальные ряды

- моментные ряды

интервальные ряды динамики состоят из уровней, которые характеризуют состояние явления за определенный период и интервал времени, например, за январь, февраль, март и т.д.

моментальные ряды динамики состоят из уровней, которые характеризуют явление только на определенную дату, например, на 1 февраля, 1 марта и т.д.

Ряды динамики могут быть с равноотстоящими (по времени) уровнями и неравноотстоящими (по времени) уровнями.

Средний уровень позволяет описать одним числом всю последовательность данных, поэтому его рассчитывают, когда необходимо сравнить ряды динамики у разных объектов.

В зависимости от вида рядав динамики средний уровень определяют:

1. в интервальных рядах по формуле средней арифметической простой

x – уровни ряда динакими

n - число уровней

 

 

2. в моментных рядах по формуле средней хронологической

x1- начальный уровень ряда

xn- конечный уровень ряда

n- число уровней в ряду.

 

 

37. Показатели изменения уровней рядов динамики: базисные, цепные и средние абсолютные приросты, коэффициенты и темпы роста (прироста).

Анализируют ряды динамики путем сравнения уровней между собой. Если каждый уровень сравнивается с начальным, то получают базисные показатели.

Если каждый уровень сравнивают с предыдущим, то получают цепные показатели.

Существуют следующие виды показателей рядов динамики:

1. абсолютный прирост.

Показывает, на соклько уровень отличается от базы, т.е. от того уровня, с которым сравнивают.

Измеряют в тех же единицах, что и уровень.

x-данный уровень

x_b-базовый уровень(база)

2. тем роста. Показывает, во сколько раз данный уровень отличается от базы. Измеряется в %-тах.

3.

темп прироста. Показывает, на сколько %-тов данный уровеньотличается от базы. Выражается в %-тах.

4. Абсолютное значение 1% прироста.

 

 

Показывает, какое содержание имеется в 1 % прироста. Измеряется в тех же единицах, что и уровень. Расчитывают только для цепных показателей.

Средние темпы роста и прироста.

Важными обобщающими показателями ряда динамики являются:

1. средний темп роста, который определяется по формуле средней геометрической

t1, t2, t3- цепные темпы роста

n- число темпов роста.

Если не заданы цепные темпы роста, то:

x_n- конечный уровень ряда

x1- начальный уровень ряда

n – число уровней в ряду

2. средний темп прироста.

Преобразование рядов динамики.

Если уровни ряда динамики не позволяют сделать выводы о тенденциях развития явления (рост, спад, без изменения) или тенденция не выявляется, то ряды динамики преобразуют.

Основными приемами преобразования рядов динамики являются:

1. укрупнение интервалов.

Заключается в том, что ряд из мелких интервалов заменяют рядом из более крупных интервалов путем суммирования уровней.

2. приведение к одному основанию.

Заключается в том, что начальный уровень принимается за 100%, а все остальные уровни сравниваются с начальным, т.е. получается новый ряд динамики, состоящий из базисных темпов роста.

Этот прием используют, когда необходимо сравнить ряды динамики, состоящие из уровней с разными единицами измерения, либо относящиеся к разным объектам.

 

38. Основные компоненты динамического ряда: основная тенденция (тренд); динамические (конъюнктурные), сезонные и случайные колебания.

Одной из важнейших задач статистики является определением в рядах динамики общей тенденции развития явления.

В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражается уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются).

Однако часто приходится встречаться с такими рядами динамики, в которых уровни ряда претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция развивается неясно.

На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формирует в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременым или носить случайный характер.

Поэтому при анализе динамики речь идет не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития.

Основной тенденцией развития (трендом) называется плавное устойчивое изменение уровня явления во времени, свободное от случайных колебаний.