

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
использования автомобильных транспортных средств
Для планирования, учета и анализа работы подвижного состава грузового автомобильного транспорта установлена система показателей, позволяющая оценить степень использования ПС и результаты его работы.
К показателям, характеризующим степень использования ПС, относятся следующие показатели:
- коэффициент выпуска подвижного состава на линию, aв;
- коэффициент технической готовности подвижного состава, aт;
- коэффициент статического использования грузоподъемности, gс;
- коэффициент динамического использования грузоподъемности, gд;
- коэффициент использования пробега, b;
- средняя длина ездки, L ег;
- среднее расстояние перевозки груза, L гр;
- время простоя ПС под погрузкой-разгрузкой, t пр;
- время в наряде, Т н;
- техническая скорость движения, V т;
- эксплуатационная скорость, V э.
Расчет данных показателей осуществляется по результатам выполненной маршрутизации перевозок и построенных на основании этого эпюр грузопотоков на маршрутах.
Коэффициент статического использования грузоподъемности определяется отношением фактически перевезенного груза Qф к грузу Q, который можно было бы перевезти при условии полного использования грузоподъемности ПС при груженых ездках
gс = Qф / Q. (5.1)
Коэффициент динамического использования грузоподъемности определяется отношением фактически выполненной транспортной работы Wе к возможной работе Wв при условии полного использования грузоподъемности ПС на протяжении всего маршрута с грузом
gд = W е / W в; (5.2)
W e = S Qi Lij; (5.3)
W в = qi L ег. (5.4)
Коэффициент использования пробега подвижного состава определяется отношением производительного пробега к общему за определенный период времени
b = L ег / L м. (5.5)
Среднее расстояние перевозки груза – это средняя дальность транспортирования одной тонны груза, определяется отношением выполненной транспортной работы W е к объему перевезенного груза Q ф
L гр = W е / Q ф. (5.6)
Маршруты работы автомобилей приведены в таблице 5.1.
Таблица 5.1 – Определение количества завозимого в каждый пункт груза
| № п/п
| Автомобиль
| Маршрут следования
| Длина маршрута, км
| Масса доставляемого груза с учетом коэффициента использования грузоподъемности, т
| |
| МАЗ 437040-020
| Б – М1 – М2 – М3 - М4 – М5- М6 - Б
| 38,100
| 4,686
| |
| ЗИЛ- 5301ВА
| Б – М1 – М2 – М3 - М4 – М5- М6 - Б
| 38,100
| 1,8
| |
| МАЗ 437040-020
| Б - М6 – М5 – М4 - М3 – М2- М1 - Б
| 38,100
| 4,686
| |
| ЗИЛ- 5301ВА
| Б - М6 – М5 – М4 - М3 – М2- М1 - Б
| 38,100
| 1,8
|
Для первого маршрута:
- коэффициент статического использования грузоподъемности равен
gс = 4.686/ 4.7 = 0,997;
- коэффициент динамического использования грузоподъемности равен
W e =  ; ;
W в = 4.7 · 27.8 = 130.66 т·км;
gд = 79.378 / 130.66 = 0,6;
- коэффициент использования пробега равен
b = 27.800 / 38.100 = 0,73;
- среднее расстояние перевозки груза равно
L гр = 79.378 / 4.686 = 16,94 км.
Весь последующий расчет технико-эксплуатационных показателей маршрутов выполняется аналогичным образом и представлен в таблице 5.2.
Таблица 5.2 – Показатели использования автомобилей на маршрутах
| Маршрут
| L м, км
| Q, т
| W e, т-км
| gс
| gд
| b
| L гр
| |
| 38,100
| 4,686
| 79,378
| 0,997
| 0,6
| 0,73
| 16,94
| |
| 38,100
| 1,8
| 
| 0,78
| 0,418
| 0,73
| 14,84
| |
| 38,100
| 4,686
| 
| 0,997
| 0,611
| 0,908
| 21,15
| |
| 38,100
| 1,8
| 
| 0,78
| 0,668
| 0,908
| 23,1
|
Согласно полученным результатам суммарная транспортная работа по существующему маршруту равна 106,095 т∙км в сутки, а суточный объем перевозок составляет 6,486 т. Длина маршрута составляет 38,100 км. Коэффициент статического использования грузоподъемности изменяется от 0,997 до 0,78. Среднее расстояние перевозки груза – 16,94 и 14,84 км.
Суммарная транспортная работа по предложенному(обратному) маршруту равна 140,701 т∙км в сутки, а суточный объем перевозок составляет 6,486 т. Длина маршрута составляет 38,100 км. Коэффициент статического использования грузоподъемности изменяется от 0,997 до 0,78. Среднее расстояние перевозки груза – 21,15 и 23,1 км.
Таким образом данные показатели являются весьма приемлемыми в сложившихся условиях перевозок продукции.
Сравнительный анализ существующего и
предлагаемого вариантов
Сравним полученные технико-эксплуатационные показатели для существующего и предлагаемого вариантов.
Для существующего варианта:
а) выполненная транспортная работа W e = 106,095 т-км;
б) общий пробег L м = 38,100 км.
Для предлагаемого варианта:
а) выполненная транспортная работа W e = 140,701 т-км;
б) общий пробег L м = 38,100 км.
В результате сравнения видно, что существующий вариант более эффективен и применим к данной транспортной сети.
ЗАКЛЮЧЕНИЕ
В ходе данной курсовой работы были определены кратчайшие расстояния между пунктами транспортной сети с использованием компьютерной программы NAKRA. Были оптимизированы грузовые потоки при развозе 3-х видов грузов по 6 магазинам города Гомеля, а также были составлены маршруты перевозки этих грузов. Был выбран подвижной состав для осуществления данных перевозок.
Кроме того, были рассчитаны основные технико-эксплуатационные показатели работы подвижного состава и был произведен сравнительный анализ существующего и предлагаемого вариантов маршрутов перевозок грузов. В результате чего был выбран предлагаемый маршрут с движением в прямом напрвлении Б – М1 – М2 – М3 – М4 – М5 – М6– Б, транспортная работа которого составляет 106,095 т-км, а общий пробег автомобилейработающих на данном маршруте 38,1 км, так как он является наиболее выгодным и целесообразным для данного района города Гомеля.
Литература
1 Автомобильные перевозки пассажиров и грузов. Практикум: учебное пособие / С.А. Аземша, С.В. Скирковский, С.В. Сушко; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. - Гомель: БелГУТ, 2012. - 205 с.
2 Требования по оформлению отчетных документов самостоятельной работы студентов: учебно-методическое пособие / М.А. Бойкачев [и др.]; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. - Гомель: БелГУТ, 2008. - 62 с.
3 http://www.uchimatchast.ru/aplication/litl0.php - ипользовали для решения задачи коммивояжера методом Литтла.
ПРИЛОЖЕНИЕ А
M (М1,Б) = М1 - Б; L = 3500 м
M (М2,Б) = М2 - 7 - М1 - Б; L = 8500 м
M (М3,Б) = М3 - 11 - М1 - 7 - М2 - 8 - 9 - 10 - Б; L = 12400 м
M (М4,Б) = М4 - 33 - М1 - 29 - 30 - 31 - 32 - Б; L = 7800 м
M (М5,Б) = М5 - 16 - М1 - 18 - 17 - М6 - Б; L = 14200 м
M (М6,Б) = М6 - 18 - М1 - Б; L = 10300 м
из/в Б М1 М2 М3 М4 М5 М6
Б ---- 3500 8500 12400 7800 14200 10300
М1 3500 ---- 5000 8900 4300 10700 6800
М2 8500 5000 ---- 3900 8800 15300 11800
М3 12400 8900 3900 ---- 5000 11500 14900
М4 7800 4300 8800 5000 ---- 6500 9900
М5 14200 10700 15300 11500 6500 ---- 3900
М6 10300 6800 11800 14900 9900 3900 ----
| Начальный пункт
| Конечный пункт
| | Б
| М1
| М2
| М3
| М4
| М5
| М6
| | Б
| -
|
|
|
|
|
|
| | М1
|
| -
|
|
|
|
|
| | М2
|
|
| -
|
|
|
|
| | М3
|
|
|
| -
|
|
|
| | М4
|
|
|
|
| -
|
|
| | М5
|
|
|
|
|
| -
|
| | М6
|
|
|
|
|
|
| -
|
ПРИЛОЖЕНИЕ Б
В настоящее время в условиях значительного роста объема перевозок грузов в городах для обеспечения более рационального использования подвижного состава и сокращения транспортных затрат большое значение имеет определение кратчайших расстояний между пунктами транспортной сети.
Транспортная сеть представляет собой систему дорог, которые пригодны по качеству дорожного покрытия, ширине проезжей части и открыты для движения подвижного состава.
Транспортная сеть состоит из отдельных элементов, которые являются вершинами и звеньями сети. Каждой вершине присваивается свой порядковый номер или другое условное обозначение.
Получим матрицу стоимости для нашего графа, элементами которой являются веса соответствующих дуг. Все элементы по диагонали матрицы приравнивняем к бесконечности

Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
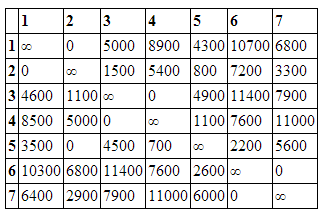
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
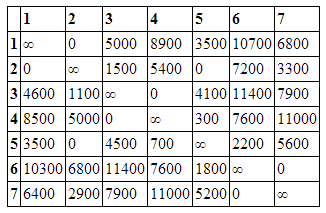
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,5=300, Г3,4=1800, Г4,3=1800, Г5,2=700, Г6,7=5100, Г7,6=5100,
В результате сравнения мы получили 2 одинаковых максимальных Г=5100. Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант Г6,7=5100
Удалим из матрицы стоимости строку 6 и столбец 7, и присвоим элементу (7,6) значение бесконечности. Внесем в текущий ориентированный граф дугу (6,7)

В строке 7 и столбце 6 отсутствует элемент равный ∞. Присвоим элементу (7,6) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=27700
Нижняя граница равна сумме всех вычтенных элементов в строках и столбцах. Итоговое значение нижней границы должно совпасть с длиной результирующего контура.
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
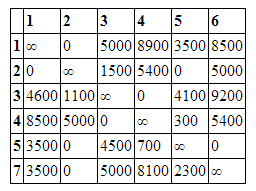
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,5=300, Г3,4=1800, Г4,3=1800, Г5,2=0, Г5,6=5000, Г7,2=2300,
Максимальное значение имеет Г5,6=5000
Удалим из матрицы стоимости строку 5 и столбец 6. Внесем в текущий ориентированный граф дугу (5,6)
В строке 7 и столбце 5 отсутствует элемент равный ∞. Присвоим элементу (7,5) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=32800
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,5=300, Г3,4=6500, Г4,3=1800, Г7,2=3500,
Максимальное значение имеет Г3,4=6500
Удалим из матрицы стоимости строку 3 и столбец 4. Внесем в текущий ориентированный граф дугу (3,4)
В строке 4 и столбце 3 отсутствует элемент равный ∞. Присвоим элементу (4,3) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=32800
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,3=3500, Г2,5=0, Г4,5=4700, Г7,2=3500,
Максимальное значение имеет Г4,5=4700
Удалим из матрицы стоимости строку 4 и столбец 5. Внесем в текущий ориентированный граф дугу (4,5)
В строке 7 и столбце 3 отсутствует элемент равный ∞. Присвоим элементу (7,3) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=34600
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,3=3500, Г7,2=3500,
В результате сравнения мы получили 4 одинаковых максимальных Г=3500. Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант Г1,2=3500
Удалим из матрицы стоимости строку 1 и столбец 2, и присвоим элементу (2,1) значение бесконечности. Внесем в текущий ориентированный граф дугу (1,2)
В строке 2 и столбце 1 отсутствует элемент равный ∞. Присвоим элементу (2,1) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=34600
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (1, 2), (2, 3), (7, 1)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г7,2. Удалим из матрицы стоимости строку 2 и столбец 7. Внесем в текущий ориентированный граф дугу (7,2)
В строке 2 и столбце 3 отсутствует элемент равный ∞. Присвоим элементу (2,3) значение бесконечности чтобы избежать преждевременногог замыкания контура.
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (7, 2), (1, 3), (2, 1)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г2,3. Удалим из матрицы стоимости строку 3 и столбец 2. Внесем в текущий ориентированный граф дугу (2,3)
В строке 7 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (7,2) значение бесконечности чтобы избежать преждевременногог замыкания контура.
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (2, 3), (1, 2), (7, 1)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г2,1. Удалим из матрицы стоимости строку 1 и столбец 2. Внесем в текущий ориентированный граф дугу (2,1)
В строке 1 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (1,2) значение бесконечности чтобы избежать преждевременногог замыкания контура.
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (2, 1), (1, 3), (7, 2)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г7,6. Удалим из матрицы стоимости строку 6 и столбец 7. Внесем в текущий ориентированный граф дугу (7,6)
В строке 6 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (6,7) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,5=0, Г2,7=2300, Г3,4=1800, Г4,3=1800, Г5,2=700, Г6,5=5000,
Максимальное значение имеет Г6,5=5000
Удалим из матрицы стоимости строку 6 и столбец 5. Внесем в текущий ориентированный граф дугу (6,5)
В строке 5 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (5,7) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=32800
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,7=3500, Г3,4=1800, Г4,3=6500, Г5,2=700,
Максимальное значение имеет Г4,3=6500
Удалим из матрицы стоимости строку 4 и столбец 3. Внесем в текущий ориентированный граф дугу (4,3)
В строке 3 и столбце 4 отсутствует элемент равный ∞. Присвоим элементу (3,4) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=32800
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,7=3500, Г3,2=3500, Г5,2=0, Г5,4=4700,
Максимальное значение имеет Г5,4=4700
Удалим из матрицы стоимости строку 5 и столбец 4. Внесем в текущий ориентированный граф дугу (5,4)
В строке 3 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (3,7) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=34600
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г1,2=3500, Г2,1=3500, Г2,7=3500, Г3,2=3500,
В результате сравнения мы получили 4 одинаковых максимальных Г=3500. Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант Г1,2=3500
Удалим из матрицы стоимости строку 1 и столбец 2, и присвоим элементу (2,1) значение бесконечности. Внесем в текущий ориентированный граф дугу (1,2)
В строке 2 и столбце 1 отсутствует элемент равный ∞. Присвоим элементу (2,1) значение бесконечности чтобы избежать преждевременногог замыкания контура.
Текущая Нижняя граница=34600
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (1, 2), (2, 7), (3, 1)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г3,2. Удалим из матрицы стоимости строку 2 и столбец 3. Внесем в текущий ориентированный граф дугу (3,2)
В строке 2 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (2,7) значение бесконечности чтобы избежать преждевременногог замыкания контура.
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (3, 2), (1, 7), (2, 1)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г2,7. Удалим из матрицы стоимости строку 7 и столбец 2. Внесем в текущий ориентированный граф дугу (2,7)
В строке 3 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (3,2) значение бесконечности чтобы избежать преждевременногог замыкания контура.
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (2, 7), (1, 2), (3, 1)
-------------------------------------------------------------------------
Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г2,1. Удалим из матрицы стоимости строку 1 и столбец 2. Внесем в текущий ориентированный граф дугу (2,1)
В строке 1 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (1,2) значение бесконечности чтобы избежать преждевременногог замыкания контура.
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы.
НГр=38100
Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (2, 1), (1, 7), (3, 2)
-------------------------------------------------------------------------
Мы рассмотрели все возможные ветви алгоритма, теперь необходимо выбрать из полученых в результате рассмотрения каждой ветви значений нижней границы - минимальное. Это и будет оптимальной длиной пути коммивояжера
Минимальное значение имеет НГр=38100
Соответствующий оптимальный контур включет дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (1, 2), (2, 3), (7, 1)
|



 ;
;











