Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Маршрутизация перевозок мелкопартийных грузовСодержание книги
Поиск на нашем сайте
Выберем маршруты движения автомобилей. Для этого необходимо определить оптимальную последовательность объезда всех грузопоглащающих узлов транспортной сети, т.е. решить задачу коммивояжера. Исходными данными для этого выступает матрица кратчайших расстояний (таблица 2.1). Приведем матрицу расстояний по строкам (таблица 3.1) Таблица 3.1 – Приведение матрицы по строкам
Приведем матрицу расстояний по столбцам (таблица 3.2) Таблица 3.2 – Приведение матрицы по столбцам
Полностью приведенная матрица приведена в таблице 3.3. Таблица 3.3 – Полностью приведенная матрица
Определим нижнюю границу множества Гамильтоновых контуров:
Каждый нуль в приведенной матрице (см. таблицу 1.6) условно заменяем на Таблица 3.4 – Определение сумм констант приведения
Из таблицы 3.4 видно, что наибольшее значение суммы констант приведения получается на пересечении 6й строки и 7-го столбца и 7й строки и 6го столбца и составляет 5100. Рассмотрим первый вариант. Априорно исключаем из гамильтонова контура дугу (6,7), заменяя элементы а 7,6 = 0 в матрице расстояний на Приводим полученную матрицу расстояний и определяем нижнюю границу Таблица 3.5 – Исключение 6 строки и 7 столбца
Таблица 3.6 – Приведение матрицы по строкам
Таблица 3.7 – Приведение матрицы по столбцам
Тогда Каждый нуль в полученной матрице условно заменяем на Таблица 3.8 – Полностью приведенная матрица
Таблица 3.9 – Определение сумм констант приведения
Из таблицы 3.9 видно, что наибольшее значение суммы констант приведения получается на пересечении 5 строки и 6 столбца и составляет 5000. Априорно исключаем из гамильтонова контура дугу (5,6) и проводим расчеты аналогичные предыдущим. Таблица 3.10 – Исключение 5й строки и 6го столбца
Таблица 3.11 – Приведение матрицы по строкам
Таблица 3.12 – Приведение матрицы по столбцам
Тогда Каждый нуль в полученной матрице условно заменяем на Таблица 3.13 – Полностью приведенная матрица
Таблица 3.14 – Определение сумм констант приведения
Из таблицы 3.14 видно, что наибольшее значение суммы констант приведения получается на пересечении 3 строки и 4 столбца и составляет 6500. Априорно исключаем из гамильтонова контура дугу (3,4), заменяя элемент а 4,3 = 3100 в матрице расстояний на Таблица 3.15 – Исключение 3 строки и 4 столбца
Таблица 3.16 – Приведение матрицы по строкам
Таблица 3.17 – Приведение матрицы по столбцам
Тогда Каждый нуль в полученной матрице условно заменяем на Таблица 3.18 – Полностью приведенная матрица
Таблица 3.19 – Определение сумм констант приведения
Из таблицы 3.19 видно, что наибольшее значение суммы констант приведения получается на пересечении 3 строки и 3 столбца и составляет 4700. Априорно исключаем из гамильтонова контура дугу (3,4), заменяя элемент а 4,3 = 3500 в матрице расстояний на Таблица 3.20 – Исключение 4 строки и 3 столбца
Таблица 3.21 – Приведение матрицы по строкам
Таблица 3.22 – Приведение матрицы по столбцам
Тогда Таблица 3.23 – Полностью приведенная матрица
Каждый нуль в полученной матрице условно заменяем на Таблица 3.24 – Определение сумм констант приведения
Из таблицы 3.24 видно, что мы получили 4 одинаковых максимальных суммы констант приведения (3500). Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант (1,2). Априорно исключаем из гамильтонова контура дугу (1,2), заменяя элемент а 2,1 = 0 в матрице расстояний на Таблица 3.25 – Исключение первой строки и второго столбца
Текущая Нижняя граница=34600 После того, как рассмотрели все возможные ветви алгоритма, выберем из полученных в результате рассмотрения каждой ветви значений нижней границы - минимальное. Это и будет оптимальной длиной пути коммивояжера. Минимальное значение имеет НГр=38100. Соответствующий оптимальный контур включает дуги: (М5,М6), (М4,М5), (М2, М3), (М3, М4), (Б, М1), (М1, М2), (М6, Б).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.006 с.) |
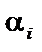
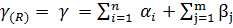= 27700
и находим сумму констант приведения 
. Значения 
записываем в соответствующие клетки рядом с нулями (таблица 3.4).
}.
подмножества гамильтоновых контуров { 
а 
Матрица, полученная после приведения по строкам и столбцам приведена в таблице 3.8.
а 
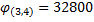Матрица, полученная после приведения по строкам и столбцам приведена в таблице 3.13.
а 
Матрица, полученная после приведения по строкам и столбцам приведена в таблице 3.18.
а 
Матрица, полученная после приведения по строкам и столбцам приведена в таблице 3.23.
