
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні залежності при згинанніСодержание книги
Поиск на нашем сайте
Виділимо малий елемент dx- це О1О2
∑Y=0 Q+q∙dx-(Q+dQ)=0 è
∑Mo2=0 M+Q∙dx+(q∙dx∙dx)/2-(M+dM)=0
M +Q∙dx+q∙ (dx)2/2- M -dM=0
q∙ (dx)2/2=0 в силу его малости
Побудова епюр при згині балок
∑МА=0 qa∙2a-q∙2a∙a-2qa2-RB∙2a=0 RB=-qa ∑МB=0 qa∙4a-q∙2a∙3a+RA∙2a-2qa2=0 RA=2qa ∑Yi=0 P-2qa+RA-RB=0 qa -2qa+2qa-qa=0
I 0 ≤ x ≤ 2a Q(x)= qa-qx M(x)= Px-qx2/2=qa∙x-qx2/2 Q(0)=qa; Q(2a)=-qa M(0)=0 M(2a)=2qa2-2qa2=0 Q(x)=qa-qx=0 x=a M(a)= qa2-qa2/2=qa2/2
II 2a ≤ x ≤ 4a Q(x)=qa-2qa+2qa=qa M(4a)=4qa2-6qa2+4qa2=2qa2 M(x)=qa∙x-2qa∙ (x-a)+2qa∙ (x-2a) M(2a)=2qa2-2qa2=0
Лекція № Визначення нормальних напружень при згинанні При прямому поперечному згинанні у поперечному перерізі балки виникають два внутрішніх зусилля Q та М; залежності між цим зусиллям та напруженнями у поперечному перерізі балки такі:
Отже, в поперечних перерізах балки при згинанні виникають як дотичні напруження так і нормальні напруження. Дотичні напруження при згинанні балок у переважній більшості випадків не враховуються. Особливі випадки коли величиною дотичних напружень знехтувати не можливо, тут не розглядаються. Статична сторона задачі Для виводу формул, що визначають нормальні напруження, які виникають в поперечному перерізі балки, розглянемо балку, що знаходиться в умовах чистого згину (рис. 6.13), тобто Q = 0 і дотичні напруження відсутні. Двома нескінченно близькими поперечними перерізами виділимо з цієї балки елемент довжиною dx (рис. 6.13,а).
Переріз балки прямокутник. В площині перерізу проведемо координатні осі (рис.6.13,б). Приймаємо, що вісь збігається з силовою лінією (лінію перетину силової площини з площиною перерізу); вісь z проведемо перпендикулярно осі у; вісь х направлена перпендикулярно до площини перерізу. У перерізі виділимо елемент з площею dF (точка А), його координати – у, z. При чистому згинанні (Q =0, t = 0) на елемент діє зусилля dN = sdF. Тоді з шести інтегральних рівнянь можна використати три:
Але цих трьох рівнянь статики не достатньо для визначення s, тому що невідомий закон розподілу σ по перерізу та розташування осі Z. Геометрична сторона задачі Розглянемо картину деформацій цієї балки. Якщо на еластичну балку нанести сітку з ліній паралельних і перпендикулярних вісій, то при чистому згинанні прямокутна сітка деформується так що:
1) поздовжні лінії викривлюються по дузі кола; 2) поперечні лінії лишаються прямими і нахиляються одна до одної; 3) поперечні лінії з поздовжніми перетинаються під прямим кутом (рис. 6.13,в).
На основі такої картини можна вважати, що при чистому згині поперечні перерізи лишаються плоскими і повертаються, лишаючись перпендикулярними до осі балки, тобто при чистому згинанні справедлива гіпотеза плоских перерізів. Можна вважати, що відстань а між поперечними перерізами змінюється а 1 < a, a 2 > a, а саме верхні волокна скорочуються, а нижні – витягуються. Очевидно, що серед них є такі волокна які не змінюють своєї довжини. Сукупність таких волокон називаеть нейтральним шаром (рис. 6.13). Лінія перетину нейтрального шару із площиною поперечного перерізу балки називається нейтральною лінією Будемо вважати вісь z нейтральною віссю. Беручи до уваги картину деформацій, зобразимо деформований стан елемента dx (рис. 6.14).
Розглянемо тепер цей елемент після деформування:
Н.С.
Фізична сторона задачі. На елементпрній площадці дотичних напружень немає. Волокна матеріалу не тиснуть одне на одне. Таким чином волокно a b перебуває в лінійному напруженому стані:
/ \
напружень тиснуть одне нема на одне
Синтез:
Формула Нав’є показує, що при згині нормальні напруження розподіляються за лінійним законом.
Тобто вісь z – нейтральна лінія перелізу проходить через центр вала, а вісі у та z – головні центральні вісі перелізу. Формула Нав’є показує, що незалежно від формі та розмірів перерізу балки, напруження в точках нейтральної лінії завжди дорівнюють 0. Величина
Максимальні напруження  мають місце в найбільш віддалених від нейтральної лінії волокнах. У випадку симетричного перерізу: мають місце в найбільш віддалених від нейтральної лінії волокнах. У випадку симетричного перерізу:
осьові моменти опору Якщо переріз балки не має горизонтальної осі симетрії, то нейтральна лінія зміщена відносно середини висоти перерізу, але знову
Для простіших перерізів:
Wz = 2 Iz/h = bh3 2 /12h = bh2/ 6(6-5) Wy = Iy 2 /b = hb2/ 6
Wy = Wz = 2 Iocн/d = pd4/ 64 d = Кільце: Wz = Wy = pD3 (1-a) = 0,1 D3 ( 1 -a), (6-7) де a = d/D – відношення внутрішнього до зовнішнього діаметра кільця. Для прямокутного перерізу
Для кругового
Для кільцевого
Для прокатних профілів значення Wz та Wy вказані у таблицях
Якщо переріз складний то визначаємо Затрати матеріалу пропорційна площі поперечного перерізу F. Отже чим більше відношення W/F, тим більший згинальний момент витримує переріз заданою площею.
умова міцності для нормальних напружень: Тепер можна записати умову міцності для нормальних напружень при згинанні: smax = Mmax/Wz ≤ [s] (6-8) Умова міцності при згинанні дозволяє виконувати три типи розрахунків: перевірочний, проектувальний та визначення допустимого навантаження. Значення [s] береться те ж, що і при розтяганні – стисканні; Мma x – у небезпечному перерізі за епюрою згинального моменту. Якщо розглядаються балки з пластичного матеріалу, не має різниці для яких волокон записати умову міцності – стиснутих або розтягнених, для пластичних матеріалів [s+] = [s -].
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.60 (0.011 с.) |





 .
.
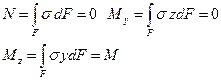

 Виділимо елемент балки двома суміжними поперечними перерізами m – m та n – n, які розташовані один від одного на відстані dx.
Виділимо елемент балки двома суміжними поперечними перерізами m – m та n – n, які розташовані один від одного на відстані dx.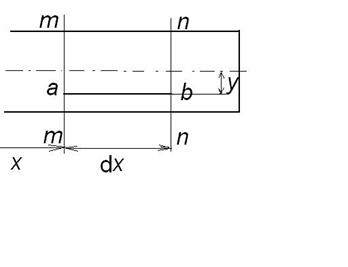


 - радіус кривизни.
- радіус кривизни.
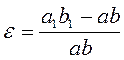
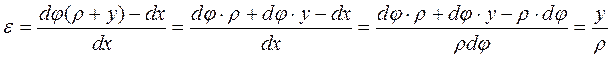




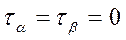 ;
; 


 - закон Гука при згині;
- закон Гука при згині;  (добуток) – називається жорсткістю перерізу при згині
(добуток) – називається жорсткістю перерізу при згині 

 - формула Нав’є.
- формула Нав’є. - Показує, що центр ваги лежить на осі Z.
- Показує, що центр ваги лежить на осі Z. - Показує, що вісі Z та y головні центральні. Тобто вісь Z нейтральна лінія перерізу проходить через центр ваги, а осі y та z – головні центральні осі перерізу.
- Показує, що вісі Z та y головні центральні. Тобто вісь Z нейтральна лінія перерізу проходить через центр ваги, а осі y та z – головні центральні осі перерізу. змінюється лінійно по товщині балки.
змінюється лінійно по товщині балки.

 - осьовий момент опору
- осьовий момент опору 
 де
де 

 Прямокутник:
Прямокутник: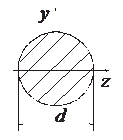 Коло:
Коло: (6-6)
(6-6)




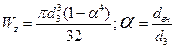
 . Далі знаходимо
. Далі знаходимо  потім
потім  .
.


