
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особливості епюр поперечних сил Q та згинальних моментів MСодержание книги
Поиск на нашем сайте
Лекція№ Згин Плоский згин Прямолінійні стержні, що працюють на згин називаються балками.Якщо всі зовнішні навантаження діють в одній площині, що називаються силовою, причому ця площина збігаеться з однією із головних площин балки, то має місце плоский поперечний згин.
      

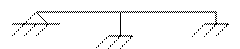
Мкр=0: N=0; Q≠0; M≠0; Види опор та їх реакції 1)Затиснення або жорстке стиснення виникає 3 складові:Ma;Ra;Na.
2)Шарнірно-нерухома опора

3)Шарнірно-рухома опора Виникає тільки вертикальна реакція Ra.
Балки бувають: 1) Однопрольотні 2) Багатопрольотні 3) Консолі Визначення реакцій балки

Перевірка
Тобто Ra та Rb знайшли вірно.
При плоскому згинанні балках при навантаженні, перпендикулярному до осі балки поздовжна сила буде дорівнювати нулю. Тому в будь якому перерізі балки виникають тільки два внутрішніх зусилля: поперечна сила Q та згинальний момент М. Якщо навантаження зосереджене в головній площині стержня x y, то Q z =0; M x =0; M y =0; N=0 так як сили перпендикулярні осі балки. Залишаються:
Залишаються:
Установимо такі правила знаків для Q і М в балках: 1. Поперечна сила Q у перерізі додатна, якщо її вектори намагаються обертати частини розсіченої балки за годинниковою стрілкою.
Q > 0 Q < 0
2. Згинальний момент М у перерізі додатний, якщо він спричиняє стиснення у верхніх волокнах балки і спрямований таким чином:
M > 0 M < 0
Особливості епюр поперечних сил Q та згинальних моментів M
1. На ділянках, де немає розподільного навантаження епюри Q окреслюються прямими, паралельними базі, а епюри М в загальному випадку нахиленими прямими.
2. На ділянках, де до балок прикладене рівномірно розподілене навантаження q, епюра Q обмежується нахиленою прямою, а епюра М – квадратичною параболою. Випуклість параболі звернена в бік протилежний напряму дії навантаження q.
Правило дощику або парасольки:
3. В перерізах де Q = 0, дотична до епюри М паралельна базі епюри.
4. На ділянках де Q > 0, момент зростає, де Q < 0, момент М зменшується.
5. Якщо в шарнірі, або на кінці консолі не прикладений зосереджений момент, то на епюрах моментів М=0.
6. У перерізах, де до балки прикладені зосереджені сили: а) на епюрі Q будуть стрибки на величину і в напрямку дії прикладених сил.
б) на епюрі М будуть переломи, причому вістря перелому спрямоване проти дії сили; 7. У перерізах, де до балки прикладені зосереджені моменти, на епюрі М будуть стрибки на значення цих моментів (на епюрі Q змін не буде); 8. Якщо на кінці консолі або в шарнірі прикладен зосереджений момент, то в цьому перерізі згинальний момент дорівнює зовнішньому моменту.
Епюри Q та M при зміні 1)
Q(x) =-P M(x) =-P*x
2)
Q(X) =- M(X) = 3)
Ra=Rb=
Q(X)=Ra- M(X)=
M(
4)
Q(X)=Ra
M(X)=
M(a)=
5)
Диференціальні залежності при згинанні
Виділимо малий елемент dx- це О1О2
∑Y=0 Q+q∙dx-(Q+dQ)=0 è
∑Mo2=0 M+Q∙dx+(q∙dx∙dx)/2-(M+dM)=0
M +Q∙dx+q∙ (dx)2/2- M -dM=0
q∙ (dx)2/2=0 в силу его малости
Побудова епюр при згині балок
∑МА=0 qa∙2a-q∙2a∙a-2qa2-RB∙2a=0 RB=-qa ∑МB=0 qa∙4a-q∙2a∙3a+RA∙2a-2qa2=0 RA=2qa ∑Yi=0 P-2qa+RA-RB=0 qa -2qa+2qa-qa=0
I 0 ≤ x ≤ 2a Q(x)= qa-qx M(x)= Px-qx2/2=qa∙x-qx2/2 Q(0)=qa; Q(2a)=-qa M(0)=0 M(2a)=2qa2-2qa2=0 Q(x)=qa-qx=0 x=a M(a)= qa2-qa2/2=qa2/2
II 2a ≤ x ≤ 4a Q(x)=qa-2qa+2qa=qa M(4a)=4qa2-6qa2+4qa2=2qa2 M(x)=qa∙x-2qa∙ (x-a)+2qa∙ (x-2a) M(2a)=2qa2-2qa2=0
Лекція № Фізична сторона задачі. На елементпрній площадці дотичних напружень немає. Волокна матеріалу не тиснуть одне на одне. Таким чином волокно a b перебуває в лінійному напруженому стані:
/ \
напружень тиснуть одне нема на одне
Синтез:
Формула Нав’є показує, що при згині нормальні напруження розподіляються за лінійним законом.
Тобто вісь z – нейтральна лінія перелізу проходить через центр вала, а вісі у та z – головні центральні вісі перелізу. Формула Нав’є показує, що незалежно від формі та розмірів перерізу балки, напруження в точках нейтральної лінії завжди дорівнюють 0. Величина
Максимальні напруження  мають місце в найбільш віддалених від нейтральної лінії волокнах. У випадку симетричного перерізу: мають місце в найбільш віддалених від нейтральної лінії волокнах. У випадку симетричного перерізу:
осьові моменти опору Якщо переріз балки не має горизонтальної осі симетрії, то нейтральна лінія зміщена відносно середини висоти перерізу, але знову
Для простіших перерізів:
Wz = 2 Iz/h = bh3 2 /12h = bh2/ 6(6-5) Wy = Iy 2 /b = hb2/ 6
Wy = Wz = 2 Iocн/d = pd4/ 64 d = Кільце: Wz = Wy = pD3 (1-a) = 0,1 D3 ( 1 -a), (6-7) де a = d/D – відношення внутрішнього до зовнішнього діаметра кільця. Для прямокутного перерізу
Для кругового
Для кільцевого
Для прокатних профілів значення Wz та Wy вказані у таблицях
Якщо переріз складний то визначаємо Затрати матеріалу пропорційна площі поперечного перерізу F. Отже чим більше відношення W/F, тим більший згинальний момент витримує переріз заданою площею.
умова міцності для нормальних напружень: Тепер можна записати умову міцності для нормальних напружень при згинанні: smax = Mmax/Wz ≤ [s] (6-8) Умова міцності при згинанні дозволяє виконувати три типи розрахунків: перевірочний, проектувальний та визначення допустимого навантаження. Значення [s] береться те ж, що і при розтяганні – стисканні; Мma x – у небезпечному перерізі за епюрою згинального моменту. Якщо розглядаються балки з пластичного матеріалу, не має різниці для яких волокон записати умову міцності – стиснутих або розтягнених, для пластичних матеріалів [s+] = [s -].
Інтеграл Мора
1) Нехай діє узагальнене навантаження, сила Р1 в точці 1. Переміщення відповідних точок системи будуть Δ11, Δ21 … Δі1.
2) Нехай діє узагальнена сила Р2 в точці 2, переміщення відповідних точок будуть Δ12, Δ22 … Δі2.
Δij – i – номер точки,яка переміщується; j – номер точки прикладання зовнішньої сили, тобто цей індекс вказує силу, яка викликає прогин. Розглянемо балку, яка нагружена силою Р1. Прогин від цієї сили Δ11.
Робота сили Р1 на переміщенні Δ11 дорівнює за формулою Клайперона:
Відповідна енергія деформації:
Так як A1=U1, то Після прикладання сили Р2 точка 1 одержить додаткове переміщення Δ12. Робота сили Р1 на переміщенні Δ12 дорівнює:
В цьому виразі немає множника 1/2, так як, в процесі навантаження балки силою Р2, сила Р1 була вже прикладена і її значення не змінилось. Сила Р2 здійснює роботу на переміщенні Δ2 точки, де вона прикладена
Енергія деформації, яка відповідає навантаженню Р2 дорівнює
Повну роботу зовнішніх сил можна представити як суму трьох доданків:
Енергію деформації при спільній дії сил
А=U
Величин
Δip - переміщення точки і від сили Р. Фізичний зміст інтеграла Мора: Це робота одиничної сили на переміщенні її точки прикладення від заданого навантаження, якщо інтеграл Мора має знак «+» то напрям одиничного навантаження співпадає з напрямком шуканого переміщення, знак «-» напрямки протилежні. Послідовність визначення переміщення за допомогою інтеграла Мора: 1) Скласти рівняння згинальних моментів для кожної з ділянок від зовнішніх сил. 2) Звільнивши балку від заданого навантаження, прикласти до неї силу, яка дорівнює одиниці в тій точці де визначяється прогин і в напрямку прогину. Якщо визначяється кут повороту, то в точці потрібно прикласти одиничний безрозмірний момент. 3) Скласти рівняння згинаючих моментів від одиничної сили або від одиничного момента для кожної ділянки балки. 4) Обчислюємо суму інтегралів Мора по ділянках.
Лекція № Спосіб Верещагіна Обчислення інтегралів Мора суттєво спрощується для систем, які складаються з прямих брусів, оскільки для них епюри від одиничного навантаження обмежені прямими лініями. Обчислимо інтеграл
довільна, а від одиничної – прямолінійна.(рис. 7.4).
C – її центр ваги,
Очевидно, Тоді
Інтеграл Підставляючи це рівняння, одержимо:
Отже, якщо одна з епюр лінійна, то інтеграл Мора дорівнює добутку площі нелінійної епюри на ординату прямолінійної епюри, взятої під центром ваги епюри нелінійної. Оскільки епюра MP(x), як правило, складна– це ряд графіків різних кускових функцій, то обчислення виконують, розбиваючи епюри на ділянки так, щоб одна з епюр була обов’язково лінійна на цій ділянці, а для другої можна було б визначити площу і положення центра ваги. Загальна формула для визначення переміщення способом Верещагіна має вигляд:
Це математичний вираз правила Верещагіна: переміщення дорівнює сумі добутків площі нелінійної епюри згинальних моментів Оскільки ми розглядаємо балки постійної жорсткості, тобто EIZ=const, то її можна винести за знак суми. Обчислення інтеграла Мора за правилом Верещагіна часто називають способом перемноження епюр. При цьому епюру MP(x) називають вантажною, а
Площі епюр на відстані до їх центрів ваги
Дані для параболічних епюр вірні за умовою, що т.а. – це вершина параболи, тобто дотичне в цій точці паралельна осі балки. Практичні рекомендації щодо застосування способу Верещагіна 1. Добуток площі вантажної епюри на ординату лінійної вважається додатнім, якщо епюри розташовані по один бік від базової лінії. 2. Якщо в межах однієї силової ділянки вантажна і одинична епюри прямолінійні, то все одно, площу якої епюри брати, і на ординату якої множити. 3. Якщо в межах силової ділянки одна із епюр криволінійна, а інша ламана, то слід розбити другу епюру на ділянки, в межах яких вона лінійна. 4. Якщо вантажна епюра і одинична епюра ламані і границі їх ділянок співпадають, то треба розбити ці дві епюри на лінійні ділянки. При цьому може статися, що на одній з ділянок краще брати площу епюри Mp, а на іншій площу епюри M1. Завжди треба брати площу тієї епюри, яка в межах даної ділянки однозначна.
Mp
M1
6.Епюри, побудовані спеціально для застосування правила Верещагіна, не штрихують. 7.Іноді виявляється зручним будувати вантажну епюру у так званому розшарованому вигляді. Суть цього розшарування полягає в наступному: рівняння згинального момента M(x) являє собою складну функцію. Наприклад, для балки на рис. 7.5, для ІІІ ділянки M(x) = -Px + M – q(x-b)2/2. Замість того, щоб будувати графік цієї складної функції, для (рис. 7.5,а) перемноження епюр доцільно побудувати графіки від кожного доданку (тобто окремі епюри) (рис.7.5,б). При цьому розшаровану вантажну епюру будують по одиничній в залежності від місця зламу на одиничній епюрі.
Лекція № Лекція№ Згин Плоский згин Прямолінійні стержні, що працюють на згин називаються балками.Якщо всі зовнішні навантаження діють в одній площині, що називаються силовою, причому ця площина збігаеться з однією із головних площин балки, то має місце плоский поперечний згин.
      

Мкр=0: N=0; Q≠0; M≠0; Види опор та їх реакції 1)Затиснення або жорстке стиснення виникає 3 складові:Ma;Ra;Na.
2)Шарнірно-нерухома опора

3)Шарнірно-рухома опора Виникає тільки вертикальна реакція Ra.
Балки бувають: 1) Однопрольотні 2) Багатопрольотні 3) Консолі Визначення реакцій балки

Перевірка
Тобто Ra та Rb знайшли вірно.
При плоскому згинанні балках при навантаженні, перпендикулярному до осі балки поздовжна сила буде дорівнювати нулю. Тому в будь якому перерізі балки виникають тільки два внутрішніх зусилля: поперечна сила Q та згинальний момент М. Якщо навантаження зосереджене в головній площині стержня x y, то Q z =0; M x =0; M y =0; N=0 так як сили перпендикулярні осі балки. Залишаються:
Залишаються:
Установимо такі правила знаків для Q і М в балках: 1. Поперечна сила Q у перерізі додатна, якщо її вектори намагаються обертати частини розсіченої балки за годинниковою стрілкою.
Q > 0 Q < 0
2. Згинальний момент М у перерізі додатний, якщо він спричиняє стиснення у верхніх волокнах балки і спрямований таким чином:
M > 0 M < 0
Особливості епюр поперечних сил Q та згинальних моментів M
1. На ділянках, де немає розподільного навантаження епюри Q окреслюються прямими, паралельними базі, а епюри М в загальному випадку нахиленими прямими.
2. На ділянках, де до балок прикладене рівномірно розподілене навантаження q, епюра Q обмежується нахиленою прямою, а епюра М – квадратичною параболою. Випуклість параболі звернена в бік протилежний напряму дії навантаження q. Правило дощику або парасольки:
3. В перерізах де Q = 0, дотична до епюри М паралельна базі епюри.
4. На ділянках де Q > 0, момент зростає, де Q < 0, момент М зменшується.
5. Якщо в шарнірі, або на кінці консолі не прикладений зосереджений момент, то на епюрах моментів М=0.
6. У перерізах, де до балки прикладені зосереджені сили: а) на епюрі Q будуть стрибки на величину і в напрямку дії прикладених сил.
б) на епюрі М будуть переломи, причому вістря перелому спрямоване проти дії сили; 7. У перерізах, де до балки прикладені зосереджені моменти, на епюрі М будуть стрибки на значення цих моментів (на епюрі Q змін не буде); 8. Якщо на кінці консолі або в шарнірі прикладен зосереджений момент, то в цьому перерізі згинальний момент дорівнює зовнішньому моменту.
Епюри Q та M при зміні 1)
Q(x) =-P M(x) =-P*x
2)
Q(X) =- M(X) = 3)
Ra=Rb=
Q(X)=Ra- M(X)=
M(
4)
Q(X)=Ra
M(X)=
M(a)=
5) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |





 ;
Ha=0 з рівняння
;
Ha=0 з рівняння  Далі ми складову На і писати небудемо бо вона =0;
1)
Далі ми складову На і писати небудемо бо вона =0;
1) 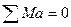
 2)
2) 
 3)Перевірка
3)Перевірка 








 y
y










 z P M
z P M 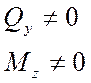 x
x
































 )=
)=  -max момент
-max момент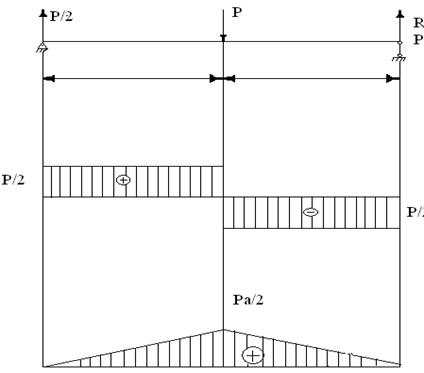 Ra=Rb=
Ra=Rb= 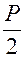

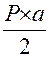


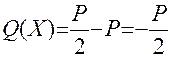

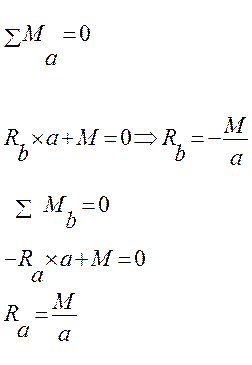







 ;
; 


 - закон Гука при згині;
- закон Гука при згині;  (добуток) – називається жорсткістю перерізу при згині
(добуток) – називається жорсткістю перерізу при згині 

 - формула Нав’є.
- формула Нав’є. - Показує, що центр ваги лежить на осі Z.
- Показує, що центр ваги лежить на осі Z. - Показує, що вісі Z та y головні центральні. Тобто вісь Z нейтральна лінія перерізу проходить через центр ваги, а осі y та z – головні центральні осі перерізу.
- Показує, що вісі Z та y головні центральні. Тобто вісь Z нейтральна лінія перерізу проходить через центр ваги, а осі y та z – головні центральні осі перерізу. змінюється лінійно по товщині балки.
змінюється лінійно по товщині балки.

 - осьовий момент опору
- осьовий момент опору 
 де
де 

 Прямокутник:
Прямокутник: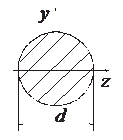 Коло:
Коло: (6-6)
(6-6)




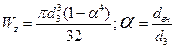
 . Далі знаходимо
. Далі знаходимо  потім
потім  .
. Розглянемо будь-яку пружну систему.
Розглянемо будь-яку пружну систему.

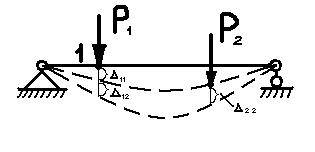 Прикладаємо далі силу Р2. До прогина Δ11 точки, де прикладена сила Р1, від цієї ж сили добавиться прогин Δ12 від сили Р2.
Прикладаємо далі силу Р2. До прогина Δ11 точки, де прикладена сила Р1, від цієї ж сили добавиться прогин Δ12 від сили Р2.

 .
. .
. .
. , A2=U2.
, A2=U2.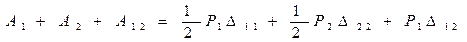
 та
та 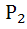 знайдемо, враховуючи, що
знайдемо, враховуючи, що  (до визначення згинальних моментів можна застосувати принцип незалежної дії сил):
(до визначення згинальних моментів можна застосувати принцип незалежної дії сил):
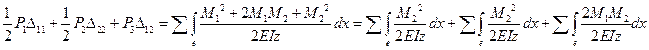


 - це одиничний момент,який викликається дією сил рівної 1(безрозмірна)
- це одиничний момент,який викликається дією сил рівної 1(безрозмірна) або
або  - Інтеграл Мора
- Інтеграл Мора у випадку, коли епюра від зовнішнього навантаження
у випадку, коли епюра від зовнішнього навантаження Позначимо:
Позначимо: - площа нелінійної епюри MP(x) від зовнішнього навантаження,
- площа нелінійної епюри MP(x) від зовнішнього навантаження, - ордината епюри від одиничного навантаження під центром ваги епюри MP(x).
- ордината епюри від одиничного навантаження під центром ваги епюри MP(x). .
.
 .
. є статичний момент площі
є статичний момент площі  .
. , тобто
, тобто  .
. (7-5)
(7-5) лінійної епюри, взяту під центром ваги нелінійної, поділеному на жорсткість перерізу EIZ при згинанні.
лінійної епюри, взяту під центром ваги нелінійної, поділеному на жорсткість перерізу EIZ при згинанні. - одиничною.
- одиничною.
 =1/2hl
=1/2hl



 5.Складні епюри розбивають на ділянки, в межах яких одна з епюр обов’язково лінійна, і беремо ординату лінійної епюри, площу – будь-якої, потім підсумовуємо їх добутки по всій довжині балки.
5.Складні епюри розбивають на ділянки, в межах яких одна з епюр обов’язково лінійна, і беремо ординату лінійної епюри, площу – будь-якої, потім підсумовуємо їх добутки по всій довжині балки.


