Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема4.Основні експлуатаційні властивості машин і механізмів.Содержание книги
Поиск на нашем сайте
Надійність,безвідмовність, довговічність, збереження, ремонтопридатність, справність, несправність, працездатність, відмова, термін служби, спрацювання, ресурс, продуктивність, відповідність показникам призначення, естетичність, ергономічность, економічність. Надійність є комплексним показником якості машин оскільки в нього входять показники: довговічність, збереження і ремонтопридатність. Ремонтопридатність показник тимчасовий. У технічно розвинених країнах він відсутній, оскільки машини, які відпрацювали свій паспортний ресурс відправляють на металобрухт. Комплексним показником надійності є коефіцієнти готовності і технічного використання. Коефіцієнт готовності – вірогідність того, що машина буде працездатна в довільний момент часу в проміжках між плановими ремонтами, окрім планованих періодів, в перебігу яких застосування машини не передбачається. У сталому режимі експлуатації коефіцієнт готовності:
Коефіцієнт технічного використання - відношення інтервалів часу перебування машини в працездатному стані, на деякий період експлуатації до суми інтервалів часу перебування машини в робочому стані,простоїв обумовлених технічним обслуговуванням і ремонтів за той же період експлуатації.
де Тсум – сумарне напрацювання всіх однакових об’єктів, експлуатованих в заданий період; Трем – сумарний час напрацювання машини у зв’язку з плановими ремонтами; Тобс – сумарний час напрацювання машини у зв’язку з плановим і неплановим технічним обслуговуванням. Вірогідність безвідмовної роботи:
де n| – числу машин які вийшли з ладу n – число машин,які безвідмовно пропрацювали до моменту часу. N – число випробованих машин. Для машин які за системою ППР підлягають капітальним ремонтам, велике зна чення має комплексний показник рівня ремонтопридатності. При аналізі надійності розраховується також решта характеристик експлуатаційної надійності. Методика обробки даних статистичних спостережень про надійність. Визначення показників надійності пов’язано з рішенням двох головних задач математичної статистики – оцінка невідомих параметрів вибірки (множина випадкових даних про напрацювання на відмову) та перевірки статистичних гіпотез відносно законів розподілу ймовірності значень напрацювання на відмову. Обробка результатів дослідження надійності дозволяє вирахувати числові характеристики емпіричного розподілу (вибірки) ймовірності значень напрацювання на відмову, які називаються статистичними оцінками (емпіричними або вибірковими характеристиками), які аналогічні числовим характеристикам ВВ (випадкової величини – величини напрацювання на відмову): математичне очікування, дисперсія, початкові та центральні моменти різних порядків. Кожній числовій характеристиці ВВ відповідає її статична аналогія. Математичним очікування де n – число реалізаціїї (об’єм вибірки) випадкової величини;
При необмеженому збільшенні n статистичне середнє наближується (зводиться за вірогіднісьтю) до математичного очікування. Зі збільшенням об’єму вибірки n зростає довірча вірогідність (надійність) Статистична оцінка дисперсії ВВ може визначатися за формулою:
Аналогічно визначаємо статистичні початкові
При збільшенні n всі статистичні характеристики ( При великих об’ємах вибірки n розрахована характеристика, за формулами(4.4)-(4.6) ускладнюється, тому отримані емпіричні данні представляють у виді статистичного ряду. Для цього весь діапазон значень випадкової величини розбивають на інтервали, кількість котрих в залежності від об’єму вибірки, повинно бути не менше 5-6 та не більше 10-12. Примірна величина інтервалу
де Кількість інтервалів При цьому інтервали мають однкову довжину. Число значень Розглянемо формування статистичного ряду на прикладі 300 реалізацій випадкових значень
Таблиця 4.2
Можна прийняти
Для кожного інтервалу підраховується
Накопичена частота Як видно із табл. 4,2 можуть бути знайдені статистичні оцінки математичного очікування та дисперсії випадкової величини. Для угруповування данних статистичні числові храктеристики виражаються слідуючими формулами:
Наведені формули аналогічні формулам для дискретних ВВ, тільки з тією різницею, що замість вірогідності В прикладі, що розглядається
Після об’єднання двух або деяких останніх інтервалів з малою частотою попадання значень ВВ кількість розрідів
При необхідності можуть бути розраховані також початкові та центральні моменти інших порядків. Для наочного уявлення про емпіричний розподіл значень будується гістограма (ступінчаста діаграма) емпіричної щільності розподілення випадкової величини (рис. 4.1). По осі абсцис відкладаємо інтервали (розряди) Висоти прямокутників пропорційні відповідним висотам та рівні емпіричної щільності вірогідності
Рисунок 4.1. Ступінчаста діаграма емпіричної щільності вірогідності
Рис. 4.2. Гістограма статистичного розподілу щільності ймовірності ВВ при експоненційному законі
Якщо вид теоретичної функції розподілення ВВ заздалегідь відомий, то зовнішній вид діаграми гістограми може слугувати основою для підбору тої або іншої теоретичної диференційної функції розподілення (щільності розподілення), описують отримане емпіричне розподілення. Сумістивши гістограму(рис.4.1) з теоретичною кривою розподілення можна прийняти гіпотезу про те, що ВВ підкоряється нормальному або іншому закону розподілення ймовірності значень ВВ. Сумістивши гістограму, побудовану по даним табл. 4.2 (рис. 4.2), з графіком зміни вірогідності безвідмовної роботи об’єкту при експененційному законі розподілення спрацювання між відмовами або до відмови, можно допустити, що випадкові значення часу роботи промислового комплексу між відмовами підкоряються експоненційному закону розподілення. Дана пропозиція доводиться тим фактом, що величина коефіцієнта варіації ВВ
Таблиця 4.3
Розподіл щільності вірогідності випадкової величини, що підкорюється експоненційному закону розподілення описується виразом
Прийняв в якості математичного очікування його статистичну оцінку Обчислені значення щільності вірогідності на границі інтервалів зведені у табл.9.3. На гістограмі (див.рис.4.2) по даним табл. 4.3 побудована вирівнююча крива розподілення, яка представляє собою графік теоретичної функції При підборі теоретичної кривої розподілення між нею та статичним розподіленням неминучі деякі розходження. При цьому необхідно знати, пояснюються ці відхиленні тільки випадковими обставинами, зв’язаними з обмеженим числом дослідних даних, або вони являються суттевими та пов’язані з тим, що підібрана крива погано вирівнює дане статичне розподілення. Ступінь відповідності між запропонованою гіпотезою зі статистичним матеріалом встановлюється за допомогою критерія згоди. Найбільш розповсюдженим являється критерій К. Пірсона
де Для експоненціального закону розподілу
Значення рі наведені у табл. 4.3. За формулою(9.11) та даним табл. 4.2 та 4.3
Число степенів свободи r=k – s, де k – число інтервалів групування випадкової величини; s – число незалежних умов (зв’язків), накладених на частоти Так, наприклад для експоненціального закону розподілення.
Таблиця 4.4
Користуючись табл. 4.4, можна для отриманих значень Якщо отримана вірогідність В нашому прикладі Згідно до табл. 4.4 для =10,2 та Таким чином, в результаті обробки вихідної статичної інформації про безвідмовність промислового комплексу розподілена у вигляді статистичного ряду (див. табл. 4.2), встановлені: середня напрацювання на відмову комплексу:
вид закону розподілення неперервної величини t:
аналітичний вираз для визначення вірогідності безвідмовної роботи комплексу: де t – текучий період комплексу з моменту його включення. Аналогічна статистична обробка статистичних даних справедлива і при інших законах розподілення безперервних ВВ. Так, наприклад при перевірці гіпотези про відповідність дослідного розподілу розрахунок значень щільності вірогідності ( Заздалегідь на основі статичного ряду, складені за формою табл.9.2, повинні бути розраховані статистичні числові характеристики
Література [6;9;13] Індивідуальне завдання. Для механізму (за отриманим варіантом) та даними статистичних спостережень (допускається створення масиву даних шляхом генерації випадкових чисел) визначити параметри його експлуатаційних властивостей.
ПЗ № 5. Тема. Вибір технічних засобів контролю та діагностики працездатності машин під час експлуатації. Основні питання теми: Технічні засоби контролю та діагностики технічного стану під час експлуатації. Задачі технічної діагностики машин. Методи та технічні засоби діагностики. Вибір діагностичних параметрів. Алгоритми пошуку пошкоджень та дефектів. Побудова систем технічної діагностики. Зовнішній огляд. Методи виявлення тріщин та внутрішніх дефектів деталей машин. Способи та періодичність діагностування. Метрологічне забезпечення експлуатації машин.
Інформаційні матеріали. Технічна діагностика - комплекс заходів по оцінці стану машини без їх розбирання, що дозволяє оцінити стан конкретної машини або її окремих складальних одиниць в поточному часі, тобто встановити її справність або несправність, а також її основні експлуатаційні показники, технічний стан окремих складальних одиниць і деталей потреба в обслуговуванні і ремонті, їх ресурс. Застосування технічної діагностики забезпечує підвищення ефективності використання технічного обслуговування і ремонту машин. а також зростання їх експлуатаційної надійності. Ефективність технічного діагностування досягається за рахунок: точного встановлення фактичного технічного стану машин і устаткування і його подальшого прогнозування. Внаслідок чого підвищується безвідмовність; знижується витрата запасних частин; скорочуються терміни робіт по технічному обслуговуванню і ремонту, зменшується трудомісткість технічного обслуговування і ремонту за рахунок організації цих робіт по фактичній потребі(по технічному стану).Діагностичні ознаки у різних машин, вузлів, складальних одиниці і деталей - різні - (рівень шуму, вібрація, знос, деформація деталей, зазори в з'єднаннях і т. д.). Перед створенням системи діагностики повинен бути встановлений зв'язок між зміною технічного стану об'єкту діагностування і діагностичними ознаками. Методи і засоби виявлення дефектів і технічної діагностики: зовнішній огляд механічних пошкоджень з подальшою дефектоскопією, ультразвуковий, віброакустичний, вимірювання тиску в гідросистемах за допомогою датчиків тиску; вимірювання температури нагріву підшипників і робочих рідин термопарами і терморезисторами, вимірювання в автоматичному режимі класу чистоти робочих рідин за допомогою приладу ФС-151. Для вимірювання зносу направляючих металоріжучих верстатів застосовуються методи: штучних баз і поверхневої активації. Для виявлення тріщин в деталях машин застосовуються методи: капілярний, капіллярно-люмінісцетний і магнітної дефектоскопії. Для виявлення внутрішніх дефектів в деталях застосовують методи: рентгеноскопічний і ультразвуковий. У багато машин вже на стадії проектування, в сьогоднішній день, закладаються в складальні одиниці і вузли датчики, які постійно падають сигнали в блок прийому інформації про технічний стан механізму. Прогнозування залишкового ресурсу. В процесі експлуатації машин їх технічний стан постійно змінюється. Визначити технічний стан устаткування в майбутньому можна шляхом прогнозування, яке при відомих нормативних значеннях діагностичних параметрів дозволяє визначити залишковий ресурс машини. Залишковий ресурс складальних одиниць визначають по тих параметрах, які є вирішальними при визначенні доцільності їх експлуатації для проведення подальшого ремонту. Оскільки для редукторів і коробок швидкостей такими параметрами можуть бути параметри віброакустичного сигналу. В даний час технічна діагностика стала найважливішим елементом планово-попереджувальної системи ТО і ремонту машин. Розробляються модульні системи діагностування і діагностичні станції, а також включення засобів діагностики в конструкцію машин. Література [6;9;13;14.] Контрольні питання. 1. Дайте визначення технічної діагностики і її завдання. 2. Опишіть призначення технічної діагностики. 3. Перерахуйте основні діагностичні ознаки різних машин. 4. Назвіть основні методи виявлення дефектів. 5. Опишіть основні засоби виявлення дефектів. 6. Прогнозування залишкового ресурсу машин і основні методи технічної діагностики. 7. Перспективи розвитку діагностики. Індивідуальне завдання. Для механізму (за отриманим варіантом) запропонувати методи і технічні засоби діагностики його технічного стану.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.147 (0.012 с.) |


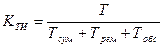

 ,
, випадкової величини
випадкової величини  , являється його статистична оцінка
, являється його статистична оцінка  , яка представляє собою середнє арифметичне (статистичне середнє) значення отриманих в результаті випробовувань реалізації ВВ:
, яка представляє собою середнє арифметичне (статистичне середнє) значення отриманих в результаті випробовувань реалізації ВВ: 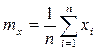 ,
, – і- я реалізація (значення) випадкової величини
– і- я реалізація (значення) випадкової величини  статистичного середнього та знижується величина відносної помилки
статистичного середнього та знижується величина відносної помилки  .
.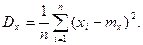
 та центральні
та центральні  моменти різного порядку:
моменти різного порядку: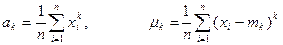 ,
, ,
,  ,
,  ) зводитимуться за вірогіднісьтю до відповідних математичних характеристик.
) зводитимуться за вірогіднісьтю до відповідних математичних характеристик. визначається за формулою:
визначається за формулою:
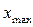 ,
,  – відповідне максимальне та мінімальне значення досліджуємої величини; n – кількість отриманих реалізацією випадкової величини (об’єм вибірки).
– відповідне максимальне та мінімальне значення досліджуємої величини; n – кількість отриманих реалізацією випадкової величини (об’єм вибірки). угруповувань випадкової величини знаходиться з виразу:
угруповувань випадкової величини знаходиться з виразу: 
 випадкової величини
випадкової величини  часу роботи між відмовами промислового комплексу, серед яких
часу роботи між відмовами промислового комплексу, серед яких 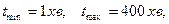 приймаємо
приймаємо  . В цьому випадку
. В цьому випадку



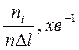
 тоді
тоді
 - число значень випадкової величини, які знаходяться в заданому інтервалі;
- число значень випадкової величини, які знаходяться в заданому інтервалі;  - частота (статистична вірогідність);
- частота (статистична вірогідність);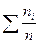 - накопичена частота;
- накопичена частота; 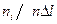 - імперична щільність верогідності,
- імперична щільність верогідності,  . Дані заносяться в таблицю 4.2.
. Дані заносяться в таблицю 4.2. при
при  для всіх інтервалів повинна дорівнювати 1.що слугує для перевірки вірності обчисленних частот для кожного інтервалу.
для всіх інтервалів повинна дорівнювати 1.що слугує для перевірки вірності обчисленних частот для кожного інтервалу.

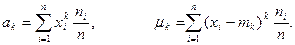
 фігурують частоти
фігурують частоти  - статистичне середнє
- статистичне середнє  , замість чисел можливість значень випадкової величини n – кількість розрядів
, замість чисел можливість значень випадкової величини n – кількість розрядів  -х розрядів (середини інтервалів
-х розрядів (середини інтервалів  )
) 
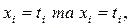 тому
тому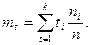
 , а значення
, а значення  , та складають:
, та складають:  хв,
хв, 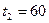 хв,
хв,  хв,...,
хв,...,  хв. тоді статистичне середнє математичне очікування:
хв. тоді статистичне середнє математичне очікування: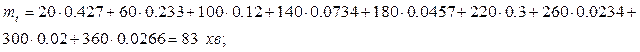 Статистична середня дисперсія:
Статистична середня дисперсія: Статистичне середнє квадратичне відхилення та коефіцієнт варіації ВВ складуть:
Статистичне середнє квадратичне відхилення та коефіцієнт варіації ВВ складуть: хв;
хв; 
 t для кожного інтервалу.
t для кожного інтервалу.

 .
.

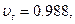 дуже близька до одиниці, а для експоненціального закону розподілення
дуже близька до одиниці, а для експоненціального закону розподілення 




 хв, отримаємо
хв, отримаємо 
 , котра, зберігаючи в основному вагомі особливості статистичного розподілення, вільна від випадкових невірних ходів гістограми.
, котра, зберігаючи в основному вагомі особливості статистичного розподілення, вільна від випадкових невірних ходів гістограми. величина якого розраховуються за формулою
величина якого розраховуються за формулою ,
, – число інтервалів групування випадкової величини; nі – число значень випадкової величини; в і – му інтервалі; n – загальне число отриманих значень випадкової величини; рі – теоретична вірогідність потрапляння випадкової t в і – й інтервал. Теоретична вірогідність потрапляння випадкової величини t в і – й інтервал дорівнює приросту функції розподілу на цьому інтервалі:
– число інтервалів групування випадкової величини; nі – число значень випадкової величини; в і – му інтервалі; n – загальне число отриманих значень випадкової величини; рі – теоретична вірогідність потрапляння випадкової t в і – й інтервал. Теоретична вірогідність потрапляння випадкової величини t в і – й інтервал дорівнює приросту функції розподілу на цьому інтервалі: 
 , тому
, тому 

 розподілення
розподілення  визначається за формулою:
визначається за формулою: . Такими зв’язками являється умова
. Такими зв’язками являється умова 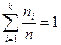 , а також число l невідомих параметрів теоретичного розподілу, визначається за даними вибірки. Умова
, а також число l невідомих параметрів теоретичного розподілу, визначається за даними вибірки. Умова 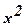 при р
при р
 ,
,  ; для нормального розподілу
; для нормального розподілу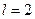 ,
,  та
та 
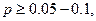 то зазавичай враховуємо, що дослідні дані не заперечують прийнятому теоретичному закону розподіленню значень випадкової величини.
то зазавичай враховуємо, що дослідні дані не заперечують прийнятому теоретичному закону розподіленню значень випадкової величини. , тому
, тому 
 ,
,  . Отримана вірогідність не являється малою, тому гіпотезу щодо випадкові величини значень часу безвідмовної роботи промислового комплексу розподілена за експоненційним законам, можна зарахувати за правдиву.
. Отримана вірогідність не являється малою, тому гіпотезу щодо випадкові величини значень часу безвідмовної роботи промислового комплексу розподілена за експоненційним законам, можна зарахувати за правдиву. хв;
хв;
 ,
, ) на межі інтервалів групування випадкової величини та теоретичної величини потрапляння ВВ у
) на межі інтервалів групування випадкової величини та теоретичної величини потрапляння ВВ у  ті інтервали(див. табл. 4.3) проводиться за формулами (4.27) та (4.28). При цьому необхідно пам’ятати, що вірогідність потрапляння випадкової величини t в розглянутий інтервал рівна приросту функції розподілення
ті інтервали(див. табл. 4.3) проводиться за формулами (4.27) та (4.28). При цьому необхідно пам’ятати, що вірогідність потрапляння випадкової величини t в розглянутий інтервал рівна приросту функції розподілення 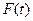 на цьому інтервалі, а саме
на цьому інтервалі, а саме