
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виконання прикладу завдання по першій лабораторній роботіСтр 1 из 4Следующая ⇒
3.1. По умові завдання необхідно визначити числові значення показників надійності приводних клинових пасів (колінчастих валів) по результатах випробувань 40а однотипних зразків. Так клинові паси являються виробами, що не ремонтуються, тому основними показниками їх надійності є диференційна f(t) та інтегральна F(t) функції розподілу напрацювання цих виробів до першого відказу, ймовірність безвідказної роботи Р(t), середнє напрацювання до першого відказу Ці ж показники безвідказності визначаються і для виробу, що ремонтується (колінчастого валу) по результатах спостережень напрацювань до першого відказу (додатки 2 та 3). Числові значення показників надійності визначають по результатах спостережень за випробуваннями однотипних виробів в заданих умовах, фіксуючи напрацювання окремих виробів до першого відказу в годинах (мото-год, для колінчастих валів) роботи під навантаженням. Результати спостережень подають у вигляді інтервального статистичного ряду розподілу напрацювання виробів до першого відказу, які і розміщені в додатках 1 та 2 Для вказаного вище зразкового завдання часткові інтервали значень напрацювання Ті приймаються по варіанту 11 (додаток 1), а значення частот mi відказів пасів по і-х частових інтервалах (додаток 3). У випадку колінчастих валів для інтервального ряду (додаток 2 – варіант 1), а для значень частот (додаток 3 – варіант 6). Інтервальний статистичний ряд емпіричного розподілу напрацювання Т1 для заданих умов наведений в табл. 3.1. В цій же таблиці вказані значення частостей (емпіричних імовірностей) Таблиця 3.1. Інтервальний статистичний ряд емпіричного розподілу клинових пасів до першого відказу
3.2. Дані табл. 3.1. використовуються для побудови графіків, які наочно характеризують емпіричні розподіли випадкових величин – гістограми, полігона та інтегральної функції емпіричного розподілу напрацювання.
Для побудови гістограми по горизонтальній осі графіка відкладають значення, які відповідають границям часткових інтервалів, а на вертикальній – частоти та частості по окремих інтервалах. Далі будуються прямокутники, основи яких лежать на горизонтальній осі координат і дорівнюють значенням часткових інтервалів, а висоти дорівнюють частотам або частостям відповідних інтервалів (табл. 3.1.). В результаті одержуємо ступінчастий багатокутник або гістограму. Якщо з’єднати прямими лініями середини верхніх горизонтальних сторін прямокутників гістограми, то одержимо полігон розподілу у вигляді ламаної лінії. Приклад побудови гістограми та полігона розподілу напрацювання клинових пасів до першого відказу наведений на рис. 3.1. На рис. 3.2 показані диференційні функції (гістограма та полігон частостей розподілу напрацювання колінчастих валів двигуна “Д-65Н” до першого відказу (додаток – 2 – варіант 1; додаток 3 – варіант 6) у випадку зміщення інтервального ряду.
Найбільш загальною характеристикою розподілу як дискретних так і неперервних випадкових величин є інтегральна функція розподілу F(T), яка визначає ймовірність тої події, що випадкова величина Т буде менша або рівна наперед заданому значенню t, тобто F(T) = Р(Т£ t). Емпірична інтегральна функція розподілу визначає частість (дослідну ймовірність) події Т£ t, а теоретична інтегральна функція розподілу – ймовірність даної події. Функція розподілу F(T) може бути задана аналітично або представлена у вигляді графіка (рис. 3.3). На рис. 3.3 наведений приклад побудови емпіричних інтегральних функцій напрацювання клинових пасів до відказу та напрацювання колінчастих валів до першого відказу (див. рис. 3.2, для колінчастих валів – вихідні дані: додаток 2 – варіант 1, додаток 3 – варіант 6). У випадку дослідження напрацювання колінчастих валів до першого відказу (рис. 3.3, крива 2).
Таким чином, початкова точка ломаної лінії лежить на осі абсцис і відповідає значенню Т1 = 0,5 тис. мото-г.
Частість
Рис. 3.3 Експериментальні функції розподілу напрацювання клинових пасів та колінчастих валів до першого відказу.
3.3. Числові значення статистичних характеристик розподілу випадкової величини, таких, як середнє арифметичне значення
де Тсі – значення середини і-го інтервалу; і – кількість інтервалів інтервального ряду;
Програми розрахунку Таблиця 3.2 Програма розрахунку середнього значення 10 REM 15 DIN T(50), M(50) 20 S = 0 30 PRINT ROL INTERVALOW – N1” 40 INPUT NL 50 PRINT “OBEM VIBORKI NO” 60 INPUT NO 70 FOR J=1 TO N1 80 PRINT “SREDN I KOL “J” – GO INTERVALA” 90 INPUT T(J), N(J) 100 S=S+T(J) M(J) 110 NEXT J 120 TO=S/NO 130 PRINT TO
Таблиця 3.3 Програма розрахунку вибіркового значення середнього квадратичного відхилення 10 REM-OHREDEL SKW 20 DIN T(50), M(50) 25 S = 0 30 PRINT ROL INTERVALOW – N1” 40 INPUT NL 50 PRINT “OBEM VIBORKI NO” 60 INPUT NO 70 PRINT-“SREDNEE –TO” 80 INPUT TO 90 FOR J=1 TO N1 100 PRINT “SREDN I KOL “J” – GO INTERVALA 110 INPUT T(J), N(J) 120 S=S+(T(J)-TO) 130 NEXT J 140 A=SQR (S/NO) 150 PRINT A 160 END
Для розрахунку значень Таблиця 3.4 Визначення значень
В дві перші графи табл. 3.4 переписують значення з 1-го та 2-го рядків табл. 3.1. В третій графі табл. 3.4 роблять прочерк проти найбільшого значення частоти mi (в нашому прикладі це 17), а в четвертій графі – три прочерку: проти прочерку в тертій графі та зверху і знизу від нього. Далі в третій графі виконують послідовно додавання наростаючим підсумком значень mi по часткових інтервалах, починаючи від першого значення до прочерку та від останнього значення до прочерку. Одержані суми складають і підраховують значення двох допоміжних коефіцієнтів К1 та Л1. Аналогічно одержують значення допоміжних коефіцієнтів К2 та Л2 по четвертій графі. Потім підраховуються допоміжні коефіцієнти М1 = К1- Л1 і М2 = К1+ Л1 + 2К2+ 2Л2 потім визначають середнє арифметичне значення напрацювання клинових пасів до першого відказу
де Тс max – значення середини часткового інтервалу з максимальною частотою відказів, напроти якого зроблений прочерк в третій графі;
Результати розрахунків:
Ступінь розсіювання випадкової величини визначається безрозмірною числовою характеристикою – коефіцієнтом варіації:
де tзм - величина зміщення зони розсіювання Т1 відносно нульового значення Зміщення необхідно приймати чисельно рівним нижній границі першого часткового інтервалу. З таблиць рядів розподілу випадкових величин в наших прикладах у випадку клинових пасів tзм=0, а у випадку колінчастих валів tзм=0,5 тис. мото-г. так у випадку клинових пасів коефіцієнт варіації підраховується по рівнянню:
Даний безрозмірний коефіцієнт не тільки використовується як відносна характеристика ступеню розсіювання випадкової величини відносно середнього значення, але і для орієнтованого вибору теоретичного закону розподілу (ТЗР) випадкової величини. Стосовно до завдання, що розглядається, при n £ 0,33 – закон розподілу вибирається нормальний, а при n > 0,33 – закон розподілу Вейбулла. Оскільки в першому прикладі значення n < 0,33, приймаємо для подальших розрахунків нормальний закон розподілу напрацювання клинових пасів до першого відказу. Цей орієнтований висновок необхідно в подальшому перевірити за допомогою критерію О.М.Колмогорова [1, 2, 3, 4].
3.4. Статистична оцінка ймовірності безвідказного напрацювання
де N – число виробів с початку випробувань (в розглянутому завданні N = 40);
N(tі) – кількість робото здатних виробів до початку і-го часткового інтервалу Вихідні дані для підрахунків та їх результати зводять в табл. 3.5 Таблиця 3.5. Визначення статистичних оцінок
3.5. Графік зміни дослідної ймовірності безвідказної роботи Приклад побудови графіка показаний на рис. 3.4. Між показниками ймовірності безвідказної роботи виробу та інтегральною функцією розподілу напрацювання до першого відказу існує взаємозв’язок, обумовлений рівнянням
Рис. 3.4. Емпірична та теоретична інтегральна функції розподілу напрацювання клинових пасів до першого відказу та ймовірність безвідказної роботи пасів по даних випробувань на надійність.
Лабораторна робота №2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.51.117 (0.058 с.) |
 , інтенсивність відказів l(t).
, інтенсивність відказів l(t). та накопичених частостей
та накопичених частостей  по окремих інтервалах. Сума частот Smi по всіх інтервалах повинна бути рівна N, тобто 40, а сума накопичених частостей
по окремих інтервалах. Сума частот Smi по всіх інтервалах повинна бути рівна N, тобто 40, а сума накопичених частостей 
 для Ті£ 0,5 тис. мото-г.
для Ті£ 0,5 тис. мото-г. для значень Т1£ 1,5 тис. мото-г.; в результаті визначається друга точка ломаної лінії. яку відрізками прямої з’єднують з початковою та третьою точкою, яка відповідає верхній границі інтервалу (S
для значень Т1£ 1,5 тис. мото-г.; в результаті визначається друга точка ломаної лінії. яку відрізками прямої з’єднують з початковою та третьою точкою, яка відповідає верхній границі інтервалу (S  для Т1£ 2,5 тис. мото-г.). Так, переходячи послідовно від одного інтервалу до другого, поступово будують графік емпіричної функції розподілу Т1, остання точка якої відповідає
для Т1£ 2,5 тис. мото-г.). Так, переходячи послідовно від одного інтервалу до другого, поступово будують графік емпіричної функції розподілу Т1, остання точка якої відповідає
 для Ті£ 6, 5 тис. мото-г.
для Ті£ 6, 5 тис. мото-г. , вибіркове середнє квадратичне відхилення
, вибіркове середнє квадратичне відхилення  підраховують по слідуючи формулах:
підраховують по слідуючи формулах: ,
,  ,,(3.1)
,,(3.1) - значення частостей (досліджених ймовірностей) по кожному і-му інтервалу.
- значення частостей (досліджених ймовірностей) по кожному і-му інтервалу. та
та 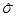 на мові Бейсик наведені в табл. 3.2 та 3.3.
на мові Бейсик наведені в табл. 3.2 та 3.3.
 2 M(J)
2 M(J)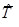 та
та  ; (3.2)
; (3.2) (3.3)
(3.3) значення напрацювання в границях часткового інтервалу (в нашому прикладі
значення напрацювання в границях часткового інтервалу (в нашому прикладі  г).
г).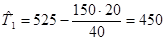 г,
г,
 , (3.4)
, (3.4)
 та інтенсивності відказів
та інтенсивності відказів  клинових пасів для і-х часткових інтервалів підраховують в наступних рівняннях:
клинових пасів для і-х часткових інтервалів підраховують в наступних рівняннях: , (3.5)
, (3.5)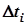 - значення напрацювання в частковому інтервалі (у кожному прикладі
- значення напрацювання в частковому інтервалі (у кожному прикладі  = 150 г.)
= 150 г.) та
та 

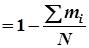 (3.6)
(3.6)


