Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический анализ механизмаСодержание книги
Поиск на нашем сайте
Синтез механизма Планы положений механизма строим в масштабе:
Строим 12 положений механизма (начиная с 0, согласно заданию), а также дополнительно те положения механизма, при которых скорость выходного звена равняется нулю. 2.2. Построение планов скоростей Находи скорость точки А:
Находим скорость точки В:
Находим угловую скорость кривошипа:
Решаем уравнение графически. Выбираем масштабный коэффициент плана скоростей:
Находим скорость точки D:
Находим скорость точки E:
Находим скорости точек и угловые скорости звеньев:
Строим планы скоростей, и результаты расчетов сводим в таблицу: Табл. 2.1
2.3. Построение плана ускорений для 2-го положения Находим ускорение точки B:
Принимаем масштабный коэффициент плана ускорений:
Находим ускорение точки С:
Используя условия пропорциональности одноименных отрезков плана ускорений и плана механизма находим положение точек D и Находим ускорение точки E:
Решаем уравнение графически. Находим ускорение точек и угловые ускорения звеньев:
Динамическое исследование основного механизма Динамическая модель машинного агрегата При исследовании движения машины реальную схему заменяют динамической моделью. Одна и та же машина может быть представлена различными динамическими моделями в зависимости от задач исследования. Простейшая динамическая модель машины с одной степенью свободы, недеформируемыми звеньями и приводом от кривошипа представляет собой одно-массовую систему, в которой начальное звено (кривошип) обладает приведенным моментом инерции Рис. 3.1. Динамическая модель механизма. Величины Приведение внешних сил и построение графика приведенного момента сил сопротивления Условием приведения внешних сил является равенство мощностей приведенного момента сил и суммы мощностей активных внешних сил, действующих на звенья механизма. На основании этого условия, проведенный момент сил определяется выражением:
Где
Для нашего механизма уравнения приведенного момента сил сопротивления примет вид:
Но учитывая то, что
Результаты вычисления приведенного момента сил сопротивления сводим в таблицу 3.1. График приведенного момента сил сопротивления строим в масштабах:
Табл. 3.1.
Построение графика сил сопротивления Работа сил сопротивления определяется выражением:
Для построения графика При графическом интегрировании в каждом интервале графика Масштабный коэффициент графика:
Где Н – расстояние точки P до начала координат О графика Для удобства дальнейших вычислений принимаем целое значения масштабного коэффициента Для
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.235.107 (0.006 с.) |





 ;
; ;
;

 м/с
м/с м/с
м/с ;
;


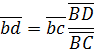
 ;
; ;
; 

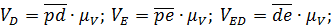
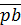
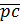
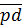

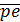
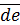










 ,
,  ;
; 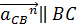 направлено от C к B;
направлено от C к B; м/
м/  ,
, на плане ускорений.
на плане ускорений.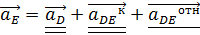
 ,
,  ;
; 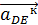 –согласно правилу векторного умножения
–согласно правилу векторного умножения м/
м/ 



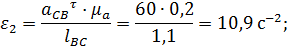
 и на который действует приведенный момент сил
и на который действует приведенный момент сил 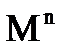 .
. динамической модели совпадала с обобщенной координатой механизма. Это позволяет исследовать закон движения только одного звена. Определение закона движения остальных звеньев производится методами кинематического анализа.
динамической модели совпадала с обобщенной координатой механизма. Это позволяет исследовать закон движения только одного звена. Определение закона движения остальных звеньев производится методами кинематического анализа.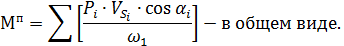
 – активная сила, приложенная к звену i;
– активная сила, приложенная к звену i; – скорость точки приложения силы;
– скорость точки приложения силы; – угол давления между векторами силы
– угол давления между векторами силы 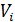 ;
; – угловая скорость начального звена.
– угловая скорость начального звена.
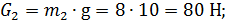

 (менее 1 %) уравнение преобразуем к виду:
(менее 1 %) уравнение преобразуем к виду: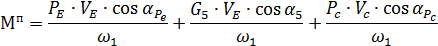





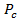


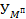

 нужно проинтегрировать график
нужно проинтегрировать график 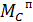 .
. представляет среднее значение в данном интервале. Эти средние значения
представляет среднее значение в данном интервале. Эти средние значения  и получаем точки. Из точки P проводим прямые. Параллельно этим прямым на графике
и получаем точки. Из точки P проводим прямые. Параллельно этим прямым на графике 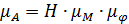
 и вычисляем полюсное расстояние Н:
и вычисляем полюсное расстояние Н: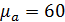 Дж/мм
Дж/мм