Лабораторная работа №3. Программирование циклических алгоритмов

Цель работы: закрепить практические навыки работы с системой Borland Pascal, научиться правильно использовать различные операторы циклов; научиться составлять программы решения задач с использованием циклических структур.

Общие сведения

Алгоритм называется циклическим, если он содержит многократное выполнение одних и тех же операторов при различных значениях промежуточных данных. Число повторений этих операторов может быть задано в явной (цикл с известным заранее числом повторений) или неявной (цикл с неизвестным заранее числом повторений) форме.

Операторы цикла

Цикл с параметром

Оператор цикла применяется при выполнении расчетов или других действий, повторяющихся определенное количество раз. Оператор имеет вид:

For i:= N1 To N2 Do "оператор";

либо

For i:= N1 DownTo N2 Do "оператор";

Здесь i - параметр цикла (переменная порядкового типа),

N1, N2 - начальное и конечное значения параметра цикла i.

N1, N2 могут быть константами, переменными или выражениями порядкового типа.

Напомним, что "оператор" может иметь вид: Begin "операторы" end;

В случае связки "To" цикл выполняется при условии N1 <= N2 и происходит с единичным возрастанием параметра цикла i от N1 до N2. В случае связки DownTo цикл выполняется при условии N1 >= N2 и происходит с единичным уменьшением параметра цикла i от N1 до N2.

В операторе цикла не разрешается присваивать параметру цикла какое-либо значение.

После окончания цикла значение параметра цикла "i" неопределенно.

Оператор цикла часто применяется для суммирования значений некоторой последовательности чисел или значений функции при известном числе операций суммирования. Напомним некоторые определения, связанные с расчетом суммы последовательности.

Сумма членов последовательности величин

a₁, a₂, a₃,..., a_n

называется конечной суммой

S_n = a₁ + a₂ + a₃+... + a_n

Для некоторых последовательностей известны формулы расчета конечных сумм, например:

при a_n = a_n-1 + d; S_n = (a₁ + a_n)*n/2; - арифметическая прогрессия,

при a_n = a_n-1 * q; S_n= (a₁ - a_n*q)/(1-q); - геометрическая прогрессия,

где d и q - постоянные числа.

Здесь N-ый член последовательности выражается через (N-1)-ый член. Такие зависимости называются реккурентными.

Конечная сумма последовательности может быть неизвестна, тогда для ее расчета применяется алгоритм суммирования членов последовательности в цикле от 1 до N. Приведем пример расчета конечной суммы последовательности: 12 + 32 + 52 +... + (2*N-1)₂; S_n = N*(4*N₂-1)/3;

PROGRAM SUM_K; { расчет конечной суммы }var a, S, Sn, i, N: word;Begin write('Введите число членов суммы N='); readln(N); S:= 0; For i:= 1 to N do begin { цикл суммирования } a:= Sqr(2*i-1); S:= S+a end; Sn:= N*(4*N*N-1) div 3; Writeln('Конечная сумма S=', S:10:2); Writeln('Расчет конечной суммы по формуле Sn=', Sn:10:2); Writeln('Нажми Enter'); ReadLn End.

В некоторых случаях "N"-ый член последовательности определяется через сумму предыдущих членов, например,

a_n= p*S_n-1,

тогда

S_n= S_n-1 + a_n = S_n-1*(1+р),

и конечную сумму можно рассчитать по формуле:

S_n = S₀*(1+p)N,

где "S₀" - начальная сумма.

Рассмотрим программу вычисления конечной суммы денежного вклада в банк через N месяцев при ежемесячной процентной ставке "pr" (5% cоответствует pr=5).

PROGRAM VKLAD; { расчет конечной суммы вклада в банк }var S, Sn, pr: Real; i, N: Integer;Begin Write('Введите начальную сумму вклада S='); readln(S); Write('Введите процент по вкладу pr='); readln(pr); Write('Введите количество месяцев вклада N='); readln(N); For i:= 1 to N do S:= S*(1+pr/100); { цикл произведений } Writeln('Конечная сумма вклада S=', S:10:2); { Оператор для расчета "Sn" напишите самостоятельно } Writeln('Расчет конечной суммы вклада по формуле Sn=', Sn:10:2); Writeln('Нажмите Enter'); readln End.

Часто применяются вложенные операторы цикла. Например, если необходимо провести все варианты расчета при изменении нескольких параметров в заданных диапазонах.

Составим программу расчета функции y = A*sin(x) - cos(x)/A; при изменении аргумента "x" в диапазоне от 0 до Pi с шагом Pi/100 и при изменении параметра "A" в диапазоне от 1 до 3 с шагом 0.5.

Program tabl;var y, x, a, dx: real; i, j: integer;Begin Writeln(' Расчет по формуле: y=A*sin(x)-cos(x)/A; '); Writeln('--------------------------------------------------'); Writeln('| X | A=1.0 | A=1.5 | A=2.0 | A=2.5 | A=3.0 |'); Writeln('--------------------------------------------------'); dx:= pi/100; for i:= 0 to 100 do begin { внешний цикл изменения аргумента "X" } x:= dx*i; Write(x:8:4); for j:= 1 to 5 do begin{ вложеннный цикл изменения параметра "A" } A:= 0.5*(j+1); y:= A*sin(x)-cos(x)/A; Write(y:8:4) end; Writeln; {перевод курсора на новую строчку} if ((i+1) mod 20) = 0 then readln{задержка прокрутки экрана до нажатия Enter} end; readln;End.

Операторы цикла с условием

В Турбо-Паскале применяются два оператора цикла с условием:

While "условие" DO "оператор";

- цикл с предусловием: проверка условия перед каждым выполнением "оператора",

Repeat "операторы" Until "условие";

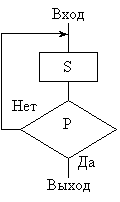
- цикл с постусловием: проверка условия после каждого выполнения "операторов".

Здесь "условие" - выражение логического типа (Boolean).

Схема выполнения операторов имеет вид:

Цикл WHILE	Цикл REPEAT

 

В цикле While "оператор" выполняется если условие верно (True), если условие ложно (False), то цикл заканчивается, т. е. цикл While повторяется пока выполняется условие. Цикл While начинается проверкой условия, поэтому, если начальное условие ложно, то "оператор" не выполняется ни разу. Для включения в тело цикла нескольких операторов применяется составной оператор: Begin "операторы" end.

Цикл Repeat повторяется, если условие ложно (False), и заканчивается, если условие верно (True), т. е. цикл Repeat повторяется до выполнения условия.

Цикл Repeat заканчивается проверкой условия, поэтому "операторы" выполняются не менее одного раза. В теле цикла может записываться более одного оператора.

Циклы с условием обычно используются в тех случаях, если количество повторений блока операторов заранее не известно, например, при расчете суммы членов бесконечного ряда с заданной погрешностью.

Сумма членов бесконечной последовательности

a₁, a₂, a₃,..., a_n,...

называется бесконечным рядом и записывается в виде:

a₁ + a₂ + a₃ +... + a_n+...

Здесь a_n - общий член ряда.

Сумма конечного числа членов ряда называется частичной суммой и обозначается "S_n".

Если сумма членов бесконечного ряда имеет конечный предел "S", то ряд называется сходящимся. Для некоторых рядов получены формулы расчета суммы членов ряда. Например, сумма членов числового ряда:

1 + 1/32 + 1/52 +... + 1/(2*N-1)<sup2< sup=""> +...</sup2<>

имеет предел S = Pi²/8 и общий член a_n = images/(2*N-1)², где N = 1, 2, 3,...

Для сходящегося ряда вычисляется последовательность частичных сумм с заданной погрешностью. Абсолютная погрешность расчетов определяется по формуле Eps=abs(S-S_n), либо Eps=abs(a_n), если значение S неизвестно. Относительная погрешность расчетов определяется по формуле Eps_o=abs((S-S_n)/S), либо Eps_o=abs(a_n/S_n).

Частичные суммы вычисляются по формуле: S_n = S_n-1 + a_n

Для знакопеременного ряда следует добавить k1=-1, а в цикле: k1:=-k1, a_n=k1*a_n. В некоторых случаях "N"-ый член ряда выражается через "N-1"-ый, например, для ряда:

1 + 1/2! + 1/4! + 1/6! +... + 1/(2*N)! +...; N = 0, 1, 2,...

общий член ряда вычисляется по формуле: a_n = a_n-1*k;

Параметр k = a_n/a_n-1 - коэффициент роста вычисляется предварительно (до написания программы).

Для данного ряда

a_n = 1/(2*N)! = 1/(1*2*...*(2*N-2)*(2*N-1)*2*N)
a_n-1 = 1/(2*(N-1))! = 1/((2*N-2))! = 1/(1*2*...*(2*N-2))
k = a_n/a_n-1 = 1/((2*N-1)*2*N)

Здесь N! = 1*2*3*...*N; - вычисление факториала числа "N", причем 0! = 1.

Расчет частичных сумм производится в цикле с условием, например, для данного ряда операторами:

N:= 0; a:= 1; SN:= 1; S:= (e+1)/e; e:= 2.7182828; Repeat N:= N+1; k:= 1/((2*N-1)*2*N); a:= a*k; SN:= SN+a; Writeln('Частичная сумма Sn= ', Sn:11:6); Until abs(S-Sn) < eps; { eps - допустимая погрешность расчетов} Writeln('Сумма ряда S = ', SN:11:6);