
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение частоты и фазы колебанийСодержание книги Поиск на нашем сайте
Цель работы: научиться определять частоту колебаний методом прямого исследования сигнала, методом биений, методом фигур Лиссажу; научиться измерять разность фаз колебаний на входе и выходе RC-цепочки методом наложения сигналов и методом эллипса.
Оборудование: генератор электрических колебаний звуковой частоты ГЗЧМ, осциллограф MOS-620, модуль МО3 лабораторного комплекса ЛКЭ-6
Введение Известно, что в самом общем случае уравнение колебательного контура имеет вид:
Этот закон занимает особое положение благодаря свойствам самого колебательного контура сохранять гармонический вид колебаний при действии внешней гармонической э. д. с. В данном случае уравнение колебательного контура записывается как
или
Решение этого уравнения, как известно из математики, представляет собой сумму общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения. Нас будут интересовать только установившиеся колебания, т. е. частное решение этого уравнения (общее решение однородного уравнения экспоненциально затухает, и по прошествии некоторого времени оно практически исчезает, обращается в нуль). Это решение имеет вид q = qm cos ( ω t- ψ ), (4) где qm — амплитуда заряда на конденсаторе; ψ — разность фаз между колебаниями заряда и внешней э. д. с. ξ (1). Как мы увидим, qm и ψ определяются только свойствами самого контура и вынуждающей э. д. с. ξ, причем оказывается, что ψ > > 0, поэтому q всегда отстает по фазе от ξ. Чтобы определить постоянные qm и ψ, надо подставить (4) в исходное уравнение (3) и преобразовать полученное выражение. Мы же поступим несколько иначе (в целях достижения большей простоты): сначала найдем ток I и затем его выражение подставим в исходное уравнение (2). Попутно будет решен и вопрос с постоянными qm и ψ. Продифференцировав (4) по t, найдем: Запишем это выражение так: I=Im cos(ωt - φ ),(5) где Im – амплитуда тока; φ – сдвиг по фазе между током и внешней э. д. с. ξ, Im = ω qm,φ = ψ – π/2(6) Наша задача найти Im и φ. С этой целью мы поступим следующим образом. Представим иходное уравнение (2) в виде
где слева записана сумма напряжений на индуктивности L, сопротивлении R и емкости C. Таким образом, мы видим, что сумма этих напряжений равна в каждый момент внешней э.д.с. ξ. Учитывая соотношения (6), запишем:
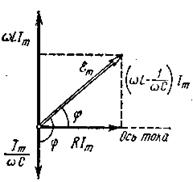
Из последних трех формул видно, что UR находится в фазе с током I, Uc отстает по фазе от на π/2, a UL опережает I на π/2. Все это можно наглядно представить с помощью векторной диаграммы, изобразив амплитуды напряжений URm = RIm, UCm = Im/ ω C, ULm = ω LIm и их векторную сумму, равную согласно (7) вектору величины ξm (рис. 1). Из прямоугольного треугольника этой диаграммы легко получить следующее выражение для Im и φ:
В соответствии с (6) и с формулами приведения
Рисунок 1. Векторная диаграмма напряжений
Векторная диаграмма оказывается весьма полезной при решении многих конкретных вопросов. Она позволяет наглядно, легко и быстро анализировать различные ситуации. Получим уравнение траектории, которую вычертит на экране осциллографа электронный луч при сложении перпендикулярных колебаний одинаковой частоты. Начало отсчета времени всегда можно выбрать так, чтобы начальная фаза первого колебания была равна 0. Тогда уравнения колебаний запишутся следующим образом:
где ψ – разность начальных фаз обоих колебаний. Выражения (14) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (14) время. Из первого уравнения (14) следует, что
поэтому
Представим далее косинус во втором уравнении (14) по формуле для косинуса суммы, подставляя при этом вместо cos ω0t и sin ω0t их значения из соотношений (15) и (16). В результате получим:
Уравнение (17) – это уравнение эллипса, оси которого повернуты относительно координатных осей OX и OY. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз ψ. При этом при x = 0
Порядок выполнения работы 1. Выполните п. 1 лабораторной работы № 2. 2. Включите осциллограф, а также кнопку питания модуля МО3 (она находится на задней стенке комплекса, имеет зеленый цвет). На экране осциллографа должны появиться синусоидальные колебания, порожденные LC-генератором. С помощью ручки регулировки сопротивления резистора R2 установите амплитуду синусоидального сигнала, поступающего на вход CH2 осциллографа, равной 2 В. 3. Измерьте по шкале осциллографа период колебания и определите его частоту. Оцените погрешность измерения. 4. С помощью второго коаксиального кабеля подайте на вход CH1 осциллографа синусоидальный сигнал произвольной частоты и амплитудой 2 В с генератора ГЗЧМ. Получите сумму колебаний, установив в зоне VERTICAL переключатель MODE в положение ADD. 5. Подбирая частоту сигнала ГЗЧМ, получите на экране биения с минимальной частотой. При этом частота ГЗЧМ практически дает частоту сигнала с LC-генератора. Запишите последнюю. Чем определяется погрешность измерений в данном случае? 6. Чтобы суммировать перпендикулярные колебания с наших генераторов, переведите в зоне HORIZONTAL ручку TIME/DIV в положение XY. Подбирая частоту сигнала ГЗЧМ, получите фигуры Лиссажу для соотношений частот 1:1, 1:2, 1:3, пользуясь рис. 7 в описании к лабораторной работе № 2. Рассчитайте, исходя из вида фигуры, для каждого соотношения частоту сигнала с LC-генератора. 7. Разберите LC-генератор и соберите RC-цепочку вида, показанного на рис. 2. Сигнал с ГЗЧМ частотой ν = 300 Гц подайте на вход RC-цепочки (контакты 35 и 57) и на вход СН1 осциллографа (коаксиальный кабель от входа СН1 подсоедините к тем же контактам – 35 и 57). Выходной сигнал с контактов 51 и 55 подайте на вход CH2 оциллографа. 8. Настройте осциллограф на двухканальный режим. Для этого в зоне VERTICAL установите переключатель MODE в положение DUAL. Используя в зоне TRIGGER регулятор LEVEL, получите устойчивое изображение двух сигналов.
Рисунок 2. RC-цепочка
9. Теория предсказывает, что частоты сигналов равны. Для измерения разности их фаз необходимо совместить средние значения («нулевые» линии), как показано на рис. 3.
Рисунок 3. Визуальная оценка разности фаз 10. Измерьте по шкале осциллографа период T и время запаздывания t. Учитывая, что фаза и время пропорциональны, определите разность фаз по формуле: 11. Для RC-цепочки (L = 0), согласно формуле (13), tg ψ = ω RC. Учитывая, что сопротивление R = R14 = 3 кОм, электроемкость С = С7 = 0,1 мкФ, рассчитайте ψ по этому соотношению и сравните с подсчитанным в п. 10. 12. Переведите в зоне HORIZONTAL ручку TIME/DIV в положение XY. Теперь на экране наблюдается результат суммы перпендикулярных колебаний с одинаковой частотой – эллипс (рис. 4).
Рисунок 4. Сумма колебаний одинаковой частоты 13. Согласно соотношению (18) и в соответствии с рис. 4, при x = 0 14. Разберите схему, выключите питание, уберите оборудование. 15. Подготовьте отчет по работе.
Контрольные вопросы
Литература
Лабораторная работа № 4
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.01 с.) |

 , где L и С – индуктивность и емкость контура, R – его сопротивление. Рассмотрим случай, когда в контур включена внешняя переменная э. д. с. ξ, зависящая от времени по гармоническому закону:
, где L и С – индуктивность и емкость контура, R – его сопротивление. Рассмотрим случай, когда в контур включена внешняя переменная э. д. с. ξ, зависящая от времени по гармоническому закону: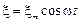 . (1)
. (1) (2)
(2)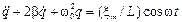 . (3)
. (3) .
. , (7)
, (7)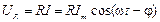 (8)
(8) (9)
(9) (10)
(10) , (11)
, (11) .
.  (12)
(12) .
. 
 и
и  , (14)
, (14) , (15)
, (15) . (16)
. (16) . (17)
. (17) . (18)
. (18)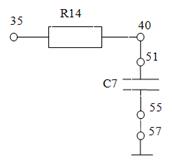

 .
.
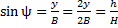 . Рассчитайте ψ. Усредните оба экспериментальных результата и оцените погрешность.
. Рассчитайте ψ. Усредните оба экспериментальных результата и оцените погрешность.


