
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что понимается под доверительным интервалом.Содержание книги
Поиск на нашем сайте
А) нижняя граница – обобщающая характеристика выборочной совокупности минус предельная ошибка Б) верхняя граница – обобщающая характеристика плюс предельная ошибка.
46. Смысл и значение коэффициента вариации, примеры
Коэффициент вариации является относительным показателем и применяется для сравнения вариации разных признаков. В нем именованный показатель вариации (среднее линейное или среднеквадратическое отклонение) соотносится со средней арифметической или заменяющей ее величиной (например модой).но обычно это Vσ = σ/x или чаще Vσ = σ/x *100 Исчисленный по среднему линейному отклонению показатель называют линейным коэффициент вариации. В количественном отношении V коэффициент представляет собой своеобразную долю среднего отклонения в средней арифметической величине выражается в процентах. Его универсальность заключается в том, что устраняет несопоставимость различных единиц измерения признака и различных величин средних арифметических. Коэффициент вариации является критерием однородности совокупности; если < 33-35%, то совокупность однородна по данному признаку.
49. Возможно ли одновременно уменьшить ошибку 1 и 2 рода
ά- ошибка первого рода – вероятность отклонить верную гипотезу(от 0,01 до 0,1). Доверительная вероятность= 1-ά Β - Ошибка второго рода – вероятность принять неверную гипотезу. Одновременно нельзя уменьшить ошибки 1 и 2 рода. Что следует понимать под ошибкой выборки. Какую роль играет коэффициент доверия.
Ошибка выборки — это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.
При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:
Предельная ошибка выборки При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки. Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:
Предельная ошибка выборки при повторном отборе определяется по формуле:
Средние индексы
1. Индексы как средние величины: 1.1Индекс физического объема 1.2Индекс цен Пааше
, где - индекс (темп прироста), характеризующий изменение цены на каждый отдельный товар (индивидуальный индекс).
Индексы сезонности. Построение сезонной волны 1) Метод простых средних: а) определяется средняя хронологическая для каждого месяца 2) Метод сравнения фактического и сглаженного уровней а) метод скользящего среднего уровня: б) метод аналитического выравнивания: Колеблемость уровня ряда измеряется средним отклонением индекса сезонности i сез от 100%:
50. Цепные индексы получают сопоставлением текущих уровней с предшествующим. Базисные получают сопоставлением с уровнем периода принятого за базу сравнения. 51. Графический образ- геометрические знаки, совокупность точек, линии, фигуры, с помощью которых изобр. стат. величины. Для размещения геометрических знаков нужна система координат, самая распространенная – прямоугольная система, выбрать масштаб. СТАТИСТИЧЕСКИЕ ГРАФИКИ График – чертеж, на котором при помощи условных геометр. фигур изображаются стат. данные. В результате этого достигается наглядная хар-ка изучаемой стат. совокупности. Правильно построенный график делает стат. информацию более выразительной, запоминающейся и удобно воспринимаемой. Графики в статистике имеют не только иллюстративное значение, они позволяют получить доп. знания о предмете исследования, к-рые в цифровом варианте остаются скрытыми. Любое стат. исследование на основе какого-либо метода в конечном итоге дополняется использованием графического метода.
Знак Варзара. Варзар предложил использовать прямоугольные фигуры для графического изображения трех показателей, один из которых является произведением двух других. В каждом таком прямоугольнике основание пропорционально одному из показателей — сомножителей, а высота его соответствует второму показателю. Площадь прямоугольника равна величине третьего показателя, являющегося произведением двух первых. Располагая рядом несколько прямоугольников, относящихся к разным показателям, можно сравнивать не только размеры показателя — произведения, но и значения показателей — сомножителей. ОСНОВНЫЕ ПРАВИЛА В общем расположении на поле графических образов они размещаются слева направо. При этом масштабные ориентиры графика по горизонтальной шкале, как правило, размещаются от его нижней части. Для вертикальной шкалы масштабные ориентиры обычно размещаются в левой части графика. В график по возможности следует включать исходные данные. Если это нецелесообразно, то исходные данные должны в табличной форме сопровождать график. Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко можно было отсчитать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс. Общим требованием графического метода является то, что факторные признаки размещаются на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки — по вертикальной шкале и читаются снизу вверх. При этом важно, чтобы заголовок графика был бы кратким, но достаточно четко пояснял основное его содержание.
52. (51+52)Графики бывают: диаграммы, статистические карты, столбиковые, полосовые, круговые, секторные, линейные, полигон- изображение дискретных рядов, гистограмма-изображение интервальных рядов, кумулята – то же самое, картограммы 53. Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Для результативного при-ка необходимо опр величину интервала. Факторный признак x-в строках, а результативный y-в столбцах. Нужно установить расположение основной части частот. Уже можно делать выводы о существовании или отсутствии корр. связи.
57. Хи2 - критерий согласия Пирсона. - специальные статистические показатели, которые оценивают согласованность эмпирических и теоретических частот. Критерии согласия дают общую оценку степени близости эмпирического распределения и теоретического, однако не содержат информации о характере расхождения между ними(для этого используются специальные показатели – коэффициент асимметрии и эксцесс) К критериям согласия относятся критерии Пирсона, Ястремского, Романовского, Колмогорова Пирсона χ2 = Σ ((nэ-nт)2)/ nт), где nэ, nт эмпирические и теоретические частоты С помощью χ2 по специальным таблицам определяется вероятность.
d) χ2 > χтабл. Расхождение между m и m’ нельзя признать случайным => теоретический закон подобран плохо.
e) …< … Расхождение между m и m’ НОСИТ ЧИСТО СЛУЧАЙНЫЙ ХАРАКТЕР, ЗАКОН ПОДОБРАН УДАЧНО f) …=… критерий не может определить случайный или не случайный характер.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.223.120 (0.011 с.) |


 связана со средней ошибкой выборки
связана со средней ошибкой выборки  отношением:
отношением: 





 Индекс цен Ласпейреса:
Индекс цен Ласпейреса: 
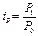
 Форма индекса среднего из индивидуальных адаптирована к практике статистического измерения цен, основанной на выборочных наблюдениях. Выборочные статистические обследования позволяют, во-первых, выяснить, как менялись цены на основные товары и товарные группы. Во-вторых, установить долю каждой товарной группы в общем объеме товаров. Чтобы оценить динамику цен по таким данным формулу Ласпейреса представляют в виде индекса среднего из индивидуальных.
Форма индекса среднего из индивидуальных адаптирована к практике статистического измерения цен, основанной на выборочных наблюдениях. Выборочные статистические обследования позволяют, во-первых, выяснить, как менялись цены на основные товары и товарные группы. Во-вторых, установить долю каждой товарной группы в общем объеме товаров. Чтобы оценить динамику цен по таким данным формулу Ласпейреса представляют в виде индекса среднего из индивидуальных.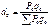 d0 – удельный вес стоимости каждого товара в общем стоимостном объеме всех товаров в базисном периоде.
d0 – удельный вес стоимости каждого товара в общем стоимостном объеме всех товаров в базисном периоде.
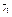 б) средняя хронологическая общая:
б) средняя хронологическая общая:  Индекс сезонности:
Индекс сезонности: 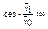

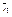


 Среднее квадратичное отклонение
Среднее квадратичное отклонение 




