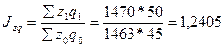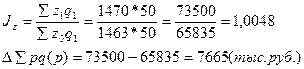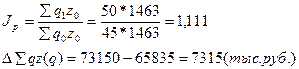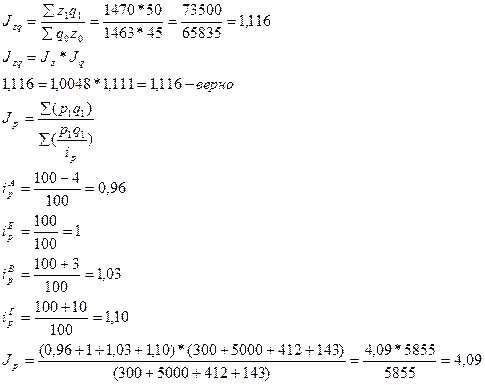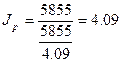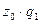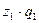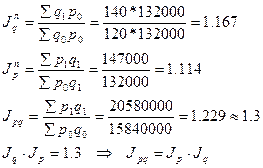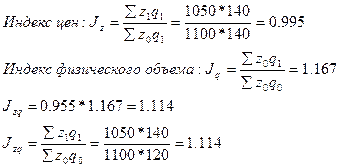Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстраполяция и интерполяция в динамических рядахСодержание книги
Поиск на нашем сайте Расчет индекса сезонности Экстраполяция и интерполяция в динамических рядах Понятие о статистических рядах динамики
Динамика –это изменение общего процесса или явления во времени. Ряды динамики – это ряды последовательно расположенных в хронологическом порядке показателей, характеризующих динамику общего явления или процесса. Динамические ряды характеризуются двумя показателями: t – показатель времени, момент времени или период; y – статистические показатели, если уровень ряда характеризует явления.
Классификация рядов динамики:
- ряд абсолютных величин - ряд относительных величин - ряд средних величин
Рядом динамики относительных величин называется такой ряд, уровень которого характеризует изменения относительных размеров изученных явлений во времени. Рядом динамики средних величин называется такой ряд, уровни которого характеризуют изменение средних размеров изученных явлений во времени.
- моментный – уровни ряда даны на определенные моменты времени - интервальные – уровни ряда за определенные интервалы времени
Интервал моментного ряда – это период между датами, на которые приводятся данные; величина его зависит от характера явлений – быстро развивающиеся явления должны иметь более короткий интервал. В моментном ряду в каждом последующем уровне содержится полностью или частично предыдущий уровень, поэтому суммировать уровни моментного ряда нельзя, так как это приводит к повторному счету, их можно только вычитать. Интервал в интервальном ряду – это промежуток времени, за которым обобщены приводимые сведения, это накопленный итог учёта результатов деятельности, их можно складывать, так как они будут характеризовать развивающиеся явления за более длительный срок.
- равноотстоящие уровню - неравноотстоящие уровню
- изолированный ряд – ведется анализ во времени одного показателя - комплексный ряд – дана динамика нескольких показателей, характеризующих одно явление
Сопоставимость в рядах динамики Чтобы построить ряд динамики, необходимо обеспечить сопоставимость его показателей. Причины несопоставимости показателей ряда динамики:
Основные вопросы в ликвидационной несопоставимости в рядах динамики: 1. Пересчитываются старые данные в новых территориально – административных границах 2. Выбираются равные и одноименные интервалы 3. Смыкаются показатели рядов динамики путём замены абсолютных уровней относительными 4. Данные пересчитываются в одних единицах измерения и по одной методике расчета
Смыкание динамических рядов – основной прием приведения их к сопоставимому виду
Смыкание рядов – объединение двух или более рядов, характеризующих явление в один. ПРИМЕР. Имеются данные, характеризующие размер товарной продукции группы предприятий одной из областей.
Первый приём смыкания: Определяется для 2003 года коэффициентом соотношения уровней двух рядов: 22,8:21,2 = 1,1 Умножая на этот коэффициент уровни первого ряда получим их сопоставимость с уровнем второго ряда.
Второй приём: уровни ряда, в котором произошли изменения (2003) как до изменений, так и после изменений (21,2 и 22,8) принимаются за 100%, а остальные пересчитываются в процентном соотношении к этим уровням соответственно.
Выявление основных тенденций ряда динамики – основные приемы обработки рядов динамики
А) Укрупнение интервала Содержание этого приема заключается в том, что первоначальный ряд преобразуется и заменяется другим, показатели которого обхватывают большие периоды времени. ПРИМЕР: Преобразование месячных данных в квартальные.
На основании по месячным данным о добыче нефти составим новый ряд квартальных данных.
Б) Метод скользящей средней Расчет скользящей средней производится в последующем порядке:
ПРИМЕР: Производительность труда на магистральном транспорте газа.
При помощи скользящей средней получен новый ряд, показатели которого более четко характеризуют тенденцию развития. В результате такого выравнивания сглаживаются незначительные случайные колебания и более отчетливо проявляются общие направления развития.
В) Метод аналитической выравнивающей Аналитическое выравнивание ряда динамики может производиться по различным видам уравнений: - Прямой - Парабола - Гипербола и др.
Математический критерий правильности определения общей тенденции развития уровней ряда динамики основан на нулевом и минимальном свойствах средней арифметической. Чем правильнее определена общая тенденция развития, тем меньше будет сумма квадратов отклонений эмпирических данных уровней ряда динамики от выровненных (теоретических), а при правильном определении общей тенденции эта величина будет минимальной.
Расчет индекса сезонности
Для изучения рядов, характеризующих поквартальную или помесячную динамику явления большое значение приобретают сезонные колебания – это такие изменения уровня ряда, которые вызываются влиянием времени года. Сезонные колебания необходимо изучать для точного планирования, учета и определения мероприятий, необходимых для уменьшения или увеличения сезонных колебаний. Сезонные колебания характеризуются специальными показателями, которые называются индексами сезонности, а совокупность этих индексов образуют сезонную волну. Индекс сезонности ( Для выявления сезонности рассматриваются данные по месяцам за несколько лет (обычно за 3 года).
Анализ сезонности на основании метода простой средней: Применяется для анализа сезонности явлений, уровни которой не имеют резко выраженных тенденций увеличения или уменьшения. Сущность этого метода заключается в определении сезонной волны как процентного отношения средних квадратичных уровней к их общей средней. ПРИМЕР: Анализ сезонности объемов добычи нефти по организации методом простой средней.
Из таблицы видно, что в январе меньше добывающей нефти, в среднем за 3 года в январе добтывалось на 9,4% меньше среднесписочной добычи, а в декабре на 7% больше от среднемесячной. Применение метода простой средней для расчета сезонной волны дает возможность нейтрализовать случайные колебания показателей исследуемого ряда динамики и определить сезонные колебания в среднем за весь период.
ПРАКТИКА. Задача 1. Построить интервальный ряд распределения; найти средний возраст, структурные средние, относительный показатель вариации. Дать графическое изображение в виде гистограммы и полигона частот.
1) h = R/k = (Xmax – Xmin)*k h = (38 – 18)/5 = 4
2)
3)
4)
5) Полигон частот
6) Гистограмма
Задача 2. Определить на каком участке состав рабочих по стажу работы более однороден.
1)
Задача 3. Имеются данные об объёме пассажирооборота.
Вычислить и проставить в таблицу уровни ряда динамики и недостающие показатели динамики. 1)
2)
3)
4)
Задача 4.
1) 2)
3) 358,5 - 345,7 = 12,8
4)
1997:
Абсолютный прирост: 1995: 358,49 – 345,7 = 12,79 Коэффициент роста: 1994: Темп прироста:
Задача 5. Определить абсолютное и относительное изменение среднегодовой стоимости имущества в 1997 году по сравнению с 1995 и 1996 годами.
Абсолютный прирост: 95: 87,375 – 87 = 20,375 96: 87,375 – 74,25 = 13,125
Относительный прирост:
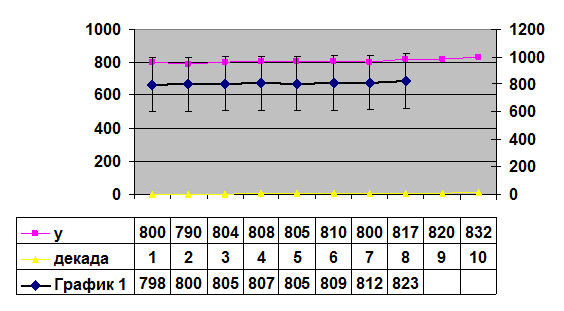
Задача 6. На 1 октября в списке предприятия А числились 25 человек; с 10 октября были приняты на работу 6 человек, а с 12 октября уволены 4 человека; с 25 октября приняты 6 человек. На предприятии В на 1 октября числились 32 человека; с 15 октября были приняты 5 человек; а с 28 октября уволены 6 человек. Определить на каком предприятии и на сколько среднесписочная численность была больше (в абсолютном выражении и в процентах). Изобразить динамику численности работников предприятия с помощью линейной диаграммы. y = 25 человек, t = 9 дней.
2)
На первом участке состав рабочих по стажу был однороден и составил 17,5%.
Задача 7. Имеются данные о добыче угля за первую декаду.
Произвести сглаживание ряда методом трехчленной скользящей средней, дать первичного и сглаживания рядов.
Задача 8. Численность населения региона возросла за период с 1.01.95 – 1.01.98 на 4,2%. При этом удельный вес мужского населения за этот период увеличилась с 42,1% до 44,3%. Определить показатели динамики численности мужского и женского населения региона.
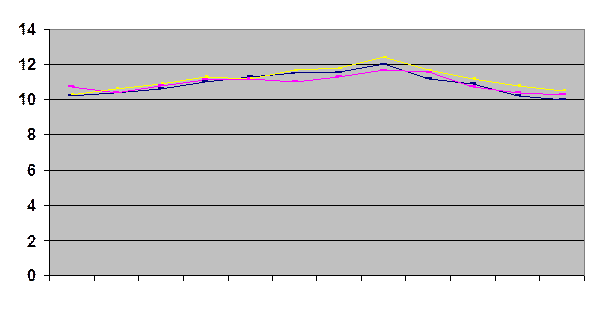
Задача 9. Имеются данные об объеме перевозок.
Требуется: 1) Выявить наличие сезонной неравномерности (графический метод); 2) Определить величину сезонной волны, используя индексы сезонности.
Максимальные и минимальные объемы перевозок практически приходятся на одни и те же месяцы, поэтому применяется следующая формула:
Формула средней арифметической взвешенной:
По месяцам:
СТАТИСТИКА ПРОМЫШЛЕННОСТИ Тема: Статистика продукции
ПРАКТИКА Задача 1. Определить индексы товарооборота, физического объема и цены, показать их взаимосвязь в относительно – стоимостном выражении.
1) Товарооборот снизился на 10,2 %.
2)
3)
Задача 2. Определить, на сколько процентов увеличится выпуск продукции по предприятию.
Задача 3. Определить абсолютное изменение общей суммы затрат за счет изменения выпуска продукции и её себестоимости.
Себестоимость:
- за февраль: 73 500 – 65 835 = 7 665 руб.
Задача 4. В отчетном году было реализовано: Товара А на 300 млн. руб.; Товара Б на 5 млрд. руб.; Товара В на 412 млн. руб.; Товара Г на 143 млн. руб. Исчислить общий индекс цен на все товары, если цены на товар А – увеличили на 4,2%, товар Б без изменений, В, Г – на 3% и 10% соответственно.
1) Общий индекс цен:
2) Индекс физического объёма:
3) Индекс товарооборота:
Общий индекс цен в агрегатной форме:
Задача 5.
Определить относительные и абсолютные изменения общей суммы затрат всего и в том числе за счет: А) изменения выпуска продукции; Б) изменения ее себестоимости.
А) Относительные и абсолютные изменения за счет выпуска продукции
Б) Изменение себестоимости
Расчет индекса сезонности Экстраполяция и интерполяция в динамических рядах
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

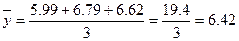
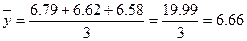
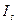 )– это среднее вычисленное из процентных отношений по одноименным месяцам фактических уровней к уровням выровненным.
)– это среднее вычисленное из процентных отношений по одноименным месяцам фактических уровней к уровням выровненным.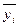
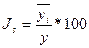
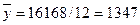 (тыс. т.)
(тыс. т.)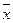
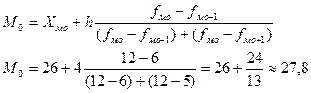
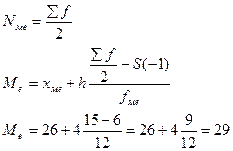
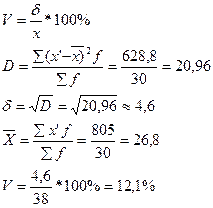


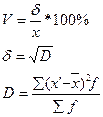
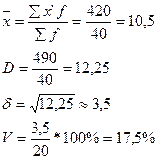
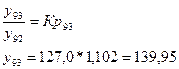
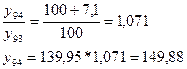
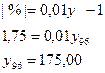
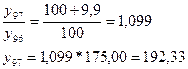
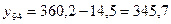

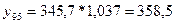
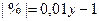
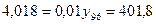
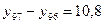
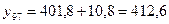
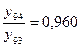
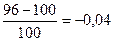
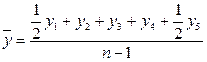
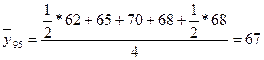 млн. руб.
млн. руб.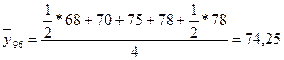 млн. руб.
млн. руб.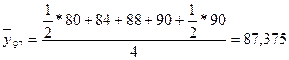 млн. руб.
млн. руб. ; стоимость увеличилась на 3,04%
; стоимость увеличилась на 3,04%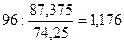 ; стоимость увеличилась на 17,6%
; стоимость увеличилась на 17,6%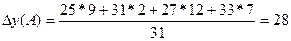 чел.
чел. чел.
чел.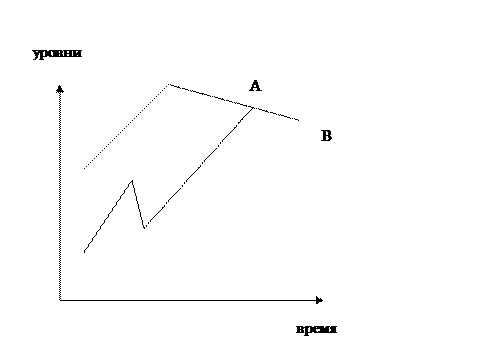
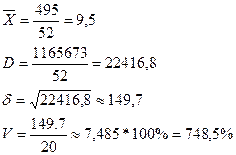
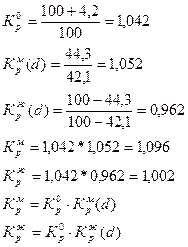

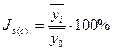
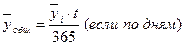


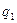
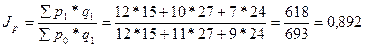
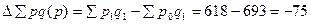 тыс. руб.
тыс. руб.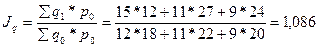
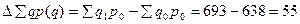 тыс. руб.
тыс. руб.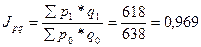
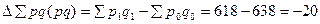 тыс. руб.
тыс. руб.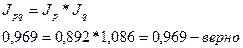
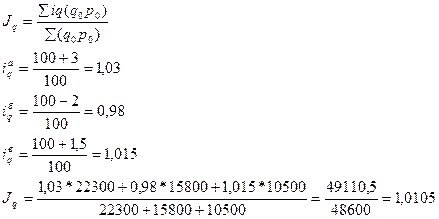
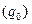
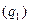
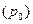
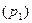
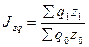
 - за январь:
- за январь: 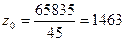 руб.
руб. руб.
руб.