
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация и назначение группировокСодержание книги
Поиск на нашем сайте
Классификация и назначение группировок 1. Типологическая группировка. Решает задачу выявления и характеристики социально-экономических типов. Для типологической группировки не являются произвольным ни выбор группировочного признака, ни установление числа интервалов и их границ. Выделение групп (типов) производится на основании одного или нескольких существенных признаков, в результате тщательного теоретического и логического анализа. 2. Структурная группировка. Позволяет описать соотношение между выделенными группами в едином целом и проследить структурные сдвиги, происходящие в изучаемой совокупности во времени. При построении структурной группировки обязателен показатель численности групп, представленный частотой (количество объектов в группе) либо удельным весом каждой группы. 3. Аналитическая группировка. Решает задачу установления связи, зависимости между двумя статистическими признаками. При построении аналитической группировки всегда выделяются два признака объектов статистической совокупности – факторный и результативный. Факторный признак – это признак, оказывающий влияние на другие статистические признаки изучаемых объектов наблюдения. Результативный признак – признак, который зависит от факторного.
3. Аналитическая группировка – назначение, примеры построения. Простейшие примеры факторных и результативных признаков представлены в таблице 3. Таблица 3 Факторные и результативные признаки
4. Классификация, назначение статистических таблиц. Особенности построения. Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица позволяет охватить материалы статистической сводки в целом, она также является системой мыслей об исследуемом объекте, излагаемых цифрами на основе определенного порядка в расположении систематизированной информации. По внешнему виду статистическая таблица представляет собой ряд пересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали – графы (столбцы, колонки), которые в совокупности составляют как бы скелет таблицы. В образовавшиеся внутри таблицы клетки записывается информация. Составленную таблицу принято называть макетом таблицы, в котором мысленно определяются в деталях цель обследования, объем разработки материалов сводки. Статистическая таблица имеет свое подлежащее и сказуемое. Подлежащее таблицы показывает, о каком явлении идет речь в таблице, и представляет собой группы и подгруппы, которые характеризуются рядом показателей. Сказуемым таблицы называются числовые показатели, с помощью которых характеризуется объект, т. е. подлежащее таблицы. Показатели, образующие подлежащее, располагают в левой части таблицы, а показатели, составляющие сказуемое, помещают справа. Составленная и оформленная статистическая таблица должна иметь общий, боковые и верхние заголовки. Общий заголовок обычно располагается над таблицей и выражает ее основное содержание. Помещенные слева боковые заголовки раскрывают содержание строк подлежащего, а верхние – вертикальных граф (сказуемого таблицы), В зависимости от построения подлежащего делятся на три вида: перечневые, групповые и комбинационные. Таблицы, в подлежащем которых приводится перечень территорий (районов, областей и т. п.), называются перечневыми территориальными. Групповые статистические таблицы дают более информативный материал для анализа изучаемых явлений благодаря образованным в их подлежащем группам по существенному признаку или выявлению связи между рядом показателей. Комбинационными называют статистические таблицы, которые имеют в подлежащем группировку по двум или более группи–ровочным признакам, связанным между собой. 5. Классификация статистических графиков. Назначение, примеры составления. Статистический график – чертеж, на котором при помощи условных геометрических фигур (линий, точек или других символических знаков) изображаются статистические данные. Статистический график – это наглядная характеристика изучаемой статистической совокупности. Правильно построенный график делает статистическую информацию более выразительной. Графический метод находит широкое применение в коммерческой деятельности. Он служит иллюстрацией сложившегося положения дел на рынке товаров и услуг, конъюнктуры спроса и предложения, рекламы товаров. Статистические графики имеют важное аналитическое значение. По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы. Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. Картограмма – это схематическая (контурная) географическая карта или план местности, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (штриховки, расцветки, точек). Картограммы подразделяются на фоновые и точечные. Вторая большая группа статистических карт – это картодиаграмма, которая представляет собой сочетание контурной карты (плана) местности с диаграммой. Используемые геометрические символы (столбики, круги и др.) на картодиаграмме размещают по всей карте. Преимущество картодиаграммы в том, что она не только дает представление о величине изучаемого показателя на различных территориях, но и изображает пространственное размещение изучаемого показателя.
Пример прострой средней арифметической величины. Данные о заработной плате рабочих – сдельщиков представлены в таблице 4. Таблица 4
По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта х1 встречается в совокупности 2 раза, варианта х3 - 16 раз и т. д. Число одинаковых значений признака в рядах распределения называется частотой, или весом, и обозначается символом n. Вычислим среднюю заработную плату одного рабочего
Средняя зависит не только от значений признака, но и от их частот, от состава совокупности, от ее структуры.
Средняя гармоническая. Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов и частот, т. е. значения х и f. Формула для расчета средней гармонической простой имеет вид
Пример. Издержки производства и себестоимость единицы продукции по трем цехам предприятия характеризуется данными таблицы 6. Таблица 6
Определим среднюю себестоимость изделия. Главным условием выбора формы средней величины является экономическое содержание показателя и исходные данные. В данном случае
Получаем результат
Соответственно, средняя гармоническая тождественна средней арифметической. Средняя геометрическая Если имеется n коэффициентов роста, то формула среднего коэффициента:
Это формула средней геометрической. Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего. Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д. Средняя хронологическая величина применяется для определения среднего уровня в моментных рядах динамики. Существует два вида рядов динамики: моментные; интервальные. Интервальные – это такие ряды в которых данные приводятся за определенный период времени (месяц, год). Средний уровень ряда в интервальном ряду определяется по средней арифметической простой. Моментные – это такие ряды, где данные представлены на определенный момент времени (на определенную дату). Если интервалы времени между датами равны, то расчет средней ведут по формуле средней хронологической простой:
Если интервалы между датами в моментных рядах не одинаковые, то расчет ведется в два этапа: по средней хронологической взвешенной: определяется средняя внутри каждого интервала времени по среднеарифметической простой; определяется общая средняя по среднеарифметической взвешенной, где частотами являются интервалы между датами.
10. Способы оценки вариации статистических признаков, интерпретация показателей вариации. Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую. Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако значения признака могут значительно отличаться друг от друга по степени вариации, и в этом случае средняя будет недостаточно показательной характеристикой совокупности. Например, заработная плата рабочих 408, 1200, 2600 рублей. Средняя заработная плата равна 1403 рубля и нетипична для данной совокупности, плохо отражает ее. Поэтому нужны измерители, отражающие степень близости отдельных единиц к средней. К таким показателям относится размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Размах вариации – разность между наибольшим (Хmaх) и наименьшим (Хmin) значениями признаков:R= Хmaх-Xmin. Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит только от величины крайних значений признака, поэтому область его применения ограничена однородными совокупностями. На практике он находит применение в предупредительном контроле качества продукции.Точнее характеризует вариацию признака показатель, основанный на учете вариации всех значений признака. К таким показателям относятся дисперсия и среднее квадратичное отклонение. Дисперсия Дисперсия рассчитывается по следующим формулам: для несгруппированных данных для сгруппированных данных
Среднее квадратичное отклонение S представляет собой корень квадратный из дисперсии:для несгруппированных данных:
для сгруппированных
Дисперсия и среднее квадратическое отклонение – наиболее широко применяемые показатели вариации. Объясняется это тем, что дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака. При сравнении вариации различных признаков в одной и той же совокупности или же при сравнении вариации одного и того же признака в нескольких совокупностях с различной средней величиной пользуются коэффициентом вариации. Коэффициент вариации рассчитывается по формуле Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Таким образом, среднее квадратическое отклонение показывает, на сколько в среднем отличаются отдельные значения признака от среднего значения. Коэффициент вариации показывает, на сколько процентов в среднем отличаются отдельные значения признака от средней величины. Совокупность считается однородной, если коэффициент вариации не превышает 33 %. При коэффициенте вариации более 33% можно говорить о том, что изучаемая совокупность неоднородна, средняя не отражает адекватно изучаемую совокупность и для ее описания необходимо разбить совокупность на несколько более однородных групп.
Классификация и назначение группировок 1. Типологическая группировка. Решает задачу выявления и характеристики социально-экономических типов. Для типологической группировки не являются произвольным ни выбор группировочного признака, ни установление числа интервалов и их границ. Выделение групп (типов) производится на основании одного или нескольких существенных признаков, в результате тщательного теоретического и логического анализа. 2. Структурная группировка. Позволяет описать соотношение между выделенными группами в едином целом и проследить структурные сдвиги, происходящие в изучаемой совокупности во времени. При построении структурной группировки обязателен показатель численности групп, представленный частотой (количество объектов в группе) либо удельным весом каждой группы. 3. Аналитическая группировка. Решает задачу установления связи, зависимости между двумя статистическими признаками. При построении аналитической группировки всегда выделяются два признака объектов статистической совокупности – факторный и результативный. Факторный признак – это признак, оказывающий влияние на другие статистические признаки изучаемых объектов наблюдения. Результативный признак – признак, который зависит от факторного.
3. Аналитическая группировка – назначение, примеры построения. Простейшие примеры факторных и результативных признаков представлены в таблице 3. Таблица 3
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.170 (0.008 с.) |

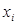 ), тыс. руб.
), тыс. руб.

 = 1,1
= 1,1
 = 2
= 2
 = 1,3
= 1,3
 = 6
= 6
 = 16,
= 16,
 = 16
= 16
 = 1,9
= 1,9
 = 12
= 12
 = 2,2
= 2,2
 = 14
= 14
 в тыс. руб.:
в тыс. руб.: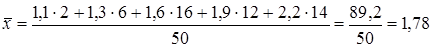 .
. .
. .
. тыс. руб.
тыс. руб.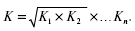
 (12)
(12) – это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. В зависимости от исходных данных дисперсия может быть невзвешенной (простой) или взвешенной.
– это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. В зависимости от исходных данных дисперсия может быть невзвешенной (простой) или взвешенной.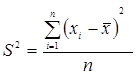 ,
, .
. ;
; .
. .
.


