
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи аналізу взаємозв'язківСодержание книги
Поиск на нашем сайте
6.1. З наведених пар ознак результативними є: а) розмір податку; б) розмір прибутку; в) сукупний доход сім'ї; г) заощадження. Відповіді: 1) а, г; 2) а, в; 3) б, в; 4) б, г. 6.2. З наведених пар ознак факторними є: а) сума виплачених дивідендів; б) розмір акціонерного капіталу; в) ціни на товар; г) попит на товар. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.3. Із зміною значень факторної ознаки стохастична залежність проявляється: а) у зміні індивідуальних значень результативної ознаки; б) у зміні розподілу сукупності за результативною ознакою. Кореляційна залежність проявляється: в) у змін і розподілу сукупності за факторною ознакою; г) у зміні середніх значень результативної ознаки. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б,г. 6.4. За наявності стохастичного зв'язку умовні розподіли сукупності за результативною ознакою: а) обов'язково різні; б) можуть бути однаковими. У випадку кореляційного зв'язку середні умовних розподілів: в) обов'язково різні; г) можуть бути однаковими. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.5. З наведених залежностей кореляційними є: а) плата за кредит від проценту за користування ним; б) молочна продуктивність корів від рівня їх годівлі. Відповіді: 1) а; 2) б; 3) а, б; 4) –. 6.6. З наведених залежностей кореляційними є: а) собівартість продукції від обсягу виробництва та виробничих витрат; б) урожайність сільськогосподарської культури від якості ґрунту. Відповіді: 1) а; 2) б; 3) а, б; 4) –. 6.7. Кореляційне відношення це: 2) частка між групової дисперсії у загальній; 6.8. Кореляційне відношення використовують для оцінки щільності зв'язку, якщо кількісними ознаками є: а) лише факторна ознака; б) лише результативна ознака; в) обидві ознаки кількісні; г) обидві ознаки описові. Відповіді: 1) а; 2) б; 3) б, в; 4) в, г. 6.9. Якщо n ^2=0, то це означає, що: а) розбіжності між груповими середніми відсутні; б) значення варіант в межах груп однакові; в) зв'язок відсутній; г) зв'язок функціональний. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.10. Якщо факторна та результативна ознаки є кількісними, то для аналізу зв'язку між ними застосовують: а) комбінаційний розподіл за двома ознаками; б) рівняння регресії; в) аналітичне групування. Відповіді: 1) б; 2) а, б; 3) б, в; 4) а, б, в. 6.11. Якщо факторна ознака описова, а результативна кількісна, то для аналізу зв'язку між ними застосовують: а) комбінаційний розподіл за двома ознаками; б) рівняння регресії; в) аналітичне групування. Відповіді: 1) в; 2) а, в; 3) а, б; 4) а, б, в. 6.12. Відповіді: 1) 0,56; 2) 0,68; 3) 0,76; 4) 0,32. Дані, заєрестровані районною службою зайнятості, свідчать про зв’язок між рівнем освіти безробітних та терміном перерви у роботі:
Загальна дисперсія терміну перерви у роботі становить 5.8. Оцінити щільність зв’язку за допомогою кореляційного відношення. Пояснити його зміст. Перевірити істотність зв’язку з ймовірністю 0.95. Розв’язок:
Кореляційне відношення показує, що 68% варіації середнього терміну переви у роботі пояснюється варіацією рівня освіти. Визначимо ступені вільності: k1 = m-1= 3-1 = 2 k2 = n-m = 200-3 = 197
6.13. Трудомісткість вирощування озимої пшениці залежить від ступеня механізації виробничих процесів: Ступінь Кількість Трудомісткість 1 ц пшениці, механізації підприємств люд-год. Високий 8 4,5 Середній 12 6,0 Низький 10 6,6 Вцілому З0 5,8 Загальна дисперсія трудомісткості вирощування пшениці становить 1,36. Визначте кореляційне відношення. Відповіді: 1) 0,68; 2) 2,00; 3) 0,50; 4) 0,058. 6.14. За результатами вибіркового обстеження виявлена залежність успішності студентів від якості викладання спецкурсу: Оцінка якості Кількість Середній бал викладання спецкурсу студентів, осіб успішності студентів Висока 10 4,5 Середня 25 4,1 Низька 15 3,5 Вцілому 50 4,0 Загальна дисперсія середнього балу успішності студентів дорівнює 0,2. Визначте кореляційне відношення. Відповіді: 1) 0,65; 2) 0,85; 3) 0,35; 4) 1,17. 6.15. Визначте кореляційне відношення для оцінки щільності зв'язку між концентрацією сірки в чавуні та процентом браку у виливках: Концентрація сірки в Середнійпроцент Кількість виливок чавуні, % бракуувиливках 0,1–0,2 60 5 0,2–0,3 100 9 0,3–0,4 40 20 Вцілому 200 10 Загальна дисперсія процента браку становить 50. Відповіді: 1) 0,59; 2) 0,84; 3) 0,56; 4) 0,41. 6.16. Якщо з n^2 (0,95) =0,33, то це свідчить проте, що: 1) у 95 випадках із 100 можна одержати значення з, яке перевищує0,33; 2) у 95 випадках із 100 можна одержати значення з, яке не перевищує 0,33; 3) кореляційне відношення в аналітичному групуванні дорівнює 0,33. 6.17. Аналітичне групування 66 комерційних банків характеризує зв'язок між розміром капіталу та рівнем його прибутковості. Загальна дисперсія прибутковості капіталу - 25, міжгрупова- 16, кількість груп- 6. Кореляційне відношення становить: а) 0,36; б) 0,64. За умови, що критичне значення 2 з 1-0,05 (5,60)=0,165, істотність зв'язку: в) доведена; г) недоведена. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. Розв’язок: між групова/загальну = 16/25 = 0,64 Кореляційне відношення показує, що 64% варіації розміру капіталу пояснюється варіацією рівня його прибутковості. Визначимо ступені вільності: k1 = m-1= 6-1 = 5 k2 = n-m = 66-6 = 60
6.18. Аналітичне групування 30 фермерських господарств характеризує залежність між м'ясною продуктивністю птиці та забезпеченістю фуражним зерном. Виділено 4 групи, середня з групових дисперсій становить -27, між групова дисперсія- 81. Кореляційне відношення дорівнює: а) 0,75; б) 0,33. За умови, що критичне значення 2 з 1-0,05 (3,26)=0,256, істотність зв'язку: в) доведена; г) недоведена. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. Розв’язок: Кореляційне відношення показує, що 75% варіації м’ясної продуктивності птиці пояснюється варіацією забезпеченості фуражним зерном. Визначимо ступені вільності: k1 = m-1= 4-1 = 3 k2 = n-m = 30-4 = 26 6.19. Ефект впливу факторної ознаки на результативну визначається за: а) комбінаційним групуванням; б) аналітичним групуванням; в) рівнянням регресії. Відповіді: 1) а; 2) а, б; 3) б, в; 4) а, в. 6.20. Зв'язок між ступенем ризику об'єкта страхування та страховою ставкою можна описати рівнянням: 1) параболи; 2) гіперболи; 3) степеневим; 4) лінійним. 6.21. Зв'язок між урожайністю кукурудзи та кількістю атмосферних опадів можна описати рівнянням: 1) лінійним; 2) степеневим; 3) параболи; 4) гіперболи. 6.22. Зв'язок між річним споживанням м'яса та м'ясопродуктів (кг) та середньодушовим доходом населення за рік (гр. од.) описано рівнянням регресії: Y=36+0,02x. Це значить, що з підвищенням середньодушового доходу на 10 гр. од., споживання м'яса та м'ясопродуктів збільшиться в середньому на: 1) 20 г; 2) 200 г; 3) 2 кг; 4) 36,2 кг. Розв*язок: Y=36+0,02x=36 + 0,02*10 = 36,2 6.23. Зв'язок між процентною ставкою на міжбанківський кредит (%) та терміном надання кредиту (днів) описано рівнянням регресії: Y=18+0,5x. Це значить, що з подовженням терміну користування кредитом на 1 день процентна ставка збільшиться в середньому на: розв*язок: Y=18+0,5x = 18+0,5*1 = 18,5 1) 5%; 2) 18%; 3) 0,5%; 4) 18,5%. 6.24. Зв'язок між прибутком від звичайної діяльності підприємств (тис. гр. од.) та числом днів прострочених платежів описано рівнянням регресії: Y=100-0,4х. Це означає, що з кожним днем прострочених платежів прибуток від звичайної діяльності у середньому зменшуватиметься: 1) на0,4%; 2) у0,4 раза; 3) за відсутності платежів становить 99,6 тис.гр.од.; 4) за своєчасної сплати дорівнює 100 тис.гр.од. 6.25. Залежність між зростом дорослих людей (см) та їх вагою (кг) описана лінійним рівнянням регресії Y = 70 + 25x. помилково обчислені параметри: 1) а; 2) Ь; 3) а, Ь; 4) -. 6.26. Розмір пенсій за віком (гр.од.) певним чином залежить від загального стажу роботи пенсіонерів (років), що описано рівнянням регресії: Y=340-12x;. помилково обчислені параметри: 1) а; 2) Ь; 3) а, Ь; 4) –. 6.28. Якщо R^2= 1, тоді: а) лінія регресії проходить через усі емпіричні точки; б) лінія регресії проходить паралельно осі абсцис; в) зв'язок відсутній; г) зв'язок функціональний. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.29. Коефіцієнт детермінації характеризує: а) частку варіації факторної ознаки за рахунок результативної; б) частку варіації результативної ознаки, пов'язану з варіацією факторної. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.З0. Зв'язок між середнім балом успішності студентів на І курсі та оцінками на вступних іспитах оцінено коефіцієнтом детермінації, який становить 0,36. Це означає, що варіація успішності студентів пояснюється варіацією оцінок на вступних іспитах, у% на: 1) 64; 2) 60; 3) 36; 4) 40. Коефіцієнт детермінації показує, що 36% варіації середнього балу успішності студентів на І курсі залежить від варіації оцінок на вступних іспитах, а 64% припадає на інші фактори. 6.31. Лінійний коефіцієнт кореляції між середньодушовим доходом сім'ї та бажаною кількістю дітей становить0,4. Це означає, що варіація результативної ознаки пояснюється варіацією факторної, у% на: 1) 40; 2) 60; 3) 16; 4) 84. 6.32. Лінійний коефіцієнт кореляції між рівнем механізації робіт та продуктивністю праці дорівнює 0,6. Це означає, що варіація продуктивності праці пояснюється варіацією рівня механізації робіт, у% на: 1) 60; 2) 40; 3) 36; 4) 64. 6.33. Зв'язок між рівнем прибутковості активів та часткою високоліквідних активів оцінено за допомогою коефіцієнта детермінації, який становить 0,54. Це означає, що варіація частки високоліквідних активів пов'язана з варіацією прибутковості активів, у% на: 1 ) 54; 2) 46; або варіація прибутковості активів пов'язана з варіацією частки високоліквідних активів, у% на: 3) 54; 4) 46. 6.34. Про вік і середній виробіток робітників підприємства відомі такі дані: Номер групи робітників 1 2 3 4 5 6 7 8 Вік робітників, років 20 25 30 35 40 45 50 55 Середньоденний виробіток, гр. од. 18 22 25 31 34 38 46 52 Рівняння регресії, яке визначає залежність середньоденного виробітку від віку робітників має вигляд: а) Y = -2,45 + 0,952x; б) Y = 2,45 + 0,991x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,991; г) 0,952. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.35. Фондовіддача та продуктивність праці торговельних підприємств району характеризувалися в2006 р. такими даними: Номер торговельного підприємства 1 2 3 4 5 6 7 Фондовіддача, грн. 12 17 18 14 15 20 16 Продуктивність праці, тис. грн. 142 152 185 148 156 173 161 рівняння регресії, яке описує залежність продуктивності праці від фондовіддачі має вигляд: а) Y = 74,61+ 3,641x; б) Y = 84,61+ 4,685x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,817; г) 0,822. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.36. За даними аудиторського звіту про діяльність 9 комерційних банків встановлено таку залежність між розміром кредитної ставки та дохідністю кредитних операцій: Номер банку 1 2 3 4 5 6 7 8 9 Кредитна ставка, % 40 45 48 44 52 56 62 58 65 Дохідність від кредитних операцій, % 18 22 35 28 38 52 46 48 54 Функція, яка описує залежність між дохідністю від кредитних операцій і розмірами кредитних ставок має вигляд: а) Y = 36,123+ 1,417x; б) Y = 32,157+ 0,958x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,893; г) 0,937. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.37. При вибірковому спостереженні впливу кількості внесених мінеральних добрив на урожайність кормових культур у 10 фермерських господарствах одержано такі дані: Номер господарства 1 2 3 4 5 6 7 8 9 10 Внесено мінеральних добрив, ц/га 1,2 1,4 1,3 1,8 1,9 1,7 2,2 1,6 1,1 2,1 Урожайність, ц/га 24,6 25,8 24,1 30,2 28,3 31,4 35,4 26,3 25,4 36,2 Лінійне рівняння регресії, яке описує залежність урожайності кормових культур від кількості внесених мінеральних добрив має вигляд: а) Y = 11,657 + 10,499x; б) Y = 18,164+ 9,422x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,901; г) 0,807. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.38. Відомі такі дані про 10 комерційних банків: Номер банку 1 2 3 4 5 6 7 8 9 10 Кредитна ставка, % 34 45 28 54 36 42 38 52 41 30 Дохідність кредитних операцій, % 31 42 32 52 33 45 36 46 38 35 Рівняння однофакторної регресії, яке описує залежність дохідності кредитних операцій від кредитної ставки має вигляд: а) Y= 8,657+ 1,099x; б) Y= 9,51+ 0,737x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,961; г) 0,912. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.39. Відомі такі дані про підприємства лікеро-горілчаного виробництва: Номер підприємства 1 2 3 4 5 6 7 8 9 Фонд заробітної плати, тис. грн. 220 380 340 420 330 450 330 510 460 Обсяг випуску продукції, млн. грн. 85 160 150 180 140 210 140 250 190 Лінійне рівняння регресії, що описує зв'язок між фондом заробітної плати та обсягом випуску продукції має вигляд: а) Y = 78,06 + 1,819x; б) Y = 69,96 + 2,115x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,879; г) 0,979. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.40. Врожайність та собівартість вирощування цукрових буряків у фермерських господарствах регіону характеризуються такими даними: Номер фермерського господарства 1 2 3 4 5 6 7 8 9 10 Собівартість 1 ц, грн. 3,40 5,15 5,80 4,10 4,50 3,60 5,10 4,20 2,80 5,40 Врожайність, ц/га 220 210 170 280 230 320 420 310 300 450 Лінійне рівняння регресії, яке описує залежність собівартості вирощування цукрових буряків від урожайності має вигляд: а) Y = 4,22 + 0,000635x; б) Y = 3,43 + 0,135x, а значення лінійного коефіцієнта кореляції дорівнює: в) 0,060; г) 0,607. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.41. За даними аудиторської перевірки 24 комерційних банків, виявлено залежність між рівнем ліквідності активів та їх прибутковістю. Коефіцієнт Середній рівень Кількість банків ліквідності активів прибутковості активів, % 0,2 – 0,4 6 15 0,4 – 0,7 5 8 0,7 – 1,0 5 6 1,0 ібільше 8 3 Вцілому 24 7,7 Загальна дисперсія прибутковості активів дорівнює 31. Міжгрупова дисперсія дорівнює: а) 25,21; б) 21,31, а емпіричне кореляційне відношення: в) 813; г) 0,687. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.42. Коефіцієнт кореляції рангів використовують для оцінки щільності зв'язку між: а) кількісними ознаками; б) ознаками, значення яких можна упорядкувати; в) будь-якими атрибутивними ознаками. Відповіді: 1) а; 2) а, б; 3) б; 4) а, в.
6.43. За оцінками експертів ранги країн щодо їх політичної стабільності Rх та стану платіжного балансу Rу розподілилися так: Країна А В С D К М N Rх 1 3 2 4 7 6 5 Rу 2 3 1 5 6 7 4 Коефіцієнт рангової кореляції Спірмена становить: а) 0,107; б) 0,893. Критичнейогозначення 0.95 (7) 0.714. Зімовірністю 0,95: в) зв'язок визнається істотним; г) істотність зв'язку недоведена. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. Розв’язання: За оцінками експертів ранги країн щодо їх політичної стабільності Rx та стану платіжного балансу Ry розподілилися так:
6.44. На конкурсі краси судді розподілили місця між конкурсантками так: Номер 1 2 3 4 5 6 конкурсантки Суддя А 4 3 2 5 6 1 Суддя В 5 3 1 4 6 2 Ранговий коефіцієнт кореляції Спірмена як міра узгодженості оцінок судді встановить: а) 0,114; б) 0,886. Критичне його значення с0.95 (6) 0.828. З імовірністю 0,95 кореляція оцінок вважається: в) істотною; г) неістотною. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.45. Тестування членів туристичної групи дало такі результати: Номер туриста 1 2 3 4 5 6 7 Ранг за адаптаційним 2 3 4 1 7 5 6 тестом Ранг за тестом 3 1 4 2 6 5 7 диференціації Коефіцієнт рангової кореляції Спірмена становить: 1) 0,143; 2) 0,857. Критичне його значення с0.95 (6) 0.828. З імовірністю 0,95 нульова гіпотеза про відсутність зв'язку: в) відхиляється; г) не відхиляється. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.46. Коефіцієнт взаємної спряженості використовують для оцінки щільності зв'язку між ознаками, якщо: а) обидві ознаки атрибутивні; б) лише факторна ознака атрибутивна; в) лише результативна ознака атрибутивна; г) обидві ознаки кількісні. Відповіді: 1) а, б, в; 2) а, б, в, г; 3) а, б; 4) а. 6.47. Якщо коефіцієнт взаємної спряженості дорівнює нулю, то умовні розподіли результативної ознаки: а) збігаються; б) не збігаються. Факторна і результативна ознаки: в) залежні; г) незалежні. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.48. Для оцінки щільності зв'язку між альтернативними ознаками можна використати: а) коефіцієнт взаємної спряженості; б) коефіцієнт асоціації; в) характеристику ч. Відповіді: 1) а; 2) а, б; 3) а, б, в; 4) в. 6.49. За даними опитування 200 виборців розподіл їх за місцем народження та політичною прихильністю характеризується даними: Виборці За За лейбористів Разом консерваторів Корінні жителі 82 78 160 Іммігранти 10 З0 40 Разом 92 108 200 Коефіцієнт контингенції Пірсона становить: 1) 0,52; 2) 3,15; 3) 0,21; 4) 8,82. 6.50. За допомогою коефіцієнта контингенції Пірсона оцініть щільність зв'язку між сімейним станом та психологічними настроями новоприбулих до будинку для ветеранів. Сімейний стан Відчувають Не відчувають Разом самотність самотності Одинаки 15 25 40 Вдові, розлучені 40 20 60 Разом 55 45 100 Коефіцієнт контингенції становить: 1) -0,287; 2) 0,30; 3) -0,538; 4) 8,25.
6.51. Якщо у 4-клітинній таблиці умовні розподіли збігаються, тобто частки d11=d21, то відношення шансів: a) W=l; 2) W<1. Якщо умовні розподіли не збігаються, зокрема d21<d11,To: в) W<1; r) W>1. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г. 6.52. За минулий тиждень службою зайнятості працевлаштовано36 чоловік із 100 зареєстрованих безробітних. Розподіл працевлаштованих характеризується даними: Безробітні Праце- Непраце- Разом влаштовано влаштовано Вміють працювати з персо- 24 16 40 нальним комп'ютером Не вміють 12 48 60 Разом 36 64 100 Відношення шансів становить: а) 2; б) 6. Шанси працевлаштуватись осіб, що вміють працювати з комп'ютером, більші: в) у б разів; г) у2 рази. Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 3529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.222.30 (0.009 с.) |

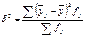

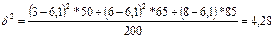
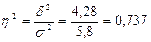
 Оскільки η2 > η2табл, то зв’язок істотний і доведений.
Оскільки η2 > η2табл, то зв’язок істотний і доведений.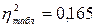 Оскільки η2 > η2табл, то зв’язок істотний і доведений
Оскільки η2 > η2табл, то зв’язок істотний і доведений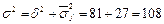
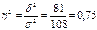
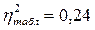 Оскільки η2 > η2табл, то зв’язок істотний і доведений
Оскільки η2 > η2табл, то зв’язок істотний і доведений


