
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до лабораторних занять з фізикиСодержание книги
Поиск на нашем сайте
ЗМІСТ
Ст. Вступ …………………………………………………........... 5 Методичні вказівки до лабораторних занять з фізики... 7 Правила обробки результатів вимірювання …………… 9 Вимірювальні прилади ……………………………………. 14 Лабораторна робота № 1 ………………………………… 22 Визначення швидкості руху тіла по похилій площині Лабораторна робота № 2 ………………………………… 25 Експериментальна перевірка другого закону Ньютона Лабораторна робота № 3 ………………………………… 29 Визначення моменту інерції тіла Лабораторна робота № 4 ………………………………… 32 Визначення швидкості польоту кулі за допомогою балістичного маятника Лабораторна робота № 5 ……………………………….…. 36 Визначення моменту інерції махового колеса Лабораторна робота № 6 ………………….…………….… 39 Перевірка основного рівняння динаміки обертового руху твердого тіла Лабораторна робота № 7 ………………………………..… 43 Визначення головних осей інерції Лабораторна робота № 8 ………………………………..… 48 Визначення швидкості кулі за допомогою крутильного балістичного маятника Лабораторна робота № 9 ………………………………..… 54 Визначення коефіцієнта тертя кочення Лабораторна робота № 10 ……………………………..… 59 Вивчення прецесії гіроскопа
Лабораторна робота № 11 ……………………………..… 64 Визначення моменту інерції тіла неправильної геометричної форми Лабораторна робота № 12 ……………………………..… 68 Визначення прискорення земного тяжіння і коефіцієнта жорсткості пружини за допомогою пружинного маятника Лабораторна робота № 13 ……………………………..… 72 Визначення швидкості звуку в повітрі Лабораторна робота № 14 ……………………………..… 76 Визначення прискорення вільного падіння за допомогою оборотного маятника Лабораторна робота № 15 ……………………………..… 82 Визначення логарифмічного декремента затухання, коефіцієнта затухання і добротності коливної системи
Перелік літературних джерел …………………………... 86
Додаток ……………………………………………………... 87
ВСТУП
Фізика є базовою дисципліною для багатьох загальноінженерних і спеціальних дисциплін. Процес пізнання у фізиці, як і в будь-якій науці, починається зі спостереження явищ в природних умовах або із спеціально поставлених дослідів-експериментів. Для вивчення явища експериментатор повинен володіти достатніми навиками проведення вимірювань, які набуваються в процесі навчання. Основними завданнями фізичного лабораторного практикуму є виховання у студентів навиків дослідницької роботи, якісного і кількісного вивчення фізичних явищ. До складу посібника увійшло 15 лабораторних робіт з методичними вказівками щодо їх виконання та оформлення звітів. Методичні вказівки призначені для допомоги студентам при виконанні лабораторних робіт з розділу «Механіка» і складені з навчальним планом і програмою з фізики. Виконання робіт покликане сприяти більш глибокому розумінню найважливіших законів класичної механіки, на основі яких вирішуються фізичні задачі і проблеми в обраній студентами спеціальності. Кожна лабораторна робота містить короткі теоретичні відомості, порядок виконання роботи, практичні завдання та запитання для самоконтролю, посилання на літературні джерела. Особлива увага звертається на найбільш повне розкриття фізичної суті досліджуваних явищ та змісту тих параметрів, якими ці явища описуються. Важливе питання – це точність вимірювання експериментальних результатів. Тому в посібнику описано методику проведення прямих і непрямих вимірювань різних фізичних величин та правила обробки результатів вимірювання із обчисленням похибок і записом остаточного результату.
МЕТОДИЧНІ ВКАЗІВКИ ДО ЛАБОРАТОРНИХ ЗАНЯТЬ З ФІЗИКИ
Основні правила безпеки роботи в лабораторії 2.1 Всі роботи в лабораторії виконуються тільки під керівництвом викладача або лаборанта. 2.2 Користуватися тільки справними приладами і інструментом. 2.3 Не загромаджувати робоче місце сторонніми предметами, які не відносяться до даної роботи. 2.4 Не ходити без потреби по лабораторії, не торкатись вузлів, приладів і інших предметів, які не відносяться до даної лабораторної роботи. 2.5 Не включати і не виключати без дозволу викладача рубильники, прилади, стенди, лабораторні установки. 2.6 Про всі помічені неполадки негайно повідомити викладача. 2.7 Забороняється під час заняття: - займатися без дозволу викладача усуненням неполадок в установці; - відволікати товаришів сторонніми розмовами; - виносити з лабораторії прилади, інструменти, деталі і т.д., а також вносити в лабораторію сторонні предмети.
У випадку порушення правил безпеки роботи в лабораторії, викладач зобов’язаний відсторонити студента від виконання лабораторної роботи.
ПРАВИЛА ОБРОБКИ РЕЗУЛЬТАТІВ ВИМІРЮВАННЯ
Обробляючи результати вимірювань, рекомендуємо дотримуватись такої послідовності дій.
А. Прямі вимірювання
1. Після виконання n вимірювань фізичної величини x дістають такі її значення: x 1, x 2, x 3, … xn. Кількість вимірювань n залежить від природи вимірюваної величини, точності застосовуваних для вимірювання інструментів і в кожному випадку визначається окремо. 2. Знаходять середнє арифметичне значення вимірюваної величини за формулою
(1)
3. Визначають випадкові абсолютні похибки вимірювання:
x - x, D x = x - x K . (2)
арифметичного за формулою D x 2 +D x 2 +K+D x 2 середнього
n (n - 1). (3)
6. За числом вимірювань і довірчою ймовірністю p в
(n). 7. Визначають півширину довірчого інтервалу випадкової похибки (тобто абсолютну випадкову похибку)
(n) S.
(4) 8. Визначають межу основної похибки d, яку допускає засіб вимірювання, згідно з його паспортом.
t (¥) для нескінченного числа вимірювань за даною довірчою ймовірністю p. 10. Визначають інструментальну похибку за формулою
t (¥)d .
(5)
11. Визначають межу похибки v відліку за шкалою приладу як половину ціни поділки. Таблиця 1
12. Визначають похибку відліку
D x відл = p v. (6)
13. Знаходять повну похибку вимірювання
D x = D x вип +D x ін +D x відл (7) 14. Визначають відносну похибку
X x
(8)
15. Записують кінцевий результат у вигляді
(9)
Приклад 1. Під час вимірювання довжини l бруска міліметровою лінійкою дістали чотири значення довжини: l 1 = 120, p = 0,96. l 2 = 119, l 3 = 121, l 4 = 120 мм, довірча ймовірність
Знаходимо середнє арифметичне значення вимірюваної довжини
l =
= 0,120.
Середня квадратична похибка дорівнює
l 4 × 3 = 4 × 10 - 4 м.
Із табл. 1 знаходимо
t 0,95 (4)= 3,2. Випадкова похибка
= 13 × 10 - 4 м. Інструментальна похибка
D l ін = 2 × 0,2 = 2,3 × 10 - 4
м (t
0,95
(¥)= 2,0, d = 0,2). Похибка відліку D l
Відл = 0,95 × 0,5 × 10 - 3 = 4,0 × 10 - 4 м.
Повна похибка вимірювання дорівнює
(132 + 2,32 + 4,82)× 10 - 4
= 2 × 10 - 3 м.
Записуємо кінцевий результат вимірювання довжини l =(120 ± 2)× 10 - 3 м з довірчою ймовірністю p = 0,95.
Б. Непрямі вимірювання
1. Якщо величина y, яку визначають, є функцією кількох змінних x 1, x 2, … xn, тобто , x 2 , K, xn), (10)
то для кожної з них потрібно визначити середнє арифметичне значення і повну абсолютну похибку.
2. Визначають середнє значення невідомої величини
, K, xn).
3. Знаходять відносну похибку за формулою
2 2
e y = ê ëê ¶ x 1
× D x 1 ú úû +ê ëê ¶ x 2
× D x 2 ú úû +K+ê êë
¶ xn
× D xn ú. úû
4. Визначають абсолютну похибку
5. Записують кінцевий результат у вигляді
з довірчою ймовірністю p.
Приклад 2. Визначити об’єм циліндра.
p d 2 h
де d – діаметр; h – висота циліндра. d =(20,00 ± 0,05)× 10 - 3 м, h =(10,00 ± 0,05)× 10 - 3 м.
Середній об’єм циліндра:
м3.
2 0,05 + 0,05
+ 0,005 3,14
D V = 6 × 10 - 3 × 3,14 × 10 - 6 = 0,02 × 10 - 6
Записуємо кінцевий результат у вигляді V =(3,14 ± 0,02)× 10 - 6 м 3.
м 3.
ВИМІРЮВАЛЬНІ ПРИЛАДИ
Масштабна лінійка Масштабні лінійки бувають одношкальні та двошкальні, жорсткі чи пружні з межами вимірювань 150 - 1000 мм. Шкала лінійок має ціну поділки 0,5 чи 1 мм, що дає похибку при вимірюваннях ~0,25 мм та ~0,5 мм відповідно. Для лінійних вимірювань з більш високою точністю застосовують штанґенциркулі, мікрометри, катетометри та ін.
Штанґенциркуль Щтанґенциркуль складається зі сталевої масштабної лінійки 1, яка поділена на сантиметри і міліметри (рис.1). На початку лінійки закріплені нерухомі губки 2. По лінійці переміщується
Рисунок 1.
звідки m × x = (m - 1)× x, x 0
Різниця між ціною поділки основної шкали і ціною поділки ноніуса називається точністю ноніуса:
- x = x 0. m Як бачимо, точність ноніуса дорівнює ціні поділки шкали масштабної лінійки, поділеної на число поділок ноніуса. Виберемо m = 10, а х 0 = 1мм. Якщо сумістити нульову поділку шкали такого ноніуса з нульовою поділкою основної шкали, 10-та поділка ноніуса виявиться суміщеною з 9-тою поділкою масштабної лінійки (рис.2а). При цьому 1-ша поділка ноніуса не дійде до 1-ї поділки лінійки на 0,1 мм, 2-га поділка ноніуса не дійде до 2-ї поділки шкали лінійки на 0,2 мм і т.д. (рис.2а). Шкали штанґенциркуля наносяться таким чином, що при зсунутих губках нуль шкали ноніуса і нуль основної шкали співпадають. При вимірюванні довжини штанґенциркулем предмет поміщають між губками, губки зсувають до стикання з предметом і закріплюють їх у такому
положенні ґвинтом 6; потім проводять відлік з допомогою ноніуса.
а) б)
L0 ΔL
Мм 5 10 L 0 n
Довжина предмета L дорівнює віддалі від нуля основної шкали до нуля зміщеного ноніуса і складається з цілого числа k поділок основної шкали L 0 = k · x 0 та деякої частини наступної поділки основної шкали – відрізка ΔL (рис.2б): L = L 0 +D L. Знаходимо поділку ноніуса (наприклад n), що співпадає з поділкою основної шкали (k + n), тоді: D L = n × x 0 - n × x = n ×D x. Отже,
L = k × x 0 + n × D x. Звідси випливає правило відліку довжини з допомогою ноніуса:
вимірювана довжина L дорівнює сумі числа малих поділок основної шкали (kx 0) і точності ноніуса D x, помноженої на номер n його поділки, яка співпадає з поділкою основної шкали.
Якщо при вимірюванні не виявиться жодної поділки ноніуса, яка співпадала би точно з поділкою основної шкали, то відлік береться по тій поділці, яка розміщена найближче до одної з поділок основної шкали масштабної лінійки. Величина
незбігання не перевищує половини точності ноніуса Δ x. Отже, похибка відліку по ноніусу дорівнює половині його точності.
Мікрометр На кінцях масивної стальної скоби 1 (рис.3) знаходяться один напроти одного нерухома опорна п’ята 2 і наконечник мікрометричного ґвинта 4. Ґвинт обертається у втулці 3, вздовж якої ззовні нанесена шкала з поділками через 0,5мм. На ґвинт насаджено барабан 5, край якого при обертанні ґвинта переміщається відносно шкали, нанесеної на втулці. По краю барабана нанесена шкала, яка ділить обвід барабана на 50 рівних поділок; крок ґвинта 0,5мм, отже ціна 1 поділки барабана 0,01мм, тобто поворот барабана на 1 поділку відповідає зміщенню ґвинта на 0,01мм.
Рисунок 3.
На кінці ґвинта є пристрій 6 для обертання барабана, який називається тріскачкою. Обертання передається від тріскачки до ґвинта завдяки тертю, внаслідок чого при досягненні певної сили натиску наконечника ґвинта на опорну п’яту чи на вимірюваний предмет подальше обертання ґвинта припиняється.
Якщо наконечник ґвинта і опорну п’яту звести разом, край барабану буде проти нульової поділки шкали, нанесеної на втулці, а нульова поділка шкали барабана співпадає з поздовжньою лінією, нанесеною на втулці.
Рисунок 4. Рисунок 5.
При роботі з мікрометром вимірюваний предмет затискається за допомогою тріскачки між опорною п’ятою та наконечником ґвинта, після чого по шкалі втулки відраховується ціле чи напівціле число міліметрів і до цього відліку додається число сотих часток міліметра, яке відраховується по шкалі барабана. Наприклад: - на рис.4. відлік становить 6,40 мм, оскільки на шкалі втулки вкладається ціле число 6 мм, а на шкалі барабана - 40 сотих мм; - на рис.5. відлік становить не лише 6 цілих мм, але ще й одну поділку за верхньою шкалою півцілих мм, тому показ шкали втулки – 6,5 мм. Якщо додати 40 сотих мм, які відраховує шкала барабана, то повний відлік буде 6,90 мм. Перед вимірюваннями мікрометром потрібно переконатися у тому, що при доведенні тріскачкою наконечника ґвинта до опорної п’яти отримується на обох шкалах нульовий відлік.
Вимірювання часу При вимірюванні невеликих проміжків часу користуються секундомірами: механічними, електричними та електронними. Електричний секундомір має на циферблаті дві колові шкали. Зовнішня, більша, визначає десяті та соті частки секунди, а внутрішня, менша – цілі секунди. Ввімкнення і вимкнення приладу проводиться вимикачем, розміщеним на столі поряд із секундоміром. Повернення стрілок у нульове положення проводиться натисканням металевого стрижня на правій бічній поверхні корпусу секундоміра. Електронний секундомір відображає вимірювані проміжки часу на електронному табло до сотих часток секунди. На передній панелі секундоміра знаходяться вертикально розміщені три клавіші. Верхня призначена для під’єднання секундоміра до електромережі, середня – для вимірювання часу, а нижня – для занулення показів приладу. Точність для секундомірів з ручним вмиканням приймається рівною 0,2 секунди. Це зумовлено тим, що людина не може роздільно сприймати проміжки часу, менші за 0,1 секунди. Тому при вимірюваннях експериментатор буде допускати помилки незалежно від точності секундоміра: у момент ввімкнення ±0,1 с, у момент вимкнення також ±0,1 с. Отже, максимальна похибка становитиме ±0,2 с.
Вимірювання температури Для вимірювання температури використовують такі фізичні властивості речовин, які однозначно змінюються при зміні температури і легко можуть бути виміряні. Це: лінійне і об’ємне розширення, зміна тиску, виникнення термоелектрорушійної сили, зміна електричного опору, деякі магнітні та оптичні властивості.
Відлік температур здійснюють за температурними шкалами: термометричній (наприклад, шкала Цельсія) і термодинамічній (шкала Кельвіна). Для побудови термометричної шкали вибирають дві постійні температури (реперні точки). Наприклад, за 0 приймають температуру плавленні льоду і за 100 - температуру кипіння води при нормальному тиску. Якщо у цьому температурному інтервалі вимірювати величину об’ємного розширення ртуті, яка знаходиться у балоні, що з’єднаний з капіляром, то, поділивши видовження ртутного стовпа у капілярі на 100 рівних частин, отримаємо шкалу Цельсія (°С). Побудова термодинамічної температурної шкали ґрунтується на другому законі термодинаміки. Одиницею вимірювання у ній є кельвін (К). Ґрадус за шкалою Кельвіна встановлюють так, щоби мала місце узгодженість зі шкалою Цельсія і для практичних вимірювань використовується співвідношення: T (K)= t (° C)+ 273,15 (° C). Вимірювання температури до 600 °С називається термометрією, а вище 600 °С - пірометрією. Прилади для вимірювання температури діляться на такі групи: Термометри розширення (до 750 °С) побудовані на властивостях тіл при зміні температури змінювати свій об’єм, а значить і лінійні розміри. Манометричні (газові) термометри (до 500° С) заповнені розрідженим газом (воднем, гелієм чи азотом). За зміною тиску термометричного газу у термометрі при постійному об’ємі можна виміряти його температуру. Електричні термометри опору (до 500 °С) визначають температуру за зміною опору давача: мідного або платинового опору. Термоелектричні (термопарні) термометри (до 1600 °С) використовують властивості контактів різних металів та
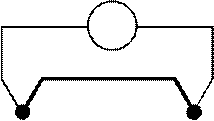
сплавів. Термопарою називається замкнене електричне коло, яке має два спаї різних металевих провідників (наприклад, мідь-константан, хромель-копель і т.д.) (рис.6).
T1 T2 Рисунок 6.
Якщо температура спаїв різна (Т 1> Т 2), то у колі протікає електричний струм зумовлений термоелектрорушійною силою. Виміряна мілівольтметром величина електрорушійної сили Е пропорційна різниці температур:
E = c ×(T - T)= c ×(t 0C - t 0C), 1 2 1 2
де с - постійна величина, різна для різних термопар. Один спай термопари щільно притискають до тіла з невідомою температурою, а температуру другого спаю підтримують постійною (наприклад t 2°C = 20°C). Визначення температури тіла t 1°C за величиною виміряної E здійснюють з використанням ґрадуювальних таблиць.
Лабораторна робота № 1
Теоретичні відомості
Якщо тіло скочується з похилої площини і відривається від неї в точці В, то далі воно буде рухатись по параболі, доки A
H l В Vx D b V
О x C
Рисунок 1.1 не впаде в точці С (рис.1.1). Рух по параболі можна розглядати як такий, що складається з двох рухів: по вертикалі і горизонталі. Згідно з принципом незалежності рухів рух по вертикалі не залежить по вертикалі, не залежить від руху по горизонталі. Рух по горизонталі буде рівномірним з швидкістю vx = v 0 × cos a, а рух по вертикалі – рівноприскореним з початковою швидкістю тяжіння g. v y = v 0 sin a і прискоренням земного Позначимо шлях ОС, пройдений в горизонтальному русі буквою х, а шлях ВО в вертикальному русі буквою у і запишемо їх рівняннями:
.
(1.1) Розв’язавши систему рівнянь, визначимо швидкість руху тіла в момент відриву від похилої площини:
cos a g
. (1.2)
З рис.1 видно, що cosa= b, а
tg a= h. З врахуванням b останніх співвідношень одержимо формулу для швидкості
g × b
. (1.3)
Швидкість тіла, що котиться по похилій площині можна визначити і теоретично. В точці А (див. рис.1.1) тіло має потенціальну енергію, яка відносно рівня DВ рівна: E p = mgh. В точці В ця потенціальна енергія перетвориться в кінетичну енергію поступального і обертового руху тіла, запишемо закон збереження механічної енергії:
mgh = mv 2 +
I w 2
, (1.4) де v - швидкість поступального руху, w - кутова швидкість обертового руху, I - момент інерції тіла. Знаючи, що ω = v/R (де R – радіус тіла), визначимо v з рівняння (1.4) за формулою
mR 2
. (1.5)
Момент інерції тіла обертання можна записати у вигляді I = kmR 2, (1.6)
де R - радіус тіла. Для кулі k = 2/5, для суцільного циліндра k = 1/2, для кільця, в якого товщина набагато менша за радіус, k = 1. З врахуванням (1.6) формула (1.5) набирає вигляду
1 + k
. (1.7)
Слід зауважити, що у випадку товстостінного кільця з зовнішнім радіусом R і внутрішнім r, момент інерції m (R 2 + r 2)
вигляду
v = 2 h
3 R 2 + r 2
. (1.7′)
Порядок виконання роботи
1. Виміряти для похилої площини h,b,l, а також у, тобто висоту краю площини над поверхнею столу. 2. Помістити тіло на похилу площину на висоту h від основи і відпустити. Знайти точку С, в яку впаде тіло, і виміряти х. 3. Дослід повторити декілька разів, кожного разу пускаючи тіло з однієї і тієї же точки. 4. Визначити за формулою (1.3) і (1.7) або (1.7′) значення швидкості, обчислити похибки та порівняти одержані значення швидкостей.
Контрольні запитання
1. В чому полягає принцип незалежності рухів? 2. Що називається швидкістю і прискоренням точки? 3. Записати рівняння рівнозмінного руху. 4. Чому дорівнює кінетична енергія тіла, що котиться? 5. Вивести формулу для експериментального і теоретичного значень швидкостей.
Лабораторна робота № 2
Теоретичні відомості
Рисунок 2.1 Другий закон Ньютона, як відомо, встановлює співвідношення
між силою, масою і прискоренням. Прискорення, з яким рухається тіло, прямопропорційне силі і оберненопропорційне масі тіла: r
m Прискорення - фізична величина яка характеризує зміну швидкості з часом. Сила - міра взаємодії тіл, в результаті якої змінюється швидкість тіла, тобто виникає прискорення або тіла деформуються. Маса тіла - міра інертності тіла при поступальному русі. Якщо маса тіла m стала, то рівняння (2.1) можна написати у вигляді v r
де k = 1/ m. a = k × F, (2.2) Графічно залежність між a і F виразиться прямою, яка приходить через початок координат (а і F) і нахилена до осей під кутом, величина якого залежить від k, тобто від маси тіла.
графік в координатах F, а. Дослідити залежність а від F при O
T T B
Рисунок 2.2 сталій масі тіла можна з допомогою установки РМ-02 (машина Атвуда). Нехай до кінців нитки, перекинутої через блок, підвішені вантажі А і В (рис. 2.2) причому m 2 > m 1. Рівнодійна сил, що діють на систему не дорівнює нулю і заставляє систему рухатись прискорено. Рівняння руху системи у векторній формі, у випадку нехтування тертям і масою блока, запишуться так:
m g + T = m a, 1 r 1 (2.3) m g r+ T = m a r. 2 2
Рівняння (2.3) в проекціях, з врахуванням напряму руху, матимуть вигляд: T - m g = m a, 1 1 (2.4) T - m g =- m a. 2 2
Розв'язавши систему (2.4) відносно а, одержимо
. (2.5)
З (2.5) видно, що при сталій масі, прискорення, з яким рухаєтеся система, залежить від різниці мас m 2 - m 1 підвішених до кінців н
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.014 с.) |

 При підготовці даного посібника були використані методичні вказівки до п'ятнадцяти лабораторних робіт, підготовлених у 1997 році викладачами кафедри фізики Б.Ю. Самелюком, В.В. Омельяненком, В.І. Пустоговим, А.Г. Калугіним, З.В. Петрук.
При підготовці даного посібника були використані методичні вказівки до п'ятнадцяти лабораторних робіт, підготовлених у 1997 році викладачами кафедри фізики Б.Ю. Самелюком, В.В. Омельяненком, В.І. Пустоговим, А.Г. Калугіним, З.В. Петрук.

 x = x 1 + x 2 + x 3 +K+ xn.
x = x 1 + x 2 + x 3 +K+ xn.


 4. Оцінюють середню квадратичну похибку S x
4. Оцінюють середню квадратичну похибку S x 1 2 n
1 2 n Sx =
Sx =
 3
3 2 2 2.
2 2 2. e =D x.
e =D x. x =(x ±D x).
x =(x ±D x).
 (120 + 119 + 121 + 120)× 103
(120 + 119 + 121 + 120)× 103
 = 10 - 3 × =
= 10 - 3 × = 3
3 D l =
D l =


 , x 2
, x 2 é¶(ln y)
é¶(ln y) ù é¶(ln y)
ù é¶(ln y) ù é¶(ln y) ù
ù é¶(ln y) ù x = x 1
x = x 1
 x = x 2
x = x 2 x = xn
x = xn D y =e y × y.
D y =e y × y. V =,
V =,

 e V =
e V = 10
10 = 0,006.
= 0,006.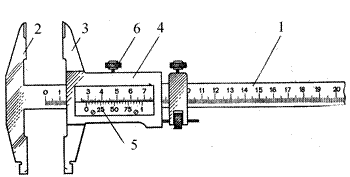 рамка 4, яка складає одне ціле з губками 3. Ці губки паралельні до губок 2 та можуть підходити до них впритул. Рамку можна закріпити у потрібному положенні ґвинтом 6.
рамка 4, яка складає одне ціле з губками 3. Ці губки паралельні до губок 2 та можуть підходити до них впритул. Рамку можна закріпити у потрібному положенні ґвинтом 6. x = x 0 - m.
x = x 0 - m. D x = x 0
D x = x 0 0 5 10
0 5 10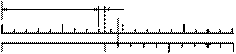 k k+1 k+n
k k+1 k+n Рисунок 2.
Рисунок 2.

 mV
mV Vy
Vy gt 2
gt 2 v = x
v = x
 2 (y - x × tg a)
2 (y - x × tg a) l
l v = l × x b
v = l × x b
 2(y × b - x × h)
2(y × b - x × h) 2
2 v = 2 gh
v = 2 gh 1 + I
1 + I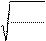 v = 2 gh
v = 2 gh I =. У цьому випадку формула (1.5) набирає
I =. У цьому випадку формула (1.5) набирає gh
gh a r= F. (2.1)
a r= F. (2.1) Таким чином, для дослідної перевірки закону Ньютона потрібно для декількох значень діючої на тіло сили, при заданій масі, визначити а і F, побудувати
Таким чином, для дослідної перевірки закону Ньютона потрібно для декількох значень діючої на тіло сили, при заданій масі, визначити а і F, побудувати A m2g m1g
A m2g m1g a = (m 2 - m 1) g m 2 + m 1
a = (m 2 - m 1) g m 2 + m 1


