
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення логарифмічного декрементаСодержание книги
Поиск на нашем сайте
ЗАГАСАННЯ, КОЕФІЦІЄНТА ЗАГАСАННЯ І ДОБРОТНОСТІ КОЛИВНОЇ СИСТЕМИ
Мета роботи: ознайомитись із затухаючими коливаннями системи і визначити її параметри: логарифмічний декремент загасання, коефіцієнт загасання і добротність. Обладнання: коливна система з самописцем і стрічко- протяжним механізмом, секундомір.
Теоретичні відомості
Якщо систему вивести з положення рівноваги і залишити саму на себе, то вона буде знаходитись під дією квазіпружної сили і сили опору. На подолання сили опору система при русі повинна затрачати енергію, отже амплітуда коливань системи весь час буде зменшуватися. Коливання будуть загасаючими. Рівняння загасаючих коливань має вигляд:
де A 0 e-βt – амплітуда загасаючих коливань, β – коефіцієнт загасання, ω = 2 πυ – циклічна частота (кругова частота), t – час, φ – початкова фаза коливань. Швидкість затухання характеризується за допомогою логарифмічного декременту загасання. Логарифмічним декрементом загасання називається натуральний логарифм відношення попередньої амплітуди до наступної, розділених інтервалом часу в один період Т:
A e -b t
A e
Проведемо перетворення:
e - b t
= ln e b T =b T.
Отже, e -b t e -b T
d=b T. (15.3)
З врахуванням (15.3) рівнянню (15.1) можна надати вигляду
T Визначити логарифмічний декремент загасання можна наступним чином. Нехай система здійснила N коливань при цьому амплітуда зменшилась в k разів. Отже:
T
(t +
NT)
= k. (15.5) A 0 e T Розв'язуючи це рівняння, знайдемо:
N З рівняння (15.3), знаючи δ і Т, можна знайти:
T
. (15.7) Відомо, що добротністю коливної системи називають величину Q, яка дорівнює π / δ. Отже
d Врахувавши (15.6) маємо:
ln k
. (15.9) За формулою (15.9) визначають добротність системи.
Порядок виконання роботи
1. Не вмикаючи самописець, відхилити маятник від положення рівноваги на кут 10°, відпустити його і секундоміром засікти час t декількох коливань n. Знайти період
n
(15.10)
A2 A b c
Рисунок 15.1 2. Коли маятник знаходиться в рівновазі, ввімкнути стрічкопротяжний механізм на 1-2 с. Самописець накреслить пряму ab, що відповідає положенню рівноваги (лінія ab на рис.15.1). 3. Відвести маятник від положення рівноваги, відпустити його і одночасно ввімкнути стрічко протяжний механізм. Записують коливання до повної зупинки маятника. 4. Вирізати частину стрічки з записом коливань. Продовжити за допомогою лінійки пряму ab, щоб одержати лінію, яка відповідає положенню рівноваги (пряма abc на рис. 15.1). 5. Виміряти лінійкою значення двох амплітуд (амплітуди А 1 і A 2 6. Підрахувати на записаній кривій за скільки коливань N амплітуда зменшилась від А1 до А2. 7. За формулою (15.6) визначити δ, а за формулою (15.8) – добротність системи. 8. Підставити у формулу (15.7) значення δ з (15.6) і Т з (15.10) одержати формулу для коефіцієнта загасання
Nt
і обчислити коефіцієнт загасання.
Контрольні запитання
1. Які коливання називаються загасаючими? 2. Запишіть диференціальне рівняння загасаючих коливань. 3. Чому дорівнює амплітуда загасаючого коливання? 4. Що називається логарифмічним декрементом загасання? 5. Що характеризує коефіцієнт загасання? 6. Що називається добротністю коливної системи?
Перелік літературних джерел
1. Кучерук І.М. Загальний курс фізики т.1 / І.М. Кучерук, І.Т. Горбачук, П.П. Луцик. – К.: Техніка, 1999. 2. Савельєв И.В. Курс общей физики / И.В. Савельєв. – М.: Наука, 1978. 3. Гапчин Б.М. Молекулярна фізика. Лабораторний практикум/ Б.М. Гапчин, Я.Й. Дутчак, В.С. Френчко. – Львів, 1990. 4. Булкин П.С. Общий физический практикум. Молекулярная физика/ П.С. Булкин, Н.Н. Попова. – М., 1988.
Додаток Основні фізичні сталі Гравітаційна стала γ = 6,672·10-11 м3/кг·с2 Універсальна газова стала R = 8,314510 Дж·моль-1·К-1 Стала Больцмана k = 1,380662 ·10-23 Дж·К-1 Стала Авогадро NA = 6,022045·1023 моль-1· Число Лошмідта NL = 2,686754·1025 м-3 Маса спокою електрона m e = 9,109534·10-31 кг Маса спокою протона m p = 1,6726231·10-27 кг Маса спокою нейтрона m n = 1,6749286·10-27 кг Елементарний електричний заряд e = 1,60217733·10-19 Кл Атомна одиниця маси а.о.м. = 1,6605655·10-27 кг Швидкість поширення світла у вакуумі с = 2,99792458·108 м/с Електрична стала ε0 = 8,85418782·10-12 Ф/м Магнітна стала μ0 = 4π·10-7 Гн·м Стала Планка h = 6,626176·10-34 Дж·с Число Фарадея F = 9,648456·104 Кл/моль
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.007 с.) |


 d= ln
d= ln
 -d t
-d t A 0 e
A 0 e -d
-d d= ln k. (15.6)
d= ln k. (15.6) b=d
b=d Q =p. (15.8)
Q =p. (15.8) Q =p N
Q =p N T = t.
T = t.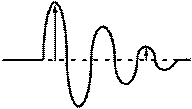
 b= n ln k. (15.11)
b= n ln k. (15.11)


