
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единицы измерения давления. Абсолютное давления. Вакуум.Содержание книги
Поиск на нашем сайте
До настоящего времени единицей измерения давления используется техническая атмосфера, равная давлению в 1 кгс на 1 см². Техническая атмосфера обозначается ат или кгс/см². В качестве единиц измерения давления применяют также метр и миллиметр водяного столба и миллиметр ртутного столба. Соотношения между этими единицами таковы: 1 кгс/см² = 735,56 мм рт. ст. (при 0 °С); В науке, а иногда и в технике за единицу давления принимается физическая атмосфера, обозначаемая атм и равная давлению столба ртути высотой 760 мм рт. ст. при 0 °С. Соотношения между технической и физической атмосферами следующие: 1 кгс/см² = 0,9678 атм; В системе СИ основной единицей измерения давления является Паскаль (Н/м²). Так как величина паскаль для практических целей часто слишком мала, то допускается применение внесистемной единицы давления — бар, которая равна 100 000 Па. Абсолютное давление pабс - это сумма атмосферного давления pатм и избыточного давления pизб. В полном вакууме, абсолютное давление равно 0 бар абс. В атмосфере на уровне моря, абсолютное давление составляет 1 бар абс. Pабс=Ратм+Ризб Ва́куум — среда, содержащая газ при давлениях значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного пробега молекул газа λ и характерным размером процесса d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т.д. В зависимости от величины соотношения λ/d различают низкий (λ/d<<1), средний (λ/d~1) и высокий (λ/d>>1) вакуум. На практике сильно разреженный газ называют техническим вакуумом. Под физическим вакуумом в современной физике понимают полностью лишённое вещества пространство.
Уравнение Д.Бернули для элементарной струйки. Для двух произвольных сечений и потока идеальной жидкости уравнение Бернулли имеет следующий вид:
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии: z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях;
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна. Уравнение Бернулли можно истолковать и чисто геометрически. каждый член уравнения имеет линейную размерность. z1 и z2 - геометрические высоты сечений над плоскостью сравнения; В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная. Уравнение Бернулли для реальной жидкости будет иметь вид:
в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости (α = 2 для ламинарного режима, α = 1 для турбулентного режима). Потерянная высота
Классификация видов движения жидкости. Движение жидкости может быть 2 видов: ламинарный режим и турбулентный. При ламинарном режиме отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой, а частицы жидкости движутся прямолинейно по параллельным друг другу траекториям. При этом режиме движения скорости в каждой точке потока не изменяются во времени ни по величине, ни по направлению. Наблюдается в тонких капиллярных трубках. Турбулентный режим характерно постоянное перемешивание жидкости и изменение во времени местных скоростей потока по величине и направлению – пульсацией скоростей; при этом частицы жидкости движутся по сложным и все время изменяющимся траекториям.
|
|||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.56.35 (0.009 с.) |


 - удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;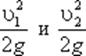 - удельные кинетические энергии в тех же сечениях.
- удельные кинетические энергии в тех же сечениях. - пьезометрические высоты;
- пьезометрические высоты; 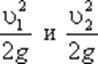 - скоростные высоты в указанных сечениях.
- скоростные высоты в указанных сечениях.
 складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями
складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями


