
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольно-обучающая программа №58.Содержание книги
Поиск на нашем сайте
Урок № 12 Таблица-матрица Законов математики и физики Таблица Матрица так же имеет четверичную систему построения и свой атом - функцию Y=X и отношения – комбинаторику степеней независимойпеременной.Это система вихря, который интенсивно взаимодействует с окружающей средой, что демонстрируют вихревые гиперболические воронки Геометрия Эвклида Древнегреческий математик Эвклид жил в 3 веке до н.э. Он написал трактат «Начала», в котором рассматривал элементарную геометрию. Постулаты геометрии Эвклида чрезвычайно просты: 1. Из каждой точки ко всякой другой точке, можно провести прямую. 2.Каждую ограниченную прямую можно продлить неопределенно. 3. Из любого центра можно описать окружность любого радиуса. 4. Все прямые углы равны. 5. И если прямая, падающая на две прямые, образуют внутренние углы и по одну сторону углы, меньше двух прямых, то продолженные эти прямые не ограничено встретятся с той стороны, где углы меньше двух прямых. Пятый постулат оказался самым знаменитым. Существуют десятки эквивалентных формулировок, доказательств, опровержений и они привели к тому, что появились геометрии Лобачевского, Римана и даже Абсолютная геометрия. Рассмотрим пятый постулат. A a b B c d рис.№17. Прямые А, В параллельны, если угол Особенностью геометрии Эвклида является тот факт, что сумма углов треугольника равна 180 Треугольники Треугольник – фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков попарно соединяющие эти точки. Точки называются вершинами треугольника, отрезки сторонами. Треугольники бывают равнобедренные, равносторонние, прямоугольные и разносторонние.
А С А С А С А С Прямоугольный Равносторонний Равнобедренный Разносторонний Рис № 18. рис № 19. рис №20. рис №21. 1. В равнобедренном треугольнике углы при основании равны. 2. В равностороннем треугольнике все углы равны друг другу. 3. В прямоугольнике один угол прямой. 4. В равностороннем все углы равные 5. Высотой треугольника называется прямая, проведенная из любого угла на противолежащую сторону так, что она делит угол пополам. 6. Биссектрисой треугольника называется прямая, проведенная из любого угла на противолежащую сторону так, что она делит угол пополам. 7. Медианой треугольника называется прямая, проведенная из любого угла на противолежащую сторону так, что она делит эту сторону пополам. (см. рис.№) Площадь треугольника 1. Площадь треугольника равна половине произведения его стороны на проведенную к ней высоту: S = 2. Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними: S = Контрольно-обучающая программа №58.
1. Треугольник имеет вершину и две стороны. 2. Треугольник имеет три угла и три стороны. 3. Все углы разные, если треугольник прямоугольный. 4. Все углы равны, если треугольник равносторонний 5. Любая высота является биссектрисой и медианой. 6. Любая медиана делит сторону пополам. 7. Треугольники бывают только остроугольные. 8. В равностороннем треугольнике высота всегда делит угол и сторону пополам. 9. В равностороннем треугольнике достаточно знать высоту и основание, чтобы найти стороны треугольника. 10. Длина гипотенузы равна сумме длин квадратов катетов.
Четырехугольники Четырехугольником - называется фигура, которая состоит из четырех точек и последовательно соединяющих отрезков. Точки называются вершинами, а отрезки –сторонами. При этом на одной прямой может лежать только две точки, а отрезки не должны пересекаться. Четырехугольники бывают: Параллелограммы, прямоугольники, квадраты, трапеции. B C B B C B C B C A C A A D D A D A D A D Параллелограмм 1. Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. 2. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
3. У параллелограмма противолежащие стороны и противолежащие углы равны. Ромб 1. Ромб – это параллелограмм, у которого все стороны равны. 2. Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов. Площадь параллелограмма Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне: S = ah Площадь ромба равна половине произведений его диагоналей:
Прямоугольник Прямоугольник - это параллелограмм, у которого все углы прямые. Если стороны a, b, то площадь S = ab. Квадрат – это параллелограмм, у которого все стороны равны и углы прямые. Если сторона равна а, то площадь S = Трапеция Трапеция – это четырехугольник, у которого два основания, которые параллельны и две боковые стороны, которые не параллельны. 1. Средняя линия трапеции параллельна основаниям и равна их полусумме. 2. У равнобедренной трапеции углы при основании равны.
Площадь трапеции Площадь трапеции равна произведению полусуммы ее оснований на высоту S = Таблица №9
0 R
Рис. №31. Параболическая геометрия Параболической геометрии как таковой нет. Никто не определял ее как геометрию. Нет постулатов, аксиом и сама поверхность, на которой реализована параболическая геометрия, не прописана. Параболоид построить конечно можно, но, как геометрическую поверхность его никто не рассматривал. Парабола, окружность и гипербола, могут быть отнесены к геометрии Эвклида если их рассматривать на плоскости, что и сделал Эвклид в третьем постулате своей геометрии указав, что из любого центра можно описать окружность, любого радиуса. Параболическую геометрию просто отнесли к геометрии Эвклида как плоскостную фигуру и считали, что к положительной кривизне и отрицательной она не относится. Однако анализ привел нас к выводу, что параболическая фигура имеет уравнение второй степени, и она может быть отнесена к геометриям, кривизна которых положительна. Все параболические функции делятся на чётные и нечётные (см. рис), нас интересуют только четные, они занимают промежуточное положение между прямой и окружностью (см. рис.№32.).

Рис. №32. Уравнения четной параболы второй степени играют заметную роль в системе четверичной логики. Четверичная логика определяет порядок и место совершаемых процессов при построении систем. В нашем случае функция прямой заменяется параболой, затем уравнением окружности. При повороте окружности перпендикулярно к оси «у», получаем гиперболу, что и демонстрирует вихрь (см. рис №32). Геометрия Римана. Геометрия Римана была опубликована в 1854 году. Это была третья великая геометрия после геометрии Эвклида и Лобачевского. Геометрия Эвклида царствовала в мире двадцать один век. Это была планиметрия (геометрия на плоскости). В 1832 году Лобачевский нанес ей тяжелый удар своей гиперболической геометрией, но она еще устояла 18 лет, пока эллиптическая геометрия Римана завершила ее царствование. Ученые поняли, что мир не является плоскостным и перестали обсуждать достоинства и проблемы геометрии Эвклида.
Мы широко применяем понятие геометрии Эвклида, Лобачевского, Римана, но необходимо отметить, что они никакого глубокого отношения к нам не имеют. Это великие творения чистого разума, и у нас нет никаких человеческих сил подняться до этих вершин. Почему же мы так решительно применяем эти понятия. Все дело в том, что эти творения дали нам возможность уйти от чистого разума в сторону реальной действительности и увидеть, как деформация пространства создает и меняет мир. Геометрия Римана реализуется на поверхности с постоянной положительной кривизной, т.е. на сферах. Она называется эллиптической в отличие от сферической (поверхности шара). В ней нельзя провести к прямой ни одной параллельной. В геометрии Римана сумма углов треугольника больше двух прямых. Проекция геометрии Римана на плоскость, как и сферической геометрии, дает окружность, x2 + y2 = R2.
Рис. №33. Для построения нашей стратегии, изложения математики и физики средней школы мы пользуемся алгебраическими и геометрическими осколками (проекциями) приводимых геометрий. В отличие от геометрий, осколки значительно ближе к реальности и мы путем структурирования и синтезирования пытаемся построить практические модели движения поля и вещества в рамках изложенных в учебниках законов, например: Геометрия Лобачевского Геометрия Лобачевского была опубликована на 18 лет ранее геометрии Римана. Она реализована на поверхности псевдосфер, кривизна которых отрицательна.
Рис №34. Мы многократно приводили ее рисунки и геометрические проекции. Особенностью является, то, что сумма углов треугольника на гиперболической поверхности меньше двух прямых. Геометрия называется гиперболической. Алгебраическая запись гиперболы: у = Внешний вид эллипсоида и гиперболоида привел нас к предположению, что эти геометрии были созданы чистым разумом, как проекции в разуме человека реальной действительности именно вихря. Это предположение руководит нашим анализом и синтезом при толковании учебного материала по математике и физики средней школы. Урок № 12 Таблица-матрица Законов математики и физики Таблица Матрица так же имеет четверичную систему построения и свой атом - функцию Y=X и отношения – комбинаторику степеней независимойпеременной.Это система вихря, который интенсивно взаимодействует с окружающей средой, что демонстрируют вихревые гиперболические воронки
Геометрия Эвклида Древнегреческий математик Эвклид жил в 3 веке до н.э. Он написал трактат «Начала», в котором рассматривал элементарную геометрию. Постулаты геометрии Эвклида чрезвычайно просты: 1. Из каждой точки ко всякой другой точке, можно провести прямую. 2.Каждую ограниченную прямую можно продлить неопределенно. 3. Из любого центра можно описать окружность любого радиуса. 4. Все прямые углы равны. 5. И если прямая, падающая на две прямые, образуют внутренние углы и по одну сторону углы, меньше двух прямых, то продолженные эти прямые не ограничено встретятся с той стороны, где углы меньше двух прямых. Пятый постулат оказался самым знаменитым. Существуют десятки эквивалентных формулировок, доказательств, опровержений и они привели к тому, что появились геометрии Лобачевского, Римана и даже Абсолютная геометрия. Рассмотрим пятый постулат. A a b B c d рис.№17. Прямые А, В параллельны, если угол Особенностью геометрии Эвклида является тот факт, что сумма углов треугольника равна 180 Треугольники Треугольник – фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков попарно соединяющие эти точки. Точки называются вершинами треугольника, отрезки сторонами. Треугольники бывают равнобедренные, равносторонние, прямоугольные и разносторонние.
А С А С А С А С Прямоугольный Равносторонний Равнобедренный Разносторонний Рис № 18. рис № 19. рис №20. рис №21. 1. В равнобедренном треугольнике углы при основании равны. 2. В равностороннем треугольнике все углы равны друг другу. 3. В прямоугольнике один угол прямой. 4. В равностороннем все углы равные 5. Высотой треугольника называется прямая, проведенная из любого угла на противолежащую сторону так, что она делит угол пополам. 6. Биссектрисой треугольника называется прямая, проведенная из любого угла на противолежащую сторону так, что она делит угол пополам. 7. Медианой треугольника называется прямая, проведенная из любого угла на противолежащую сторону так, что она делит эту сторону пополам. (см. рис.№) Площадь треугольника 1. Площадь треугольника равна половине произведения его стороны на проведенную к ней высоту: S = 2. Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними: S = Контрольно-обучающая программа №58.
1. Треугольник имеет вершину и две стороны. 2. Треугольник имеет три угла и три стороны.
3. Все углы разные, если треугольник прямоугольный. 4. Все углы равны, если треугольник равносторонний 5. Любая высота является биссектрисой и медианой. 6. Любая медиана делит сторону пополам. 7. Треугольники бывают только остроугольные. 8. В равностороннем треугольнике высота всегда делит угол и сторону пополам. 9. В равностороннем треугольнике достаточно знать высоту и основание, чтобы найти стороны треугольника. 10. Длина гипотенузы равна сумме длин квадратов катетов.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.232.145 (0.013 с.) |

 . Данную группу функций мы называем матрицей т.к. она соответствует четырем геометриям и 20 законам физики (см.таб.№ 4).
. Данную группу функций мы называем матрицей т.к. она соответствует четырем геометриям и 20 законам физики (см.таб.№ 4). а =
а =  ,
,  ah
ah
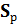 =
= 
 ; D – диагонали
; D – диагонали
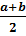 h
h ah; a – сторона; h – высота
2. Площадь четырёхугольника: S = ah
3. Площадь трапеции: S =
ah; a – сторона; h – высота
2. Площадь четырёхугольника: S = ah
3. Площадь трапеции: S =  ; a,b – стороны; h – высота
4. Площадь шестиугольника: S6 = 15,48; R – радиус описанной окружности
; a,b – стороны; h – высота
4. Площадь шестиугольника: S6 = 15,48; R – радиус описанной окружности





