
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Індивідуальні завдання за темою: «Лінійна алгебра»Содержание книги
Поиск на нашем сайте
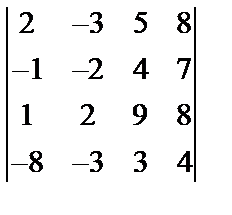
Завдання №1
Завдання №2
Завдання № 3
Задані дві матриці А і В. Знайти: а) (2А-В); б) АВ; в) ВА; г)
2.1 2.2 2.3 2.4 2.5 2.6
2.7 2.8 2.9 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 2.27 2.28 2.29 2.30 Індивідуальні завдання за темою: «Елементи векторної алгебри та аналітичної геометрії» Завдання1 Дано координати вершин трикутної піраміди
Знайти: 1) Довжину ребра
2) Кут між ребрами 3) Кут між ребрами 4) Площу грані 5) Об’єм піраміди; 6) Абсцису та аплікату т. 7) Відстань від точки 8) Написати рівняння площини,що проходить через точку 9) Роботу рівнодіючої двох сил 10) Координати вектора – моменту сили ВАРІАНТИ
Завдання №2 Дано прямі l1, l2 та точка М0(x0;y0). Потрібно: 1) Записати рівняння прямої l1 у відрізках на осях, а прямої l2 з кутовим коефіцієнтом. Зобразити ці прямі геометрично; 2) Написати рівняння прямої l3, що проходить через точку М0(x0;y0) паралельно прямій l1. 3) Знайти відстань між прямими l2 та l3. 4) Написати рівняння прямої l4, що проходить через точку М0(x0;y0) перпендикулярно прямий l2. 5) Обчислити косинус кута між прямими l1 та l2. 6) Написати рівняння прямої l5, яка проходить через точку М0(x0;y0) та точку перетину прямих l1 і l2. 7) Написати рівняння прямої l6, що проходить через точку М0(x0;y0) і відсікає від координатного кута трикутник, площа якого дорівнює 12 кв.од.
Задача № 3. Привести до канонічного вигляду лінії другого порядку, зробити малюнок
Індивідуальні завдання за темою: «Диференціальне числення функції однієї змінної»
ВИБІР ВАРІАНТУ
Умови до завдань 1,2,3 кожного завдання вибираються відповідно до перших трьох букв прізвища; умови до завдань 4,5,6 – першими трьома буквами імені; умови до завдань 7,8,9 – першими трьома буквами побатькові.
ТАБЛИЦЯ 1 – До вибору номера завдання.
Примітка: Якщо при виборі номера зустрічається буква «ь» (м’який знак), то замість неї слід узяти наступну букву. Приклад: Студент ІВА НОВ СЕР ГІЙ ПЕТР ОВИЧ 931 766 5686
Завдання №1
Обчислити границі.
Варіанти: №1.
а)
в)
д)
№2
в)
д)
№3
а)
в)
д)
№4. а)
в)
д)
№5. а)
в)
д)
№6. а)
в)
д)
№7 а)
в)
д)
№8. а)
в)
д)
№9. а)
в)
д)
№10.
а)
в)
д)
Завдання №2
Для даної функції а) знайти точки розриву; б) класифікувати точки розриву, визначити їх тип; в) зробити креслення
Варіанти: №1. №3.
№5.
№7.
№9.
Завдання №3
Задані функції однієї змінної. Необхідно: а),б) знайти похідну функції в) обчислити значення похідної функції г) знайти диференціал функції
Варіанти:
№1. а) в)
№2. а) в)
№3. а) в)
№4. а) в)
№5. а) в)
№6. а) в)
№7. а) в)
№8. а) в)
№9. а) в)
№10. а) в)
Завдання №4
Скласти рівняння дотичної до даної кривої в крапці з абсцисою
Варіанти:
№1.
№3.
№5.
№7.
№9. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

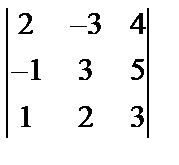

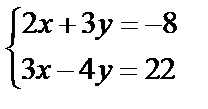

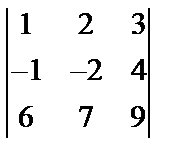



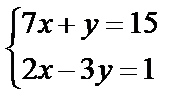
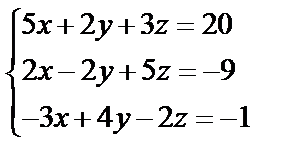
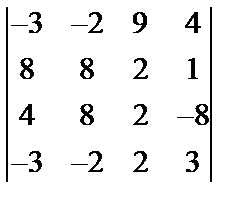


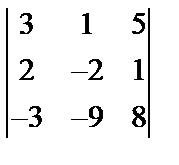

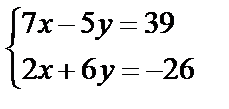



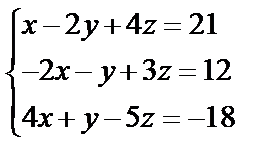
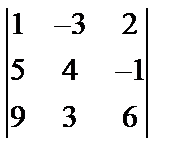
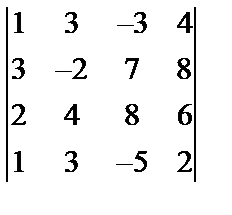
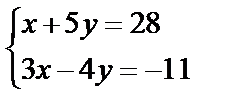

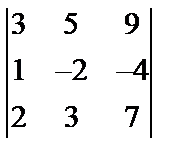

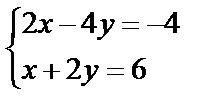

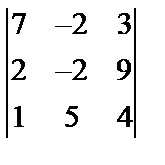
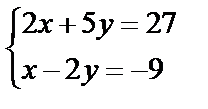
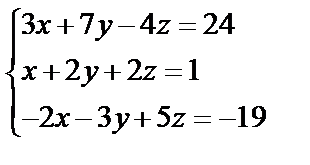
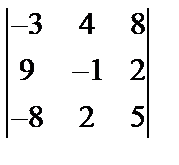
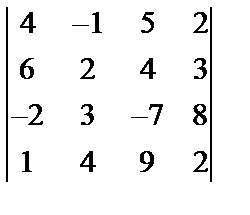

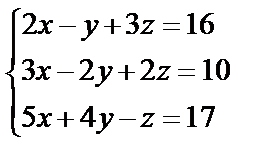

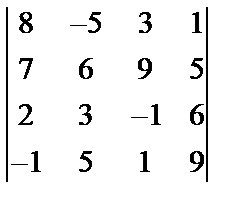
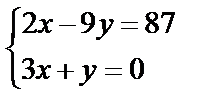


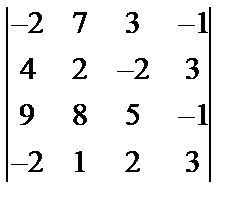
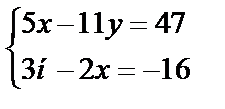
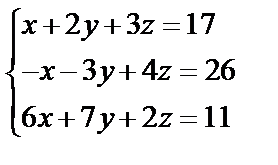


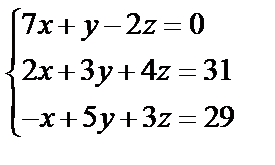
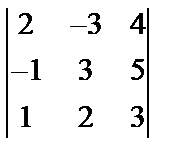
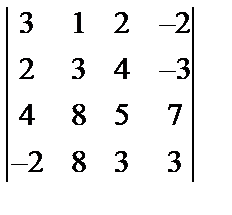
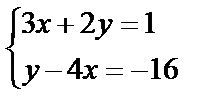
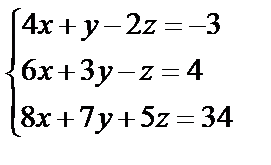





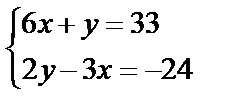
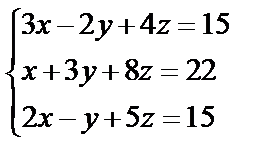
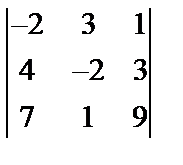
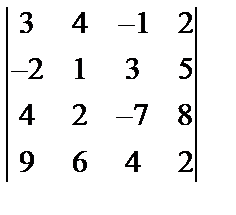

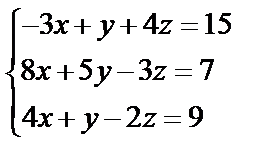
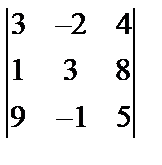
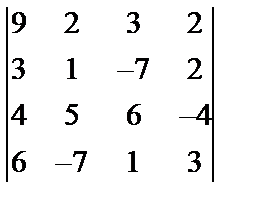

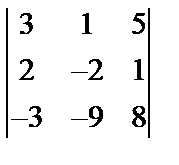
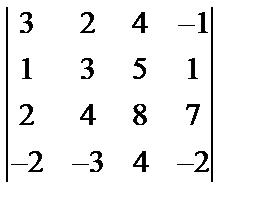
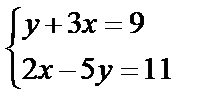
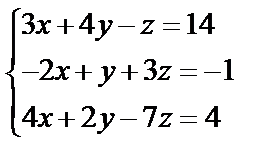
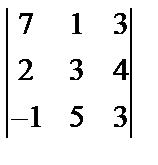

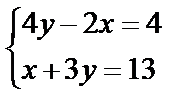

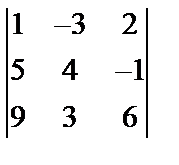
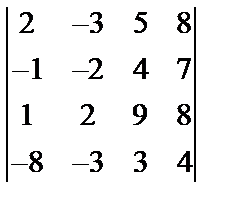
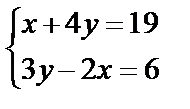
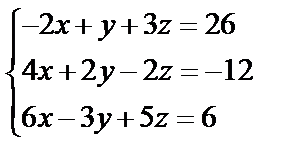


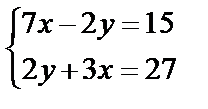
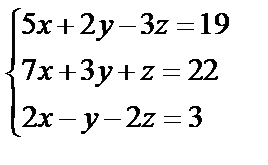
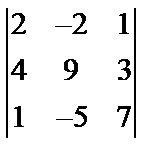
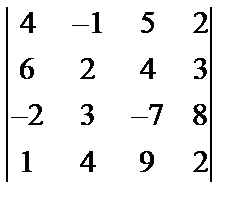
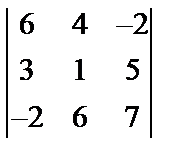
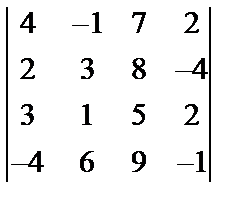
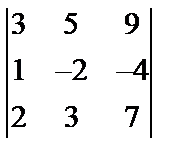
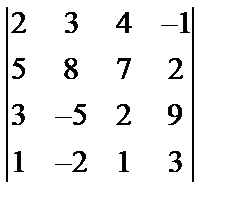
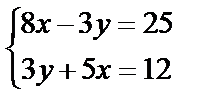

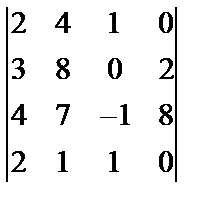
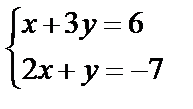
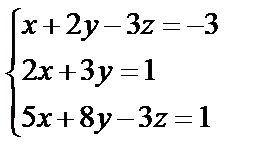
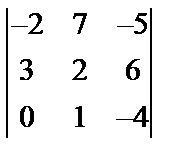
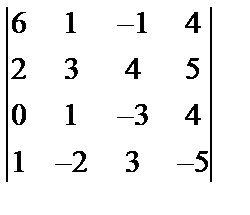
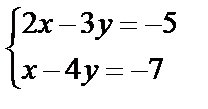

 ,
, 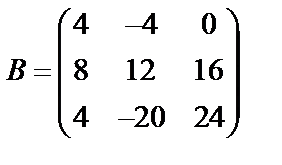

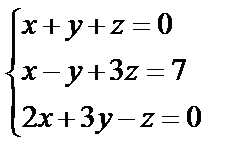
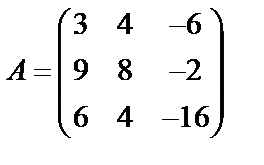 ,
, 

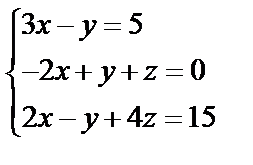
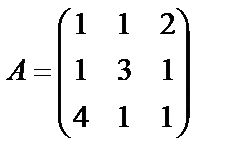 ,
, 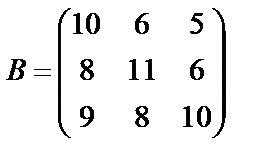
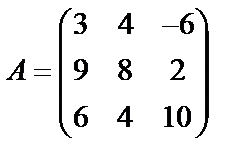
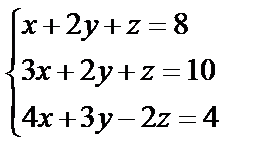
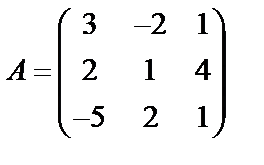 ,
, 
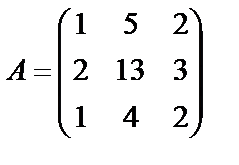

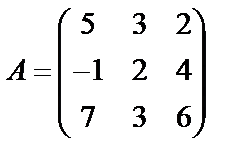 ,
, 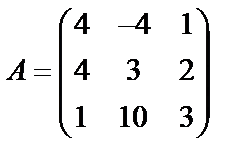
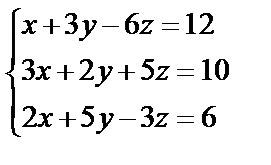
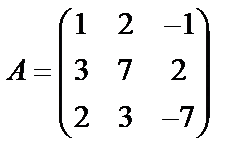 ,
, 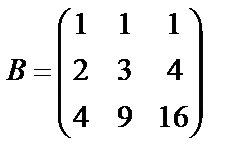
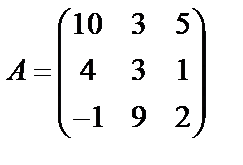
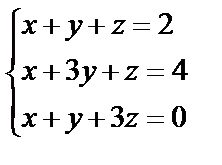
 ,
, 

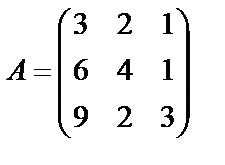 ,
, 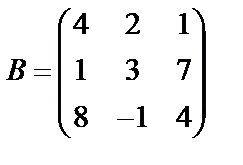

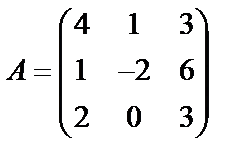 ,
, 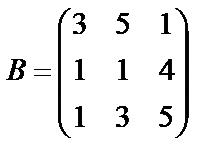
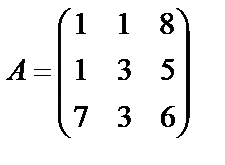

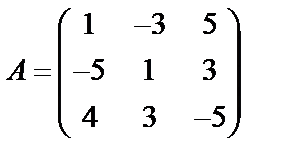 ,
, 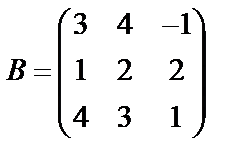
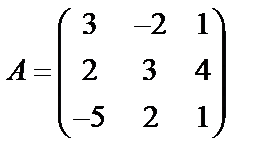
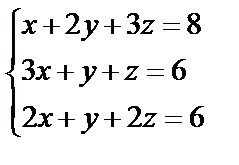
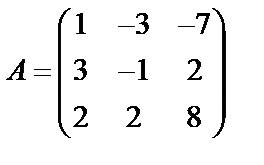 ,
, 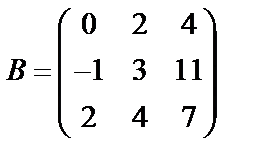

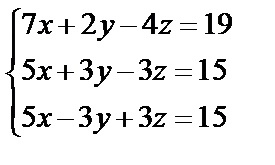
 ,
, 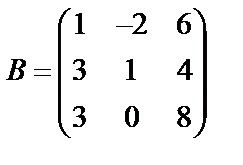
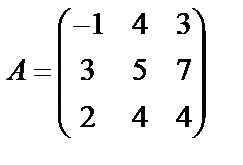
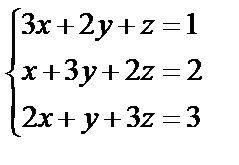
 ,
, 
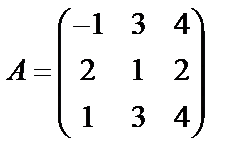
 ,
, 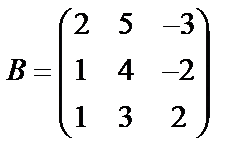
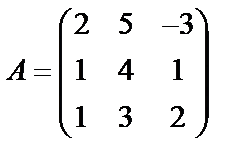

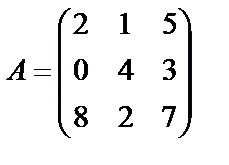 ,
, 
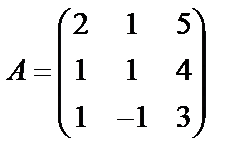

 ,
, 
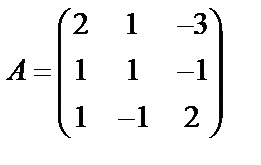

 ,
, 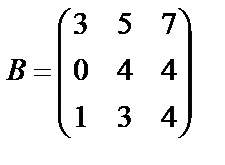
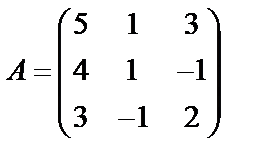
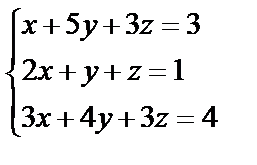
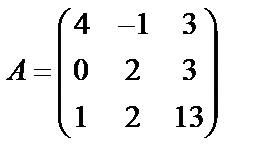 ,
, 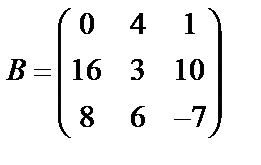
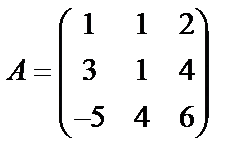
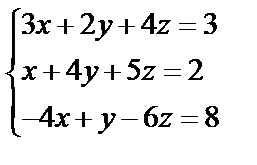

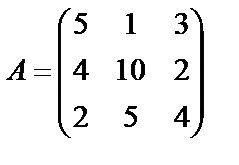
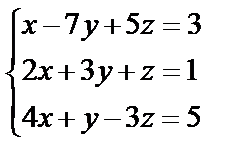
 ,
, 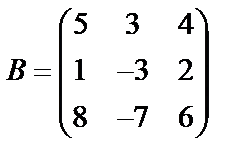
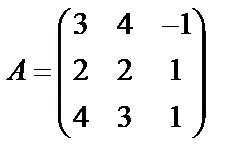
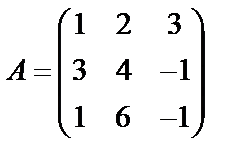 ,
, 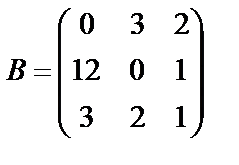

 ,
, 
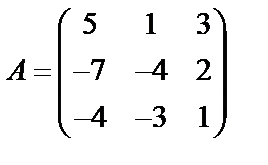
 ,
, 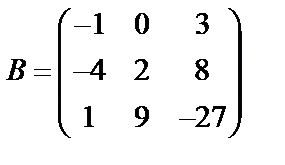
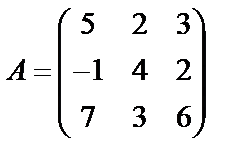
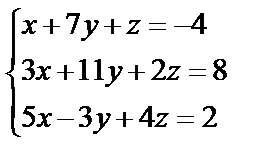
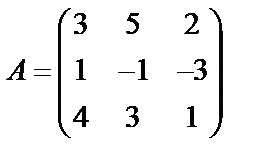 ,
, 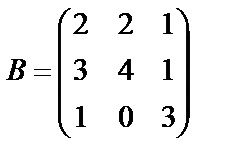
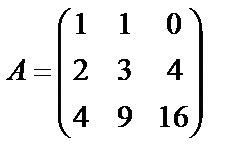
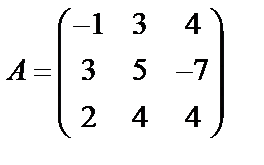 ,
, 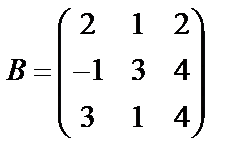
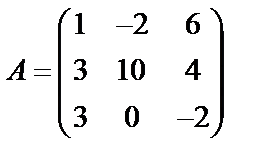
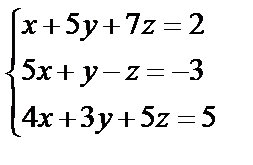
 ,
, 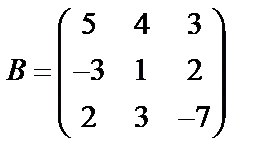

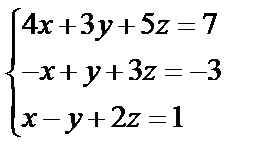
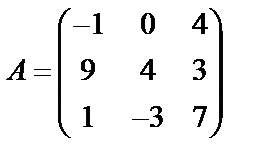 ,
, 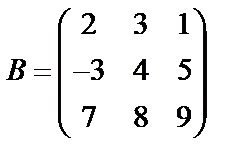
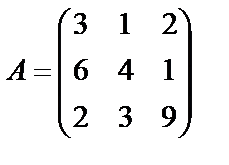
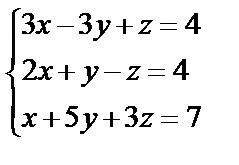
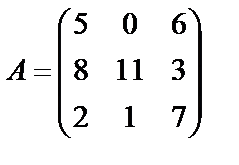 ,
, 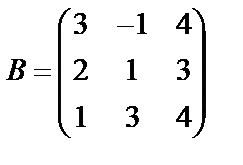
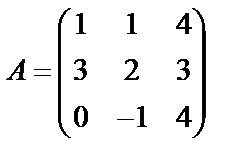

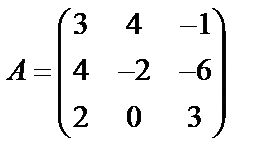 ,
, 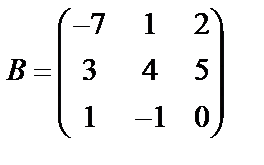
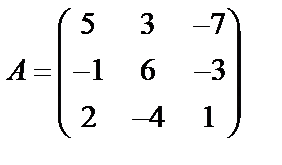
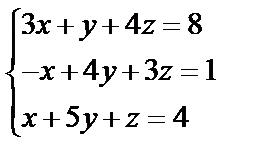
 ,
, 


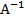 д)
д) 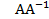 .
.
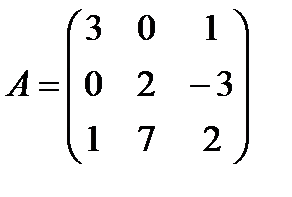
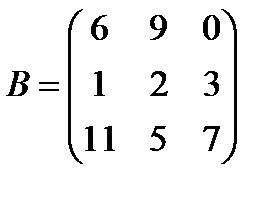
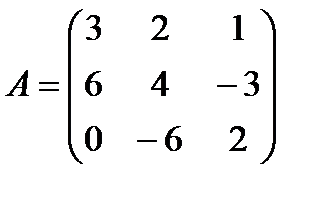

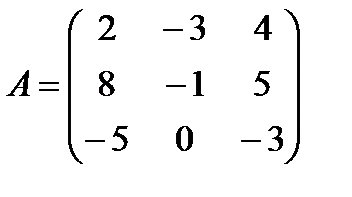
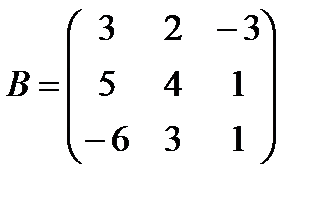
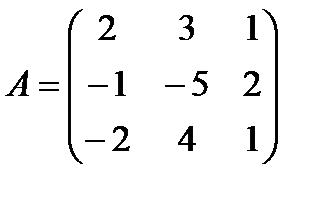

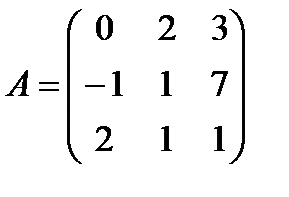
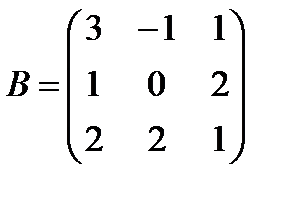
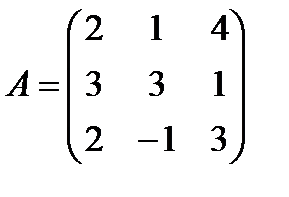

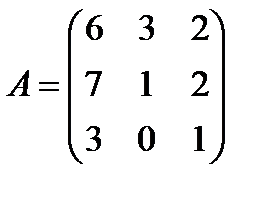
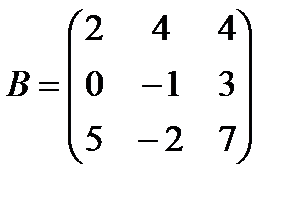
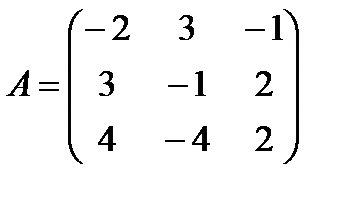
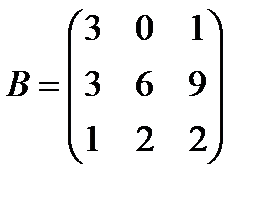

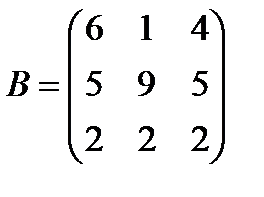
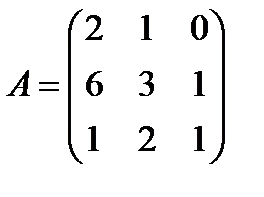
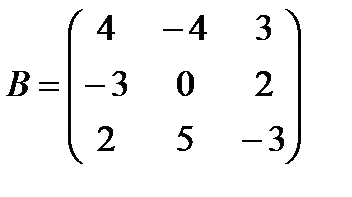




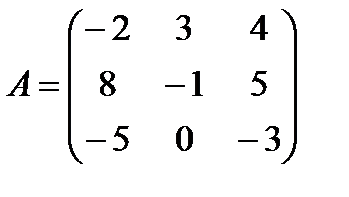
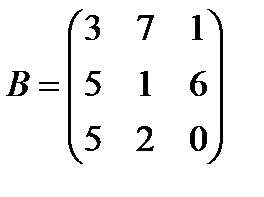
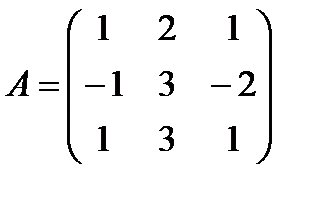
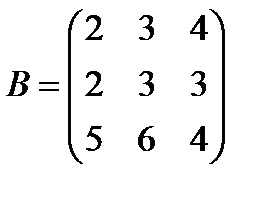
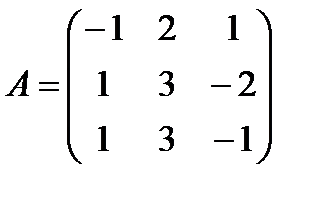
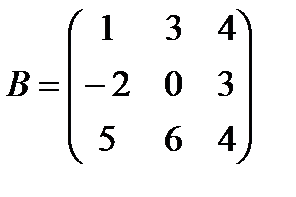
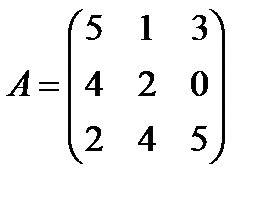

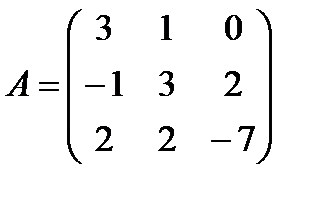
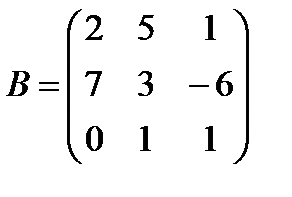

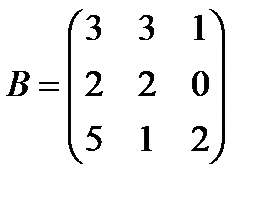
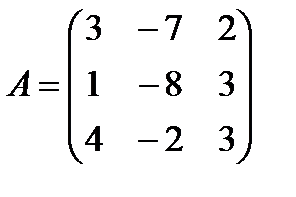
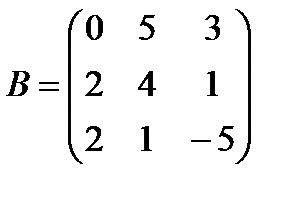
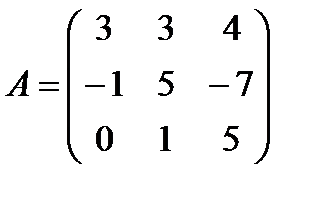

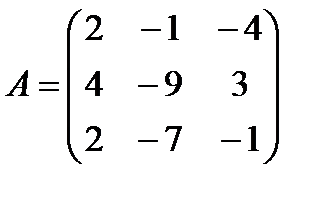
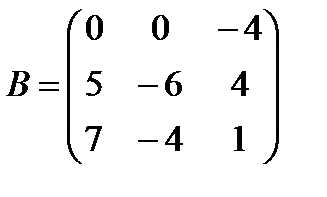
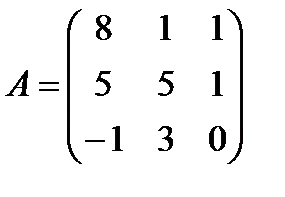
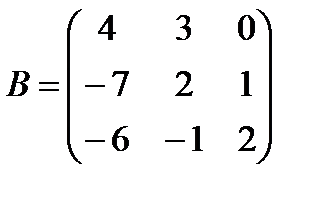

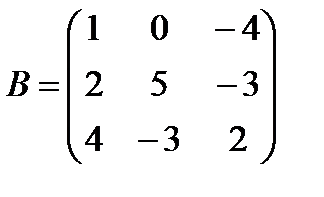
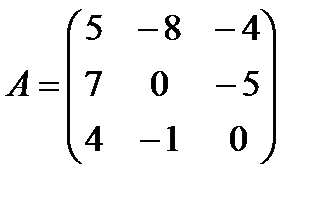
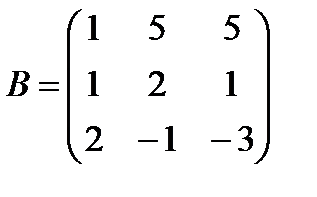
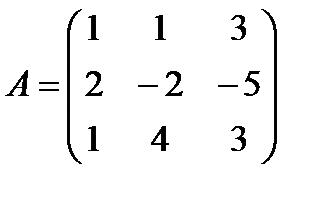
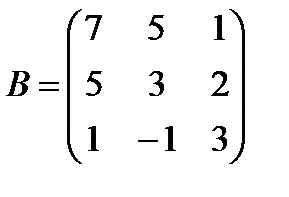

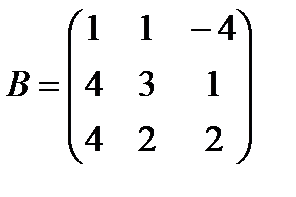

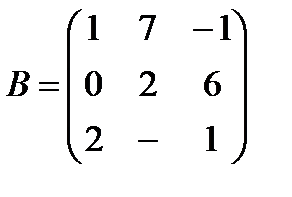

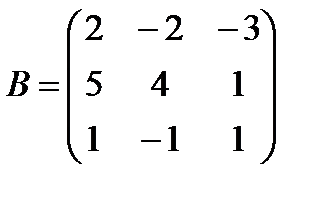


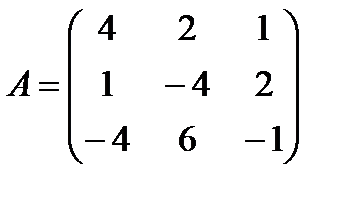



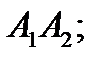
 і
і 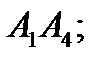
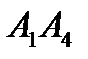 і гранню
і гранню 
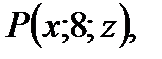 що належить висоті
що належить висоті 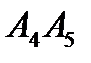 опущеної з вершини
опущеної з вершини 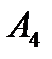 на грань
на грань 
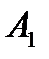 - до площини,що проходить через три точки
- до площини,що проходить через три точки 
 перпендикулярно вектору
перпендикулярно вектору 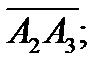
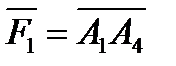 та
та 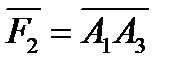 при прямолінійному переміщені матеріальної точки з положення
при прямолінійному переміщені матеріальної точки з положення  у положення
у положення 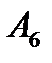 - точку,що поділяє відрізок
- точку,що поділяє відрізок 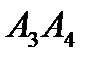 у відношенні 2:1,відраховуючи від т.
у відношенні 2:1,відраховуючи від т. 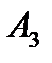 до т.
до т. 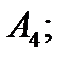
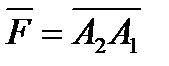 ,прикладеної до точки
,прикладеної до точки  відносно точки
відносно точки 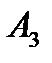 та його величину.
та його величину.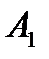

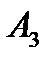
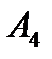
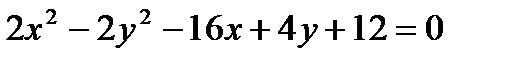
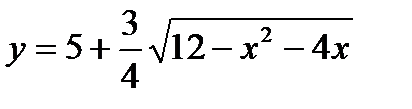
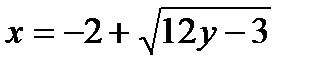
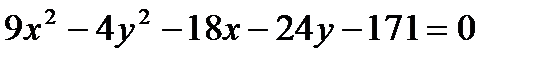
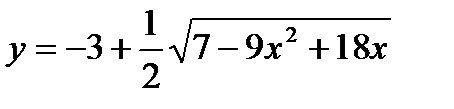
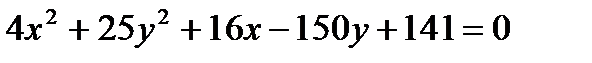
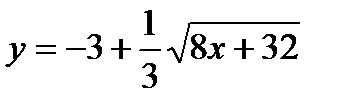

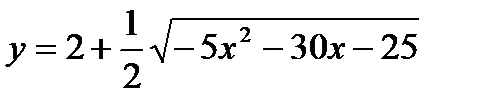
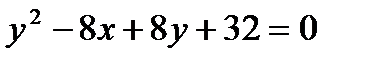
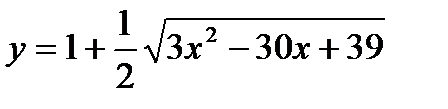

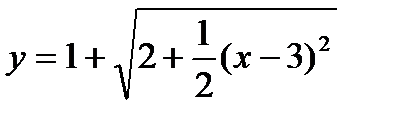

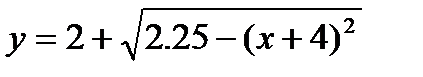


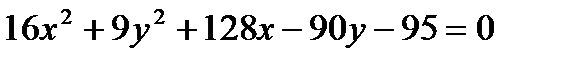


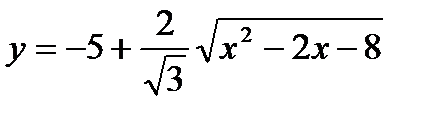



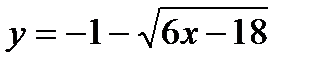

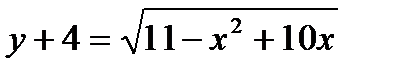
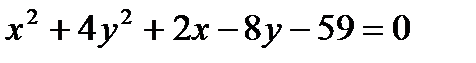
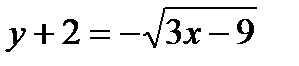
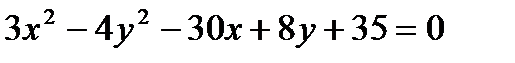
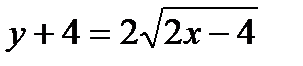

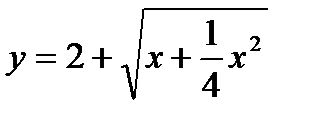
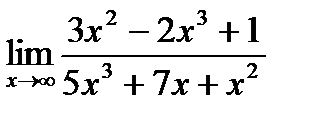 ; б)
; б) 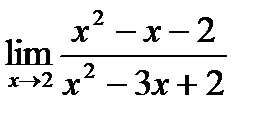 ;
;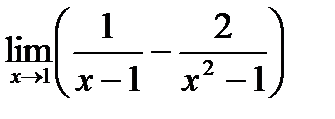 ; г)
; г) 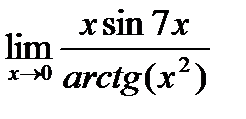 ;
;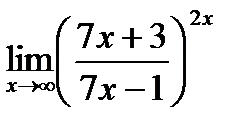 ;
;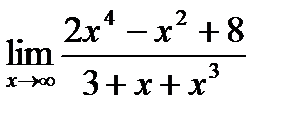 ; б)
; б) 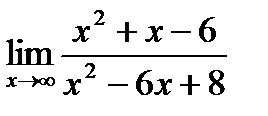 ;
;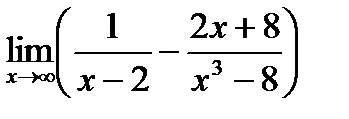 ; г)
; г)  ;
;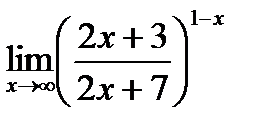 ;
;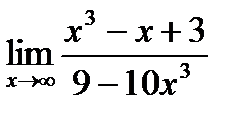 ; б)
; б) 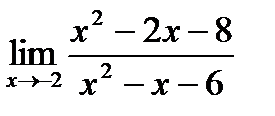 ;
; ; г)
; г) 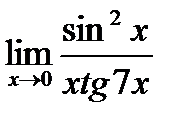 ;
; ;
;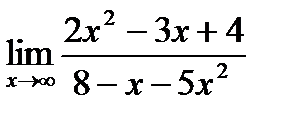 ; б)
; б) 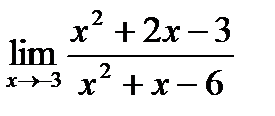 ;
;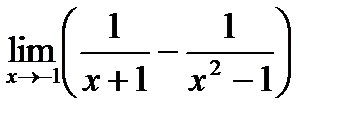 ; г)
; г) 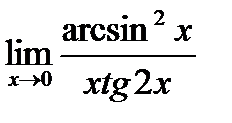 ;
;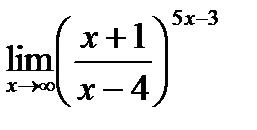 ;
;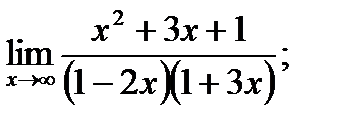 б)
б) 
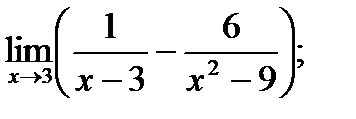 г)
г) 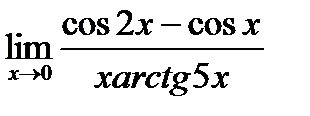 ;
;
 б)
б) 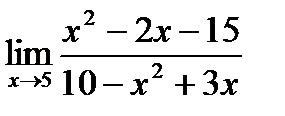 ;
;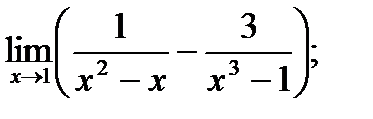 г)
г) 
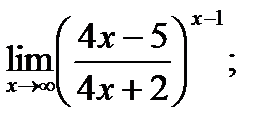
 б)
б) 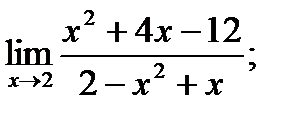
 г)
г) 
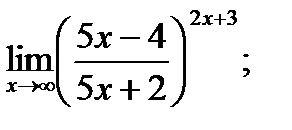
 б)
б) 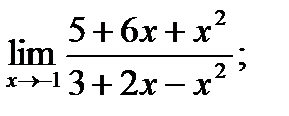
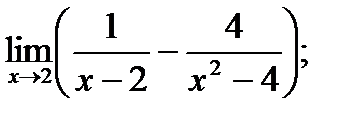 г)
г) 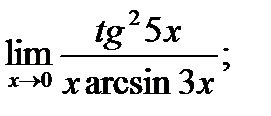

 б)
б) 
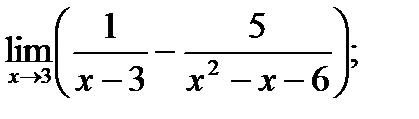 г)
г) 
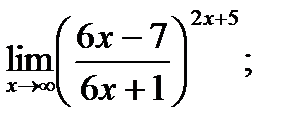
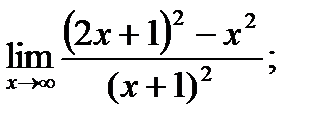 б)
б) 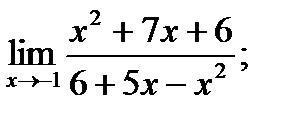
 г)
г) 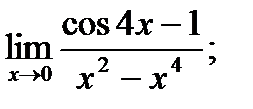
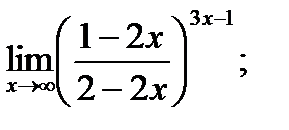
 необхідно:
необхідно: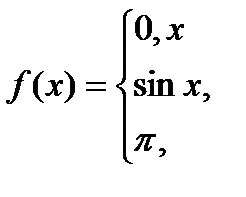
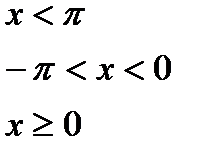 №2.
№2. 


 №4.
№4. 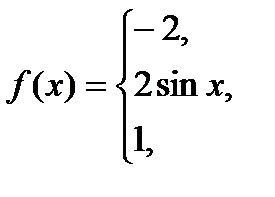
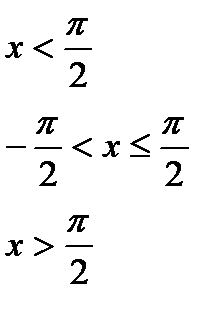

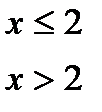 № 6.
№ 6. 
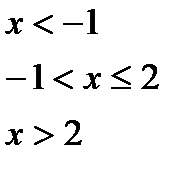

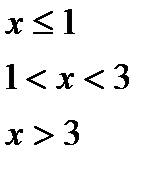 №8.
№8. 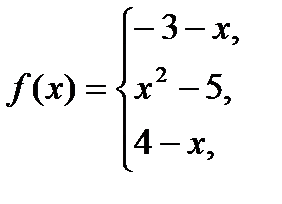
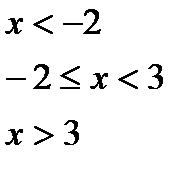
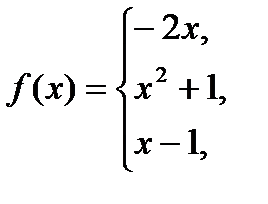
 №10.
№10. 
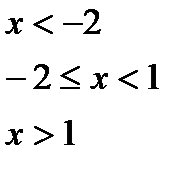
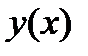 ;
;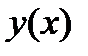 в точці
в точці 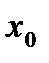 ;
;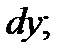
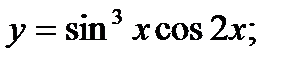 б)
б) 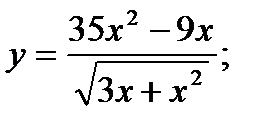
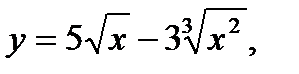
 ; г)
; г) 
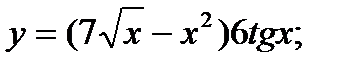 б)
б) 
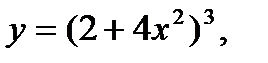
 г)
г) 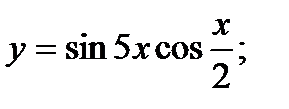
 б)
б) 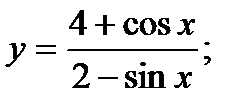

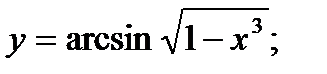
 б)
б) 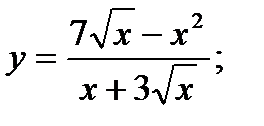
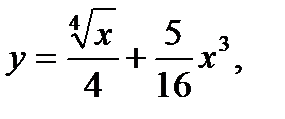

 б)
б) 
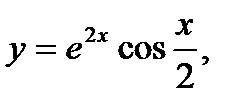
 г)
г) 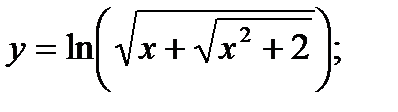
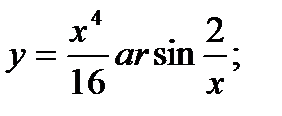 б)
б) 
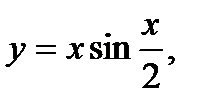
 г)
г) 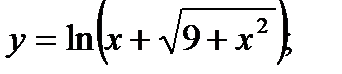
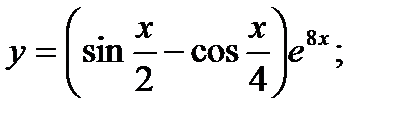 б)
б) 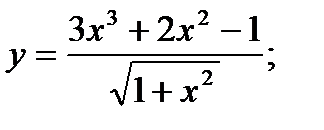


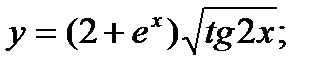 б)
б) 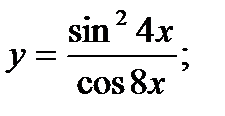

 г)
г) 
 б)
б) 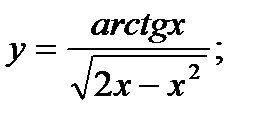
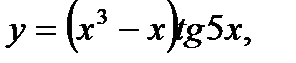
 г)
г) 
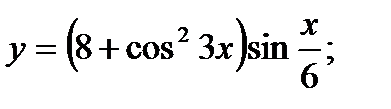 б)
б) 
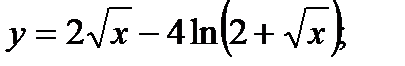
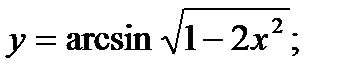
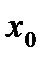 .
.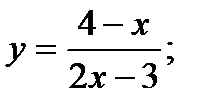
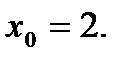 №2.
№2. 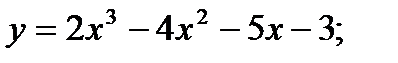
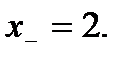
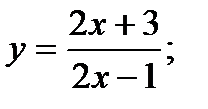
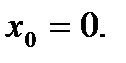 № 4.
№ 4. 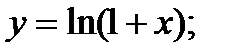
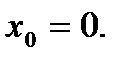
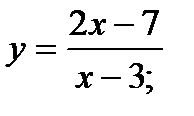
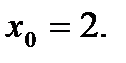 №6.
№6. 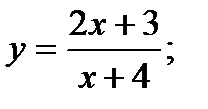
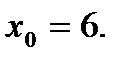
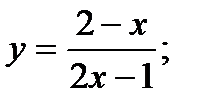
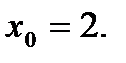 №8.
№8. 
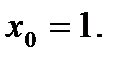

 №10.
№10. 


