
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поясніть принципи динамічного створення елементів інтерфейсу Delphi.Содержание книги
Поиск на нашем сайте
Складні проекти мають багато режимів своєї роботи причому кожен з цих режимів має десятки своїх компонент на вікні форми. І під час візуального програмування на вікні форми розмістити їх фізично неможливо. Тому ми будемо формувати компоненти динамічно. Для створення компонентів під час програми необхідно виконати такі дії: - Створити екземпляр класу за допомогою конструктора Create, передавши, при необхідності силку на компонент, який буде нести відповідальність за руйнування створюваного компонента. Якщо компонент буде зруйнований (звільнений) в тексті програми, то силку можна не передавати, використавши значення nil - Для візуальних компонентів встановити властивість Parent, присвоївши йому силку на контейнер, в якому буде відображатися створюваний компонент - Для візуальних компонентів встановити властивості, яка визначає положення, розміри та інші необхідні візуальні характеристики елементів управління - При необхідності реалізувати у вигляді методів будь-якого класу і призначити компоненті обробники подій - Якщо при створенні компонента не був указаний власник Owner, зруйнувати (звільнити) компоненту, викликавши його метод Free. Якщо компонент має власника, то він буде звільнений автоматично.
Динамічні масиви, синтаксис оголошення та правила використання. Масив – це впорядкований набір даних, як правило кількість елементів обмежена. Масиви бувають статичні та динамічні. Номери елементів наз. індексами. Тип компонентів наз. базовим типом(крім файлового). Кожна компонента моє свій індекс. Всі компоненти мають один і той самий тип. Статичні: var <ім’я масиву>:array[<діапазон> <вимірність>] of < тип елементів масиву>; статичні масиви мають недолік. В більшості випадків ми не знаємо скільки елементів нам потрібно. Динамічні масиви не мають фіксованого розміру або довжини Var MyArray: array of real; В такому оголошенні пам’яті не виділяється. Для виділення пам’яті для динамічного масиву використовується процедура: SetLength (MyArray,100) Тобто масиву MyArray задається довжина 100, індексування від 0. Динамічні масиви – це неявні вказівники. Щоб звільнити пам’ять, яку займає динамічний масив потрібно масиву присвоїти nil: MyArray:=nil; Щоб оголосити двомірний масив: Var MyArray: array of array of integer; Для виділення пам’яті: SetLength (MyArray,10,5); Працювати з двовимірними масивами так само як із статичними. Ми можемо створювати не тільки прямокутні масиви. Зубчасті масиви Var MyArray: array of array of integer; Потім створимо n рядків але без колонок, наприклад: SetLength (MyArray,n); Тепер можна створити стовпці різної довжини: SetLength (MyArray[0],5); SetLength (MyArray[1],8); SetLength (MyArray[2],4); 41. Метод Ньютона для розв’язання СНАР(теорія). Найпростішим ітераційним методом розв’язування системи нелінійних рівнянь є метод простої ітерації. Одним з найпотужніших є метод Ньютона. Припустимо, що система має принаймні 1 розв’язок, тобто існує такий вектор Х* , підстановка якого у кожне з рівнянь системи перетворює це рівняння в тотожність. Головна ідея цього методу полягає у вилученні з рівнянь лінійних частин, які є головними за малих приростів аргументів. Такий крок дає змогу звести початкову задачу до розв’язання послідовності лінійних систем. Метод Ньютона для N рівнянь можна застосовувати тільки тоді, коли можна обчислити всі частинні похідні функції fi за змінними xi. Ja(X) – матриця частинних похідних вектора F по змінних X. Таку матрицю називають матрицею Якобі. Її (i,j)-м елементом є значення похідної. F(X) X(k+1)=X(k)-Ja-1(X(k))*F(X(k)) – формула ітераційного методу. K – номер ітерації. Dx(k)= Ja-1(X(k))*F(X(k)) Вектор Dx(k) називають вектором нев’язки. Ja-1(X(k))*Dx(k)= F(X(k)) – цей вираз є системою лінійних алгебраїчних рівнянь щодо вектора невідомих Dx(k). Розв’язавши цю систему методом Гауса, використаємо її розв'язок в ітераційному процесі Ньютона: X(k+1)=X(k)- Dx(k). Елементи матриці Якобі визначаються:
Q – малий приріст змінної, який доцільно вибирати таким:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.38 (0.008 с.) |

 xi
xi 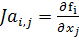 .
. F(X(0))+Ja(X(0))*(X-X(0)) – ф-я в ряд Тейлора
F(X(0))+Ja(X(0))*(X-X(0)) – ф-я в ряд Тейлора




