
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра летательных аппаратовСодержание книги
Поиск на нашем сайте
Кафедра летательных аппаратов
Курсовая работа По строительной механике
Вариант 7
Выполнила: студентка гр. Н-20 Головина А.С.
Таганрог 2012 Содержание
Расчет стержневых систем………………………………………………………..3
Расчет подкрепленных тонкостенных конструкций по балочной теории…14
Расчет тонкостенных консольных балок……………………………………..23 Расчет стержневых систем Рассчитать пространственную ферму типа полурамы двигателя Требуется: А) установить геометрическую неизменяемость и статическую неопределимость системы; Б) определить усилия в стержнях фермы при заданных значениях E и F; В) найти перемещение узла.
Исходные данные:
Направление перемещения узла 1 – вдоль оси ОХ.
Решение: 1. Определение геометрической неизменяемости и степени статической неопределимости системы. Данная система стержней представляет собой ферму 1-2-3-4, присоединенную семью стержнями к шарнирным опорам. Данная ферма является пространственной. Для установления геометрической неизменяемости воспользуемся способом разрушения: отбросим узел 1, относительная неподвижность которого обеспечена тремя стержнями 1-2, 1-3, 1-4, не лежащими в одной плоскости. Остается пространственная ферма 2-3-4. Вся пространственная ферма 1-2-3-4 присоединена к опорам семью стержнями 1-6, 3-6, 2-7, 3-9, 3-8, 4-5 и 4-8, любые 6 из которых не пересекают одну ось. Отсюда следует, что данная система геометрически неизменяема, причем один из семи крепящих стержней лишний, т.е. система один раз статически неопределима, что подтверждается формулой
где
1. Определение усилия в стержнях фермы. Для этого отбросим любой из крепящих стержней, например 1-6. Получили статически определимую систему под действием внешних нагрузок P и G. Это система «Р». Решим ее методом вырезания узлов, предварительно заполнив таблицу
Составляем уравнения равновесия для узла 1:
или
Решение этой системы методом Крамера дает
Вырезаем узел 2 и составляем уравнения равновесия:
или
Решение этой системы методом Крамера дает
Вырезаем узел 4 и составляем уравнения равновесия:
или
Решение этой системы методом Крамера дает
Вырезаем узел 3 и составляем уравнения равновесия:
или
Решение этой системы дает
Итак, в системе «Р» действуют следующие нагрузки:
Рассмотрим систему «1»: заменяем стержень 1-6 единичной продольной силой Т, направленной по оси Y, и отбрасываем силы P и G. Систему «1» решаем методом вырезания узлов.
Рассмотрим узел 1.
или
Решением этой системы уравнений являются следующие усилия:
Рассмотрим узел 2:
или
Решение этой системы дает
Переходим к узлу 4
или
Решение этой системы дает
Переходим к узлу 3:
или
Решение этой системы дает следующие результаты:
Итак, в системе «1» действуют следующие усилия в стержнях:
;
Составляем каноническое уравнение для нахождения реакции
где
Решая каноническое уравнение получаем:
Теперь определим реально действующие усилия в стержнях:
Находим перемещения узла 3 в направлении оси ОХ.
Перемещение определяется по формуле
где
Теперь найдем
или
Решением этой системы уравнений являются следующие усилия:
Рассмотрим узел 2:
или
Решением данной системы уравнений являются следующие усилия:
Переходим к узлу 4
или
Решением этой системы уравнений являются следующие усилия:
Вырезаем узел 3, к которому приложена единичная нагрузка в направлении оси ОХ
или
Решение этой системы дает следующие результаты:
Итак, усилия в системе «1» следующие:
Теперь находим перемещение узла 3:
Определение суммарного ПКС Суммарный ПКС определяю по формуле (1), эпюра представлена на рисунке Расчёты ПКС приведены в приложении 2, результаты сведены в таблицу 2
Решение Кафедра летательных аппаратов
Курсовая работа По строительной механике
Вариант 7
Выполнила: студентка гр. Н-20 Головина А.С.
Таганрог 2012 Содержание
Расчет стержневых систем………………………………………………………..3
Расчет подкрепленных тонкостенных конструкций по балочной теории…14
Расчет тонкостенных консольных балок……………………………………..23 Расчет стержневых систем Рассчитать пространственную ферму типа полурамы двигателя Требуется: А) установить геометрическую неизменяемость и статическую неопределимость системы; Б) определить усилия в стержнях фермы при заданных значениях E и F; В) найти перемещение узла.
Исходные данные:
Направление перемещения узла 1 – вдоль оси ОХ.
Решение: 1. Определение геометрической неизменяемости и степени статической неопределимости системы. Данная система стержней представляет собой ферму 1-2-3-4, присоединенную семью стержнями к шарнирным опорам. Данная ферма является пространственной. Для установления геометрической неизменяемости воспользуемся способом разрушения: отбросим узел 1, относительная неподвижность которого обеспечена тремя стержнями 1-2, 1-3, 1-4, не лежащими в одной плоскости. Остается пространственная ферма 2-3-4. Вся пространственная ферма 1-2-3-4 присоединена к опорам семью стержнями 1-6, 3-6, 2-7, 3-9, 3-8, 4-5 и 4-8, любые 6 из которых не пересекают одну ось. Отсюда следует, что данная система геометрически неизменяема, причем один из семи крепящих стержней лишний, т.е. система один раз статически неопределима, что подтверждается формулой
где
1. Определение усилия в стержнях фермы. Для этого отбросим любой из крепящих стержней, например 1-6. Получили статически определимую систему под действием внешних нагрузок P и G. Это система «Р». Решим ее методом вырезания узлов, предварительно заполнив таблицу
Составляем уравнения равновесия для узла 1:
или
Решение этой системы методом Крамера дает
Вырезаем узел 2 и составляем уравнения равновесия:
или
Решение этой системы методом Крамера дает
Вырезаем узел 4 и составляем уравнения равновесия:
или
Решение этой системы методом Крамера дает
Вырезаем узел 3 и составляем уравнения равновесия:
или
Решение этой системы дает
Итак, в системе «Р» действуют следующие нагрузки:
Рассмотрим систему «1»: заменяем стержень 1-6 единичной продольной силой Т, направленной по оси Y, и отбрасываем силы P и G. Систему «1» решаем методом вырезания узлов.
Рассмотрим узел 1.
или
Решением этой системы уравнений являются следующие усилия:
Рассмотрим узел 2:
или
Решение этой системы дает
Переходим к узлу 4
или
Решение этой системы дает
Переходим к узлу 3:
или
Решение этой системы дает следующие результаты:
Итак, в системе «1» действуют следующие усилия в стержнях:
;
Составляем каноническое уравнение для нахождения реакции
где
Решая каноническое уравнение получаем:
Теперь определим реально действующие усилия в стержнях:
Находим перемещения узла 3 в направлении оси ОХ.
Перемещение определяется по формуле
где
Теперь найдем
или
Решением этой системы уравнений являются следующие усилия:
Рассмотрим узел 2:
или
Решением данной системы уравнений являются следующие усилия:
Переходим к узлу 4
или
Решением этой системы уравнений являются следующие усилия:
Вырезаем узел 3, к которому приложена единичная нагрузка в направлении оси ОХ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


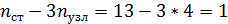 ,
,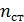 – число стержней системы;
– число стержней системы; – число узлов, не являющихся опорными.
– число узлов, не являющихся опорными.
 ;
; ;
; ,
, ;
; ;
; ,
, ;
;  ;
;  .
.
 ;
;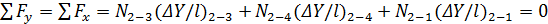 ;
; ,
,
 ;
;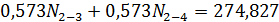 ;
; .
. ;
;  ;
;  .
.
 ;
; ;
; ,
,
 ;
; ;
; .
.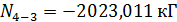 ;
;  ;
;  .
.
 ;
; ;
; ,
,
 ;
;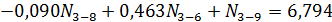 ;
; .
. ;
;  ;
;  .
.

 ;
; ;
; ,
,
 ;
; .
. ;
; 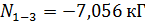 ;
;  .
.
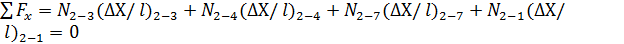 ;
;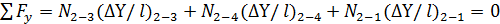 ;
; ,
, ;
; ;
; .
. ;
;  ;
;  .
.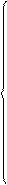
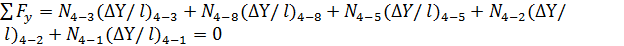 ;
; ;
; ;
; .
. ;
; 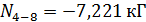 ;
;  .
.
 ;
; ;
; .
.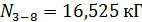 ;
;  ;
;  .
.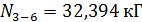 ;
;  стержня 1-6
стержня 1-6 ,
, – перемещение узла 1 в направлении единичной силы от внешних сил:
– перемещение узла 1 в направлении единичной силы от внешних сил: – перемещение от единичной силы в направлении реакции;
– перемещение от единичной силы в направлении реакции;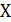 – реакция связи (стержня 1-6).
– реакция связи (стержня 1-6). ;
; .
.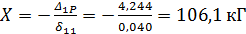 .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;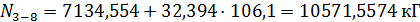 ;
; .
.
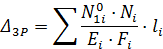
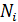 – действительные усилия в стержнях системы;
– действительные усилия в стержнях системы; – усилия от единичной нагрузки, приложенной в узле 3, в направлении оси ОХ при отброшенных силах P и G.
– усилия от единичной нагрузки, приложенной в узле 3, в направлении оси ОХ при отброшенных силах P и G.
 ;
;
 ,
,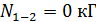 ;
; 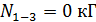 ;
;  ;
;

 ;
;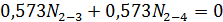 ;;
;; .
. ;
;  ;
;  .
.
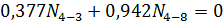 ;
;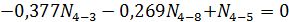 ;
; .
. ;
;  ;
;  ;
;

 ;
; ;
; .
. ;
;  ;
;  .
. ;
; 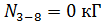 ;
; 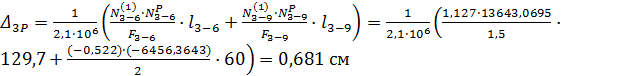 .
.








